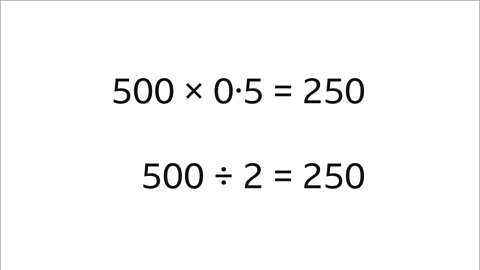What Is A Geometric Sequence? - BBC Bitesize

Home » What Is The Common Ratio » What Is A Geometric Sequence? - BBC Bitesize

Maybe your like

  1. Key points
  2. Finding missing terms
    1. Examples
    2. Question
  3. Finding the common ratio
    1. Examples
    2. Question
  4. Practise geometric sequences
    1. Quiz
  5. Real-life maths

Key points

Image caption, Each term in this sequence is doubling (multiplying by 2) to create the next term.

A sequence is a list of numbers or diagrams that are in order.

  • Number sequences are sets of numbers that follow a pattern or a rule.

  • If the rule is to multiply or divide by a specific number each time, it is called a geometric sequence.

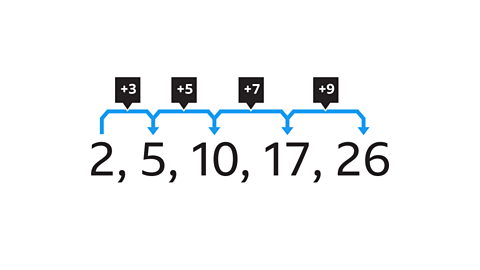
  • A number pattern which increases (or decreases) by the same amount each time is called an arithmetic linear sequence.

  • Recognising the pattern between the terms means that the sequence can be continued using a term-to-term rule.

  • Sequences that are connected by multiplicative relationships are geometric sequences, whereas those connected by additive relationships are linear.

Image caption, Each term in this sequence is doubling (multiplying by 2) to create the next term.
Back to top

Finding missing terms in a geometric sequence

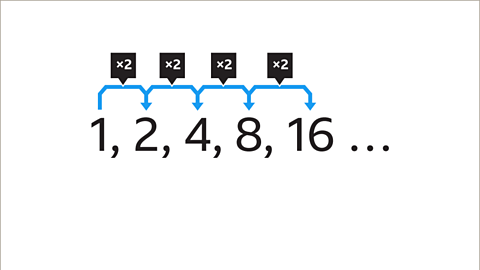
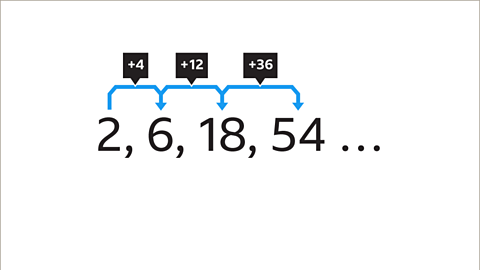
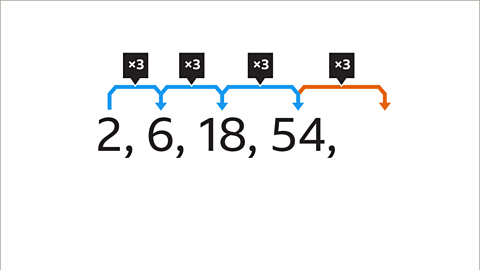
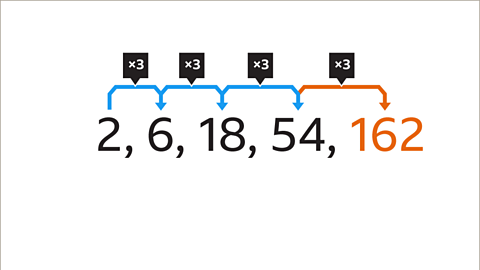
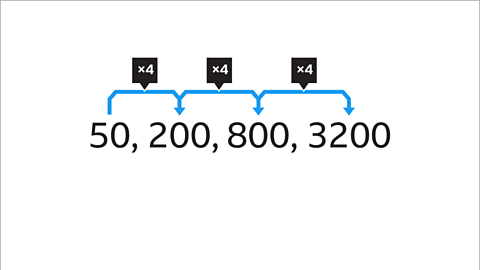
  • Each term in a geometric sequence is found by multiplying or dividing the previous term by the same amount, this is called the common ratio.

  • To find the common ratio, start by calculating the difference between each pair of numbers, moving from one term to the next.

Examples

Image gallerySkip image gallery
  1. Example one. A sequence with the terms one, two, four, eight, sixteen.
    Image caption,

    What is the next term in the sequence?

1 of 9

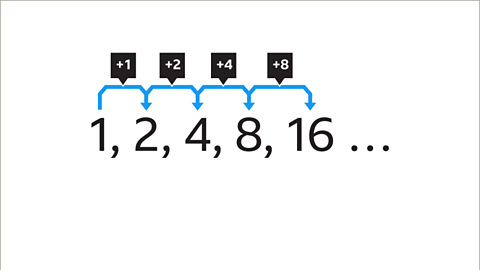
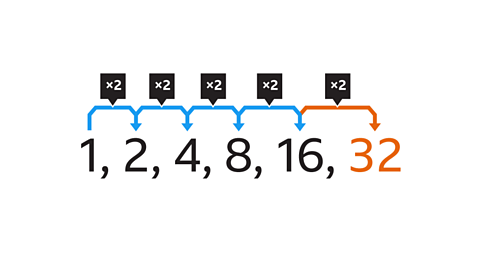
Previous imageNext imageSlide 1 of 9, Example one. A sequence with the terms one, two, four, eight, sixteen., What is the next term in the sequence?End of image gallery

Question

What is the next number in this geometric sequence?

A sequence with the terms eighty, forty, twenty, ten.

Show answer

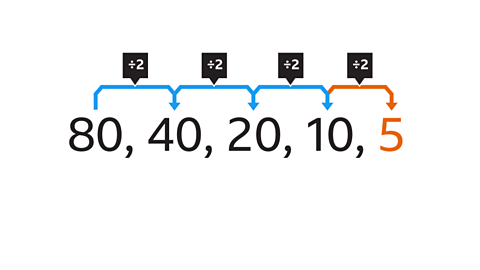
The same sequence as the previous. Written above: between each pair of terms is the common ratio. Divide by two, divide by two, divide by two, with curved arrows going from left to right coloured blue. Written right: Divide by two with an orange arrow. The next term in the sequence, five, has been written in orange.

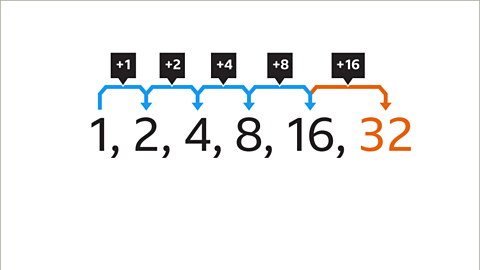
  • Each term in the sequence is divided by 2 to create the next term.

  • The next term in the sequence is found by dividing the previous term (10) by 2

  • 10 ÷ 2 = 5

  • 5 is the next number in this geometric sequence.

Back to top

Finding the common ratio

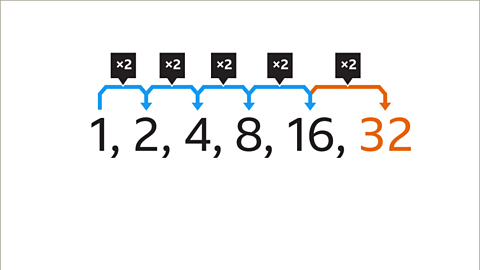
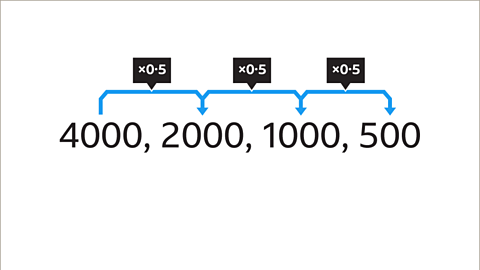
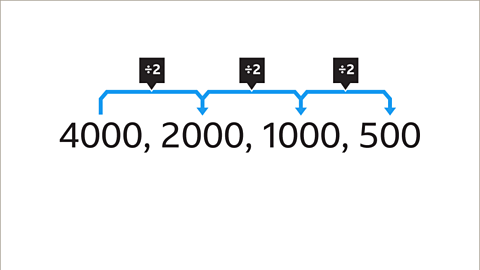
  • The common ratio is the number you multiply or divide by at each stage of the sequence. It is found by dividing two consecutive pairs of terms.

  • It does not matter which pair of terms is chosen, as long as they are next to each other in the sequence.

Examples

Image gallerySkip image gallery
  1. Example one. A sequence with the terms one hundred, two hundred, four hundred, eight hundred.
    Image caption,

    What is the common ratio of this geometric sequence of numbers?

1 of 8

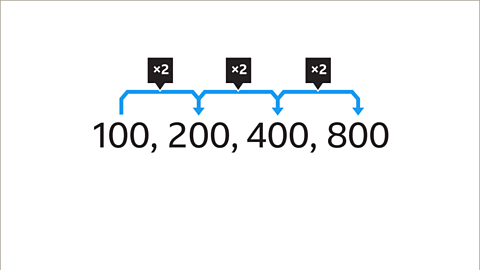
Previous imageNext imageSlide 1 of 8, Example one. A sequence with the terms one hundred, two hundred, four hundred, eight hundred. , What is the common ratio of this geometric sequence of numbers?End of image gallery

Question

What is the common ratio of this geometric sequence?

A sequence with the terms one, ten, one hundred, one thousand.

Show answer

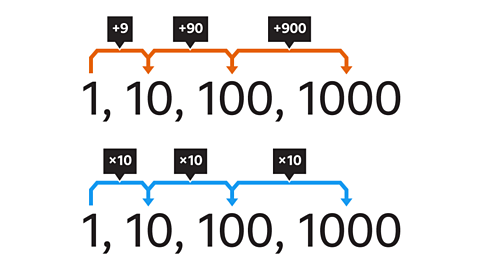
The same sequence as the previous. Written above: between each pair of terms is the amount the sequence is increasing by. Plus nine, plus ninety, plus nine hundred, with curved arrows going from left to right coloured orange. The same sequence repeated. Written above: between each pair of terms is the common ratio. Multiply by ten, multiply by ten, multiply by ten, with curved arrows going from left to right coloured blue.

  • The common ratio is the number you multiply or divide by at each stage of the sequence.

  • The differences between the terms are not the same each time, this is found by subtracting consecutive terms.

  • The differences are 9, 90 & 900. This shows that it is not an arithmetic linear sequence.

  • The common ratio is found by dividing two consecutive pairs of terms.10 ÷ 1 = 10, 100 ÷ 10 = 10 and 1000 ÷ 100 = 10

  • The next term in the sequence is calculated by multiplying the last term by 10, so the common ratio is 10

Back to top

Practise geometric sequences

Quiz

Practise recognising and finding terms in geometric sequences with this quiz. You may need a pen and paper to help you with your answers.

Back to top

Real-life maths

An image of a microbiologist inspecting a petri dish.
Image caption, Scientists like microbiologists use geometric sequences to monitor the growth of bacteria.

Geometric sequences are used in everyday life when something follows a pattern. An example of this is in scientific work, when the growth of bacteria is monitored.

If provided with the optimum conditions for growth, the population of bacteria grows in a geometric sequence, because bacteria reproduce by dividing into two.

Scientists, such as microbiologists, can predict how much bacteria will develop in a petri dish after a certain number of days by finding the common ratio.

An image of a microbiologist inspecting a petri dish.
Image caption, Scientists like microbiologists use geometric sequences to monitor the growth of bacteria.
Back to top

Play Sudoku with BBC Bitesize!

Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

Play Sudoku with BBC Bitesize!Back to top

More on Patterns and sequences

Find out more by working through a topic

  • Other sequences

    • count4 of 4

  • Finding number patterns in arithmetic sequences

    • count1 of 4

  • Finding the 𝒏th term of an arithmetic sequence

    • count2 of 4

Tag » What Is The Common Ratio