When Does A Limit Exist? | Brilliant Math & Science Wiki

Home » When Do Limits Not Exist » When Does A Limit Exist? | Brilliant Math & Science Wiki

Maybe your like

A common situation where the limit of a function does not exist is when the one-sided limits exist and are not equal: the function "jumps" at the point.

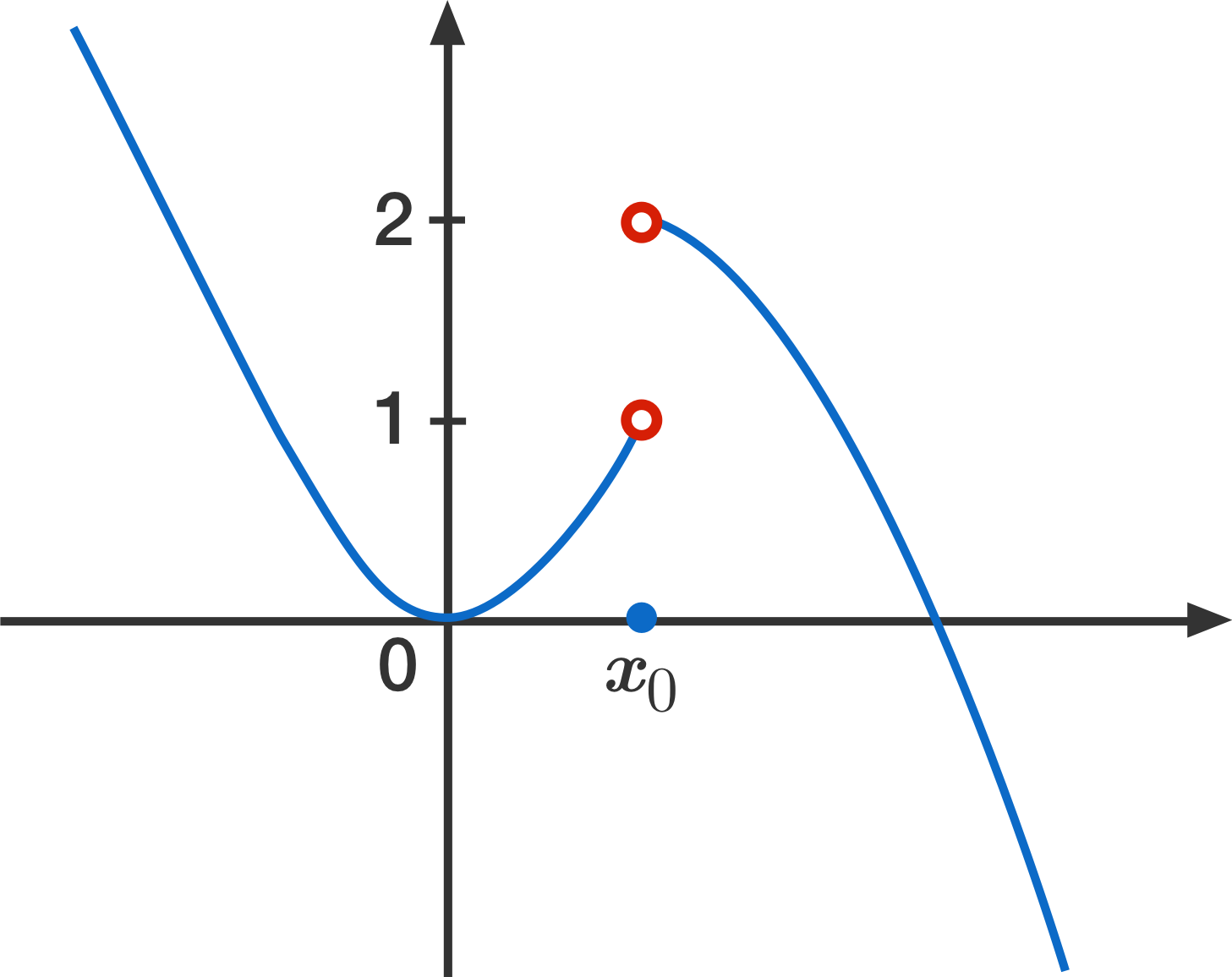The limit of \(f\) at \(x_0\) does not exist. The limit of \(f\) at \(x_0\) does not exist. [1]

For the function \(f\) in the picture, the one-sided limits \( \lim\limits_{x\to x_0^-} f(x)\) and \( \lim\limits_{x\to x_0^+} f(x)\) both exist, but they are not the same, which is a requirement for the (two-sided) limit to exist. This is usually written

\[\lim_{x \to x_0} f(x) = \text{DNE},\]

where "DNE" stands for "does not exist."

There are ane or more correct answers.

\[ \lim_{x\to5^+} f(x) = 1 \] \[ \lim_{x\to5^-} f(x) = 0 \] \[ \lim_{x\to5^+} f(x) = 4 \] \[ \lim_{x\to5^-} f(x) = 1 \] \[ \lim_{x\to5^+} f(x) = 0 \] \[ \lim_{x\to5} f(x) \text{ does not exist} \] \[ \lim_{x\to5} f(x) \text{ exists} \] Reveal the answer

Let \(\displaystyle f(x) = \frac{x^2-9x+20}{x-\lfloor x \rfloor},\) then which of the following are correct?

Notation: \( \lfloor \cdot \rfloor \) denotes the floor function.

The correct answer is: \[ \lim_{x\to5^+} f(x) = 1 \], \[ \lim_{x\to5^-} f(x) = 0 \], and \[ \lim_{x\to5} f(x) \text{ does not exist} \]

Tag » When Do Limits Not Exist