10 điểm Bảng Nguyên Hàm đầy đủ

Chuyển đến nội dung

Công thức nguyên hàm là phần quan trọng trong giải tích 12, hệ thống công thức đó được lập thành bảng nguyên hàm. Trong đề thi gần đây, các câu đòi hỏi học sinh phải nhớ công thức trong bảng là khá nhiều.

Lý thuyết

Định nghĩa: \(\int {f(x)dx = F(x) + C \Leftrightarrow F'(x) = f(x)} \)

Tính chất:

• \(\int {f'(x)dx = f(x) + C} \)
• \(\int {kf(x)dx = k\int {f(x)dx} } \) với \(\forall k \ne 0\).
• \(\int {\left[ {f(x) \pm g(x)} \right]dx = } \int {f(x)dx}  \pm \int {g(x)dx} \)

Bảng nguyên hàm đầy đủ

Phân dạng

Dạng 1: Tìm nguyên hàm của hàm số.

Phương pháp:

• Bước 1: Biến đổi hàm số \(f\left( x \right)\) về các hàm số sơ cấp có nguyên hàm đã biết.
•  Bước 2: Sử dụng định nghĩa, tính chất, bảng nguyên hàm,…để tìm nguyên hàm các hàm số.

Dạng 2: Tìm hàm số cho biết đạo hàm và giá trị của hàm số tại một điểm.

• Bước 1: Tìm nguyên hàm của hàm số đã cho, sử dụng định nghĩa, tính chất, bảng nguyên hàm,…
• Bước 2: Thay giá trị đề bài cho vào và tìm hằng số \(C\) suy ra hàm số cần tìm.

Dạng 3. Phương pháp nguyên hàm biến đổi

1. Kiến thức cần nhớ

– Vi phân:

\(\begin{array}{l}t = u\left( x \right) \Rightarrow dt = u’\left( x \right)dx\\u\left( t \right) = v\left( x \right) \Rightarrow u’\left( t \right)dt = v’\left( x \right)dx\end{array}\)

– Công thức đổi biến:

\(\int {f\left[ {u\left( x \right)} \right]u’\left( x \right)dx}  = \int {f\left( t \right)dt} \) \( = F\left( t \right) + C = F\left( {t\left( x \right)} \right) + C\)

2. Một số dạng toán thường gặp

TH 1: Tính nguyên hàm bằng phương pháp đổi biến \(t = u\left( x \right)\).

• Bước 1: Đặt \(t = u\left( x \right)\), trong đó \(u\left( x \right)\) là hàm được chọn thích hợp.
• Bước 2: Tính vi phân \(dt = u’\left( x \right)dx\).
• Bước 3: Biến đổi \(f\left( x \right)dx\) thành \(g\left( t \right)dt\).
• Bước 4: Tính nguyên hàm: \(\int {f\left( x \right)dx}  = \int {g\left( t \right)dt} \) \( = G\left( t \right) + C = G\left( {u\left( x \right)} \right) + C\).

TH 2: Dựa bảng nguyên hàm hãy tính nguyên hàm bằng phương pháp đổi biến \(x = u\left( t \right)\).

• Bước 1: Đặt \(x = u\left( t \right)\), trong đó \(u\left( t \right)\) là hàm số ta chọn thích hợp.
•  Bước 2: Lấy vi phân 2 vế \(dx = u’\left( t \right)dt\).
• – Bước 3: Biến đổi \(f\left( x \right)dx = f\left( {u\left( t \right)} \right).u’\left( t \right)dt = g\left( t \right)dt\).
•  Bước 4: Tính nguyên hàm theo công thức \(\int {f\left( x \right)dx}  = \int {g\left( t \right)dt}  = G\left( t \right) + C\)

Dạng 4. Phương pháp nguyên hàm từng phần

1. Kiến thức cần nhớ

– Công thức nguyên hàm từng phần: \(\int {udv}  = uv – \int {vdu} \)

2. Bài toán

Tính nguyên hàm \(\int {f\left( x \right)dx} = \int {g\left( x \right).h\left( x \right)dx} \)

Phương pháp:

• Bước 1: Đặt \(\left\{ \begin{array}{l}u = g\left( x \right)\\dv = h\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = g’\left( x \right)dx\\v = \int {h\left( x \right)dx} \end{array} \right.\) (\(v\left( x \right)\) là một nguyên hàm của \(h\left( x \right)\))
• Bước 2: Tính nguyên hàm theo công thức \(\int {f\left( x \right)dx}  = uv – \int {vdu} \)

Dạng 5. Phương pháp nguyên hàm hữu tỉ

Bài toán tổng quát: Tính nguyên hàm 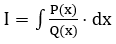 với P(x) và Q(x) là các đa thức không căn.

Phương pháp giải:

Nếu bậc của tử số P(x)≥ bậc của mẫu số Q(x) 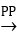 Chia đa thức.

Nếu bậc của tử số P(x) < bậc của mẫu số Q(x) 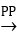 Xem xét mẫu số và khi đó:

+ Nếu mẫu số phân tích được thành tích số, ta sẽ sử dụng đồng nhất thức để đưa về dạng tổng của các phân số.

Một số trường hợp đồng nhất thức thường gặp:

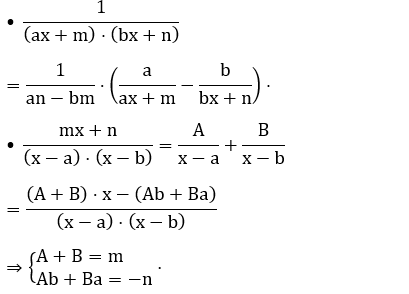
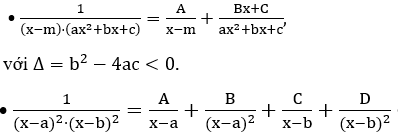
+ Nếu mẫu số không phân tích được thành tích số (biến đổi và đưa về dạng lượng giác).

Dạng 6. Tìm nguyên hàm thỏa mãn điều kiện cho trước

Bước 1: Tìm nguyên hàm dựa vào những phương pháp đã biết:

•  Sử dụng bảng nguyên hàm.
• Đổi biến số
• Nguyên hàm từng phần
• …

Bước 2: Dựa vào yêu cầu của bài toán tìm ra hằng số C tương ứng.

Bước 3: Kết luận một nguyên hàm vừa tìm được.

Hy vọng với hướng dẫn chi tiết trên sẽ giúp em học tốt nguyên hàm một cách hiệu quả.

Bài viết mới

• Những điểm tới hạn trong dao động điều hòa
• Công thức tìm khoảng thời gian ngắn nhất
• Lực kéo về trong dao động điều hòa
• Thời gian nén trong một chu kì con lắc lò xo
• Sai số phép đo các đại lượng vật lí trong đề thi 2017
• Cực trị quãng đường trong dao động điều hòa
• Chuyên đề năng lượng dao động con lắc lò xo
• Hệ thức độc lập trong dao động điều hòa
• Con lắc lò xo treo thẳng đứng hay và khó
• Những kiến thức căn bản về dao động tắt dần

Chuyên mục

Chuyên mục Chọn chuyên mục Con Lắc Đơn Con Lắc Lò Xo Dao Động Điều Hòa Dao động Tắt Dần GIẢI TOÁN BẰNG MÁY TÍNH CASIO Giao thoa sóng cơ Hàm số lũy thừa hàm số mũ và hàm số logarit Hóa học Hỏi Đáp Khối đa diện Mặt nón mặt trụ và mặt cầu nguyên hàm Nguyên hàm Tích phân và ứng dụng Phương pháp tọa độ trong không gian SÁCH TOÁN ÔN THI THPT Số phức Sóng âm Sóng cơ và sự truyền sóng cơ Sóng dừng Tích phân Tin tuyển sinh Toán toán 12 toán học Tổng Hợp Dao Động Trọn bộ dao động cơ Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

• Toán 12
• Tăng Giáp
• Sách ôn thi
• Con lắc lò xo
• lượng giác
• đạo hàm
• Toán học