2 Cách Chia đa Thức Bằng Hoocne, Hoocne Bằng Máy Tính

Chia đa thức cho đa thức?

Chẳng hạn như việc tìm thương và số dư trong phép chia, phân tích đa thức thành nhân tử, tìm nghiệm của đa thức, tìm nghiệm của phương trình, kiểm tra xem nghiệm tìm được là nghiệm đơn hay nghiệm kép, …

Trong trường hợp đặc biệt, khi đa thức chia có dạng $x-c$ thì chúng ta có thể thực hiện chia một cách nhanh chóng và dễ dàng bằng cách dựa vào sơ đồ Hoocne.

Vậy sơ đồ Hoocne là sơ đồ như thế nào? Cách chia sơ đồ Hoocne ra làm sao? Mời các bạn tham khảo bài hướng dẫn dưới đây…

Mục Lục Nội Dung

• Sơ đồ Hoocne là gì?
• Cách 1. Sử dụng kiến thức Toán học
• Cách 2. Sử dụng máy tính CASIO
• Lời kết

Sơ đồ Hoocne là gì?

Sơ đồ hoocne bản chất là một thuật toán được biểu diễn dưới dạng sơ đồ, cho phép chúng ta tìm nhanh thương và dư trong phép chia một đa thức f(x) bất kỳ cho đa thức $x-c$, với $c$ là một số thực bất kỳ.

Cách 1. Sử dụng kiến thức Toán học

Cho đa thức $f(x)=a_0x^n+a_1x^{n-1}+\cdots+a_n$

Khi chia đa thức f(x) cho đa thức $x-c$ thì chúng ta sẽ thu được một đa thức thương $q(x)=b_0x^{n-1}+b_1x^{n-2}+\cdots+b_{n-1}$ và một số dư $r$

$$a_0x^n+a_1x^{n-1}+\cdots+a_n=(x-c)(b_0x^{n-1}+b_1x^{n-2}+\cdots+b_{n-1})+r$$

Sử dụng phương pháp hệ số bất định chúng ta sẽ thu được dãy đẳng thức truy hồi …

$a_0=b_0 \Rightarrow b_0=a_0$

$a_1=b_1-cb_0 \Rightarrow b_1=cb_0+a_1$

$a_2=b_2-cb_1 \Rightarrow b_2=cb_1+a_2$

$\cdots$

$a_n=b_n-cb_{n-1} \Rightarrow b_n=cb_{n-1}+a_n$

Để dễ nhớ cũng như dễ thực hiện thì chúng ta sẽ biểu diễn dãy thức thức truy hồi trên dưới dạng sơ đồ hoocne.

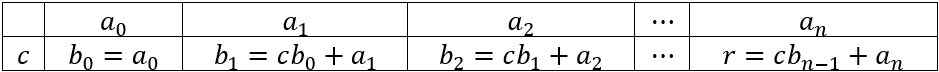
Mẹo nhớ:

• Phần tử đầu tiên ở dòng dưới bằng phần tử đầu tiên ở dòng trên.
• Mỗi phần tử ở dòng dưới bằng tích của $c$ với phần tử dừng ngay trước nó, cộng với phần tử tương ứng ở dòng trên.

Chú ý:

• Đa thức q(x) có bậc $n-1$
• Nếu $r=0$ thì $c$ chính là nghiệm của đa thức $f(x)$

Ví dụ 1. Tìm thương và dư trong phép chia đa thức $f(x)=2x^4-x^3-x^2+3x-2$ cho đa thức $g(x)=x-2$

Gợi ý:

Lần lượt viết các hệ số của f(x) vào dòng đầu tiên.

g(x) của chúng ta là $x-2$ suy ra $c$ của chúng ta là $2$

Lời giải:

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

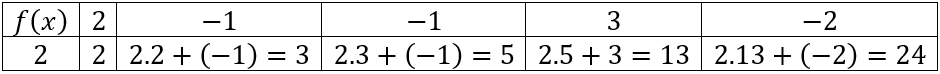
Vậy đa thức thương là $2x^3+3x^2+5x+13$ và dư là $24$

Ví dụ 2. Tìm thương và dư trong phép chia đa thức $f(x)=x^4-x^2+2x-3$ cho đa thức $g(x)=x+1$

Gợi ý:

• Lần lượt viết các hệ số của f(x) vào dòng đầu tiên, hệ số của $x^3$ là $0$
• g(x) của chúng ta là $x+1$ suy ra $c$ của chúng ta $-1$

Lời giải:

Vậy đa thức thương là $x^3-x^2+2$ và dư là $-5$

Cách 2. Sử dụng máy tính CASIO

Thuật giải này sẽ rất hữu ích khi đa thức của chúng ta có bậc lớn hoặc hệ số lớn hoặc số “xấu”

Giả sử mình cần tìm thương và dư trong phép chia đa thức $f(x)=x^4-x^2+2x-3$ cho đa thức $g(x)=x+1$ bằng máy tính CASIO fx-580VN X

Bước 1. Lập bảng như hình bên dưới (nếu bạn có trí nhớ tốt thì nhớ luôn trong đầu mà không cần lập bảng)

Bước 2. Nhập hệ số đầu tiên của dòng dưới => rồi nhấn phím =

Bước 3. Nhấn phím AC => rồi nhập cAns+X, c ở đây là -1

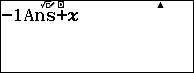
Bước 4. Nhấn CALC rồi nhập hệ số thứ hai của dòng trên, ở đây là 0 sau đó nhấn phím = chúng ta sẽ thu được hệ số thứ hai của dòng dưới.

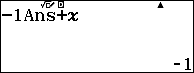
Bước 5. Thực hiện lại Bước 4 với các hệ số còn lại.

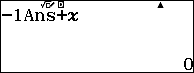
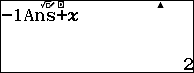
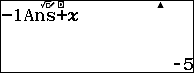
Chú ý: Bạn phải thực hiện chính xác theo tuần tự các bước trong thuật toán, không được sai sót ở bất cứ một bước nào, nếu sai phải thực hiện lại TỪ ĐẦU

Xem video thao tác chia bằng sơ đồ Hoocne

Lời kết

Khi thực hành giải toán, bất cứ khi nào bạn cần chia đa thức cho đa thức mà đa thức chia có dạng $x-c$ thì nên sử dụng sơ đồ Hoocne để thực hiện cho nhanh.

Ngoài việc giải nhanh ra thì sử dụng phương pháp này sẽ giúp bạn tránh khỏi những sai sót không đáng có. Không những thế, khi kết hợp sơ đồ Hoocne với định lý Bơdu thì chúng ta còn có thể tính nhanh giá trị của $f(c)=r$, rất hữu ích khi f(x) có bậc cao.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com Edit by Kiên Nguyễn

Bài viết đạt: 5/5 sao - (Có 2 lượt đánh giá)