20 Bài Tập Vận Dụng Đường Trung Bình Của Tam Giác, Của Hình Thang

Có thể bạn quan tâm

Lớp 12
- Ngữ văn 12
  - Soạn văn - Kết nối tri thức
  - Soạn văn - Cánh diều
  - Soạn văn - Chân trời sáng tạo
  - Tác giả tác phẩm
  - Tóm tắt, bố cục Văn - Kết nối tri thức
  - Tóm tắt, bố cục Văn - Cánh diều
  - Tóm tắt, bố cục Văn - Chân trời sáng tạo
  - SBT Văn - Kết nối tri thức
  - >> Xem thêm
- Toán học 12
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Cánh diều
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cùng khám phá
  - SBT Toán - Kết nối tri thức
  - SBT Toán - Cánh diều
  - SBT Toán - Chân trời sáng tạo
  - Chuyên đề học tập Toán - Kết nối tri thức
  - >> Xem thêm
- Tiếng Anh 12
  - Tiếng Anh - Global Success
  - Tiếng Anh - Friends Global
  - Tiếng Anh - iLearn Smart World
  - Tiếng Anh - Bright
  - Tiếng Anh - English Discovery
  - SBT Global Success
  - SBT Friends Global
  - SBT iLearn Smart World
  - >> Xem thêm
- Vật lí 12
  - SGK Vật Lí - Kết nối tri thức
  - SGK Vật Lí - Cánh diều
  - SGK Vật Lí - Chân trời sáng tạo
  - SBT Vật lí - Kết nối tri thức
  - SBT Vật lí - Cánh diều
  - SBT Vật lí - Chân trời sáng tạo
  - Chuyên đề học tập Lí - Kết nối tri thức
  - Chuyên đề học tập Lí - Cánh diều
  - >> Xem thêm
- Hóa học 12
  - SGK Hóa - Kết nối tri thức
  - SGK Hóa - Cánh diều
  - SGK Hóa - Chân trời sáng tạo
  - SBT Hóa - Kết nối tri thức
  - SBT Hóa - Cánh diều
  - SBT Hóa - Chân trời sáng tạo
  - Chuyên đề học tập Hóa - Kết nối tri thức
  - Chuyên đề học tập Hóa - Cánh diều
  - >> Xem thêm
- Sinh học 12
  - SGK Sinh - Kết nối tri thức
  - SGK Sinh - Cánh diều
  - SGK Sinh - Chân trời sáng tạo
  - Trắc nghiệm Sinh - Kết nối tri thức
  - Trắc nghiệm Sinh - Cánh diều
  - Trắc nghiệm Sinh - Chân trời sáng tạo
  - Chuyên đề học tập Sinh - Kết nối tri thức
  - Chuyên đề học tập Sinh - Cánh diều
  - >> Xem thêm
- Lịch sử 12
  - SGK Lịch sử - Kết nối tri thức
  - SGK Lịch sử - Chân trời sáng tạo
  - SGK Lịch sử - Cánh diều
  - SBT Lịch sử - Cánh diều
  - Đề thi, đề kiểm tra Lịch sử - Kết nối tri thức
  - Đề thi, đề kiểm tra Lịch sử - Chân trời sáng tạo
  - Đề thi, đề kiểm tra Lịch sử - Cánh diều
  - Chuyên đề học tập Lịch sử - Kết nối tri thức
  - >> Xem thêm
- Địa lí 12
  - SGK Địa lí - Kết nối tri thức
  - SGK Địa lí - Chân trời sáng tạo
  - SGK Địa lí - Cánh diều
  - SBT Địa lí - Cánh diều
  - Đề thi, đề kiểm tra Địa lí - Kết nối tri thức
  - Đề thi, đề kiểm tra Địa lí - Chân trời sáng tạo
  - Đề thi, đề kiểm tra Địa lí - Cánh diều
  - SBT Địa lí - Chân trời sáng tạo
  - >> Xem thêm
- GD kinh tế và pháp luật 12
  - SGK Giáo dục kinh tế và pháp luật - Kết nối tri thức
  - SGK Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
  - SGK Giáo dục kinh tế và pháp luật - Cánh diều
  - SBT Giáo dục kinh tế và pháp luật - Cánh diều
  - SBT Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
  - Chuyên đề học tập Giáo dục kinh tế pháp luật - Kết nối tri thức
  - Chuyên đề học tập Giáo dục kinh tế pháp luật - Cánh diều
  - Chuyên đề học tập Giáo dục kinh tế pháp luật - Chân trời sáng tạo
- Công nghệ 12
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Cánh diều
  - Chuyên đề học tập Công nghệ - Kết nối tri thức
  - Chuyên đề học tập Công nghệ - Cánh diều
- Tin học 12
  - SGK Tin học - Cánh diều
  - SGK Tin học - Chân trời sáng tạo
  - SGK Tin học - Kết nối tri thức
  - SBT Tin học - Kết nối tri thức
  - SBT Tin học - Cánh diều
  - SBT Tin học - Chân trời sáng tạo
  - Chuyên đề học tập Tin - Kết nối tri thức
  - Chuyên đề học tập Tin - Chân trời sáng tạo
  - >> Xem thêm
- HĐ trải nghiệm, hướng nghiệp 12
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh diều
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 1
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 2
- GD Quốc phòng và An ninh 12
  - SGK Giáo dục quốc phòng và an ninh - Kết nối tri thức
  - SGK Giáo dục quốc phòng và an ninh - Cánh diều
- Giáo dục thể chất 12
  - SGK Giáo dục thể chất - Kết nối tri thức
  - SGK Giáo dục thể chất - Cánh diều
- Giáo dục địa phương 12
  - Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 12
  - Tổng hợp đề thi, đề kiểm tra
Lớp 11
- Ngữ văn 11
  - Soạn văn - Kết nối tri thức - chi tiết
  - Soạn văn - Kết nối tri thức - siêu ngắn
  - Soạn văn - Cánh Diều - chi tiết
  - Soạn văn - Cánh Diều - siêu ngắn
  - Soạn văn - Chân trời sáng tạo - chi tiết
  - Soạn văn - Chân trời sáng tạo - siêu ngắn
  - Tác giả tác phẩm
  - Tóm tắt, bố cục Văn - Kết nối tri thức
  - >> Xem thêm
- Toán học 11
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Cánh diều
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cùng khám phá
  - Chuyên đề học tập Toán - Kết nối tri thức
  - Chuyên đề học tập Toán - Cánh diều
  - Chuyên đề học tập Toán - Chân trời sáng tạo
  - SBT Toán - Kết nối tri thức
  - >> Xem thêm
- Tiếng Anh 11
  - Tiếng Anh - Global Success
  - Tiếng Anh - Friends Global
  - Tiếng Anh - iLearn Smart Wolrd
  - Tiếng Anh - Bright
  - Tiếng Anh - English Discovery
  - SBT Global Success
  - SBT Friends Global
  - SBT iLearn Smart World
  - >> Xem thêm
- Vật lí 11
  - SGK Vật Lí - Kết nối tri thức
  - SGK Vật Lí - Cánh diều
  - SGK Vật Lí - Chân trời sáng tạo
  - Chuyên đề học tập Lí - Kết nối tri thức
  - Chuyên đề học tập Lí - Cánh diều
  - Chuyên đề học tập Lí - Chân trời sáng tạo
  - SBT Vật lí - Kết nối tri thức
  - SBT Vật lí - Cánh diều
  - >> Xem thêm
- Hóa học 11
  - SGK Hóa học - Kết nối tri thức
  - SGK Hóa học - Cánh diều
  - SGK Hóa học - Chân trời sáng tạo
  - Chuyên đề học tập Hóa - Kết nối tri thức
  - Chuyên đề học tập Hóa - Cánh diều
  - Chuyên đề học tập Hóa - Chân trời sáng tạo
  - SBT Hóa - Kết nối tri thức
  - SBT Hóa - Cánh diều
  - >> Xem thêm
- Sinh học 11
  - SGK Sinh - Kết nối tri thức
  - SGK Sinh - Cánh diều
  - SGK Sinh - Chân trời sáng tạo
  - Chuyên đề học tập Sinh - Kết nối tri thức
  - Chuyên đề học tập Sinh - Cánh diều
  - Chuyên đề học tập Sinh - Chân trời sáng tạo
  - SBT Sinh - Kết nối tri thức
  - SBT Sinh - Cánh diều
  - >> Xem thêm
- HĐ trải nghiệm, hướng nghiệp 11
  - SBT Hoạt động trải nghiệm - Kết nối tri thức
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh diều
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 1
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 2
  - SBT Hoạt động trải nghiệm - Cánh diều
  - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
  - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
- Lịch sử 11
  - SGK Lịch sử - Kết nối tri thức
  - SGK Lịch sử - Chân trời sáng tạo
  - SGK Lịch sử - Cánh diều
  - SBT Lịch sử - Kết nối tri thức
  - SBT Lịch sử - Chân trời sáng tạo
  - SBT Lịch sử - Cánh diều
  - Đề thi, đề kiểm tra Lịch sử - Kết nối tri thức
  - Đề thi, đề kiểm tra Lịch sử - Chân trời sáng tạo
  - >> Xem thêm
- Địa lí 11
  - SGK Địa lí - Kết nối tri thức
  - SGK Địa lí - Chân trời sáng tạo
  - SGK Địa lí - Cánh diều
  - SBT Địa lí - Kết nối tri thức
  - SBT Địa lí - Chân trời sáng tạo
  - SBT Địa lí - Cánh diều
  - Đề thi, đề kiểm tra Địa lí - Kết nối tri thức
  - Đề thi, đề kiểm tra Địa lí - Chân trời sáng tạo
  - >> Xem thêm
- GD kinh tế và pháp luật 11
  - SGK Giáo dục kinh tế và pháp luật - Kết nối tri thức
  - SGK Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
  - SGK Giáo dục kinh tế và pháp luật - Cánh diều
  - SBT Giáo dục kinh tế và pháp luật - Kết nối tri thức
  - SBT Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
  - SBT Giáo dục kinh tế và pháp luật - Cánh diều
  - Chuyên đề học tập Giáo dục kinh tế pháp luật - Kết nối tri thức
  - Chuyên đề học tập Giáo dục kinh tế pháp luật - Chân trời sáng tạo
  - >> Xem thêm
- Công nghệ 11
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Cánh diều
- Tin học 11
  - SGK Tin học - Kết nối tri thức
  - SGK Tin học - Cánh diều
  - SBT Tin học - Kết nối tri thức
  - SBT Tin học - Cánh diều
  - Chuyên đề học tập Tin - Kết nối tri thức
  - Chuyên đề học tập Tin - Cánh diều
- Giáo dục thể chất 11
  - SGK Giáo dục thể chất - Kết nối tri thức
  - SGK Giáo dục thể chất - Cánh diều
- GD Quốc phòng và An ninh 11
  - SGK Giáo dục quốc phòng và an ninh - Kết nối tri thức
  - SGK Giáo dục quốc phòng và an ninh - Cánh diều
- Giáo dục địa phương 11
  - Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 11
  - Tổng hợp đề thi, đề kiểm tra
Lớp 10
- Ngữ văn 10
  - Soạn văn - Kết nối tri thức - siêu ngắn
  - Soạn văn - Kết nối tri thức - chi tiết
  - Soạn văn - Chân trời sáng tạo - siêu ngắn
  - Soạn văn - Chân trời sáng tạo - chi tiết
  - Soạn văn - Cánh Diều - siêu ngắn
  - Soạn văn - Cánh Diều - chi tiết
  - Tác giả tác phẩm
  - Tóm tắt, bố cục Văn - Kết nối tri thức
  - >> Xem thêm
- Toán học 10
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh diều
  - SBT Toán - Kết nối tri thức
  - SBT Toán - Chân trời sáng tạo
  - SBT Toán - Cánh diều
  - Chuyên đề học tập Toán - Kết nối tri thức
  - Chuyên đề học tập Toán - Chân trời sáng tạo
  - >> Xem thêm
- Tiếng Anh 10
  - Tiếng Anh - Global Success
  - Tiếng Anh - Friends Global
  - Tiếng Anh - iLearn Smart World
  - Tiếng Anh - English Discovery
  - Tiếng Anh - Bright
  - Tiếng Anh - Explore New Worlds
  - SBT Global Success
  - SBT Friends Global
  - >> Xem thêm
- Vật lí 10
  - SGK Vật Lí - Kết nối tri thức
  - SGK Vật Lí - Chân trời sáng tạo
  - SGK Vật Lí - Cánh diều
  - SBT Vật lí - Kết nối tri thức
  - SBT Vật lí - Chân trời sáng tạo
  - SBT Vật lí - Cánh diều
  - Trắc nghiệm Lí - Kết nối tri thức
  - Bài tập trắc nghiệm Lí - Kết nối tri thức
  - >> Xem thêm
- Hóa học 10
  - SGK Hóa - Kết nối tri thức
  - SGK Hóa - Chân trời sáng tạo
  - SGK Hóa - Cánh diều
  - SBT Hóa - Kết nối tri thức
  - SBT Hóa - Chân trời sáng tạo
  - SBT Hóa 10 - Cánh diều
  - Chuyên đề học tập Hóa - Kết nối tri thức
  - Chuyên đề học tập Hóa 10 – Chân trời sáng tạo
  - >> Xem thêm
- Sinh học 10
  - SGK Sinh - Kết nối tri thức
  - SGK Sinh - Chân trời sáng tạo
  - SGK Sinh - Cánh diều
  - SBT Sinh - Kết nối tri thức
  - SBT Sinh - Chân trời sáng tạo
  - SBT Sinh - Cánh diều
  - Chuyên đề học tập Sinh - Kết nối tri thức
  - Chuyên đề học tập Sinh - Chân trời sáng tạo
  - >> Xem thêm
- Lịch sử 10
  - SGK Lịch sử - Kết nối tri thức
  - SGK Lịch sử - Chân trời sáng tạo
  - SGK Lịch sử - Cánh Diều
  - SBT Lịch sử - Kết nối tri thức
  - SBT Lịch sử - Chân trời sáng tạo
  - SBT Lịch sử - Cánh Diều
  - Chuyên đề học tập Lịch sử - Kết nối tri thức
  - Trắc nghiệm Sử - kết nối tri thức
  - >> Xem thêm
- Địa lí 10
  - SGK Địa lí - Kết nối tri thức
  - SGK Địa lí - Cánh Diều
  - SGK Địa lí - Chân trời sáng tạo
  - SBT Địa lí - Kết nối tri thức
  - SBT Địa lí - Chân trời sáng tạo
  - Trắc nghiệm Địa lí - Kết nối tri thức
  - Trắc nghiệm Địa lí - Chân trời sáng tạo
  - Trắc nghiệm Địa lí - Cánh Diều
  - >> Xem thêm
- Tin học 10
  - SGK Tin học - Kết nối tri thức
  - SGK Tin học - Cánh Diều
  - SBT Tin học - Kết nối tri thức
  - SBT Tin học 10 - Cánh diều
- Công nghệ 10
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Cánh diều
  - Chuyên đề học tập Công nghệ - Kết nối tri thức
  - Chuyên đề học tập Công nghệ - Cánh diều
- GD kinh tế và pháp luật 10
  - SGK Giáo dục kinh tế và pháp luật - KNTT
  - SGK Giáo dục kinh tế và pháp luật - CTST
  - SGK Giáo dục kinh tế và pháp luật - Cánh diều
  - SBT Giáo dục kinh tế và pháp luật - Kết nối tri thức
  - SBT Giáo dục kinh tế và pháp luật - Chân trời sáng tạo
  - SBT Giáo dục kinh tế và pháp luật - Cánh diều
  - Chuyên đề học tập Giáo dục kinh tế pháp luật - Kết nối tri thức
  - Chuyên đề học tập Giáo dục kinh tế pháp luật - Chân trời sáng tạo
  - >> Xem thêm
- HĐ trải nghiệm, hướng nghiệp 10
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh Diều
  - SBT Hoạt động trải nghiệm - Kết nối tri thức
  - SBT Hoạt động trải nghiệm - Cánh diều
  - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
  - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
- Giáo dục thể chất 10
  - SGK Giáo dục thể chất - Kết nối tri thức
  - SGK Giáo dục thể chất - Cánh diều
- GD Quốc phòng và An ninh 10
  - SGK Giáo dục quốc phòng và an ninh - Kết nối tri thức
  - SGK Giáo dục quốc phòng và an ninh - Cánh diều
- Giáo dục địa phương 10
  - Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 10
  - Tổng hợp đề thi, đề kiểm tra
Lớp 9
- Toán học 9
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh diều
  - SGK Toán - Cùng khám phá
  - SBT Toán - Kết nối tri thức
  - SBT Toán - Chân trời sáng tạo
  - SBT Toán - Cánh diều
  - Vở thực hành Toán
  - >> Xem thêm
- Ngữ văn 9
  - Soạn văn - Kết nối tri thức
  - Soạn văn - Chân trời sáng tạo
  - Soạn văn - Cánh diều
  - Tác giả - Tác phẩm văn
  - Tóm tắt, bố cục Văn - Kết nối tri thức
  - Tóm tắt, bố cục Văn - Chân trời sáng tạo
  - Tóm tắt, bố cục Văn - Cánh diều
  - SBT Văn - Kết nối tri thức
  - >> Xem thêm
- Tiếng Anh 9
  - Tiếng Anh - Global Success
  - Tiếng Anh - Friends Plus
  - Tiếng Anh - iLearn Smart World
  - Tiếng Anh - Right on!
  - Tiếng Anh - English Discovery
  - SBT Global Success
  - SBT Friends Plus
  - SBT iLearn Smart World
  - >> Xem thêm
- Khoa học tự nhiên 9
  - SGK Khoa học tự nhiên - Kết nối tri thức
  - SGK Khoa học tự nhiên - Cánh diều
  - SGK Khoa học tự nhiên 9 Chân trời sáng tạo
  - SBT KHTN - Kết nối tri thức
  - SBT KHTN - Cánh diều
  - SBT KHTN - Chân trời sáng tạo
  - Trắc nghiệm KHTN - Kết nối tri thức
  - Trắc nghiệm KHTN - Cánh diều
  - >> Xem thêm
- Lịch sử và Địa lí 9
  - SGK Lịch sử và Địa lí - Kết nối tri thức
  - SGK Lịch sử và Địa lí - Cánh diều
  - SGK Lịch sử và Địa lí - Chân trời sáng tạo
  - SBT Lịch sử - Cánh diều
  - SBT Địa lí - Kết nối tri thức
  - SBT Địa lí - Chân trời sáng tạo
  - SBT Đia lí - Cánh diều
  - Đề thi, kiểm tra Lịch Sử và Địa lí - Kết nối tri thức
  - >> Xem thêm
- GDCD 9
  - Giáo dục công dân - Kết nối tri thức
  - Giáo dục công dân - Chân trời sáng tạo
  - Giáo dục công dân - Cánh diều
  - SBT GDCD - Chân trời sáng tạo
  - SBT GDCD - Cánh diều
- Tin học 9
  - SGK Tin học - Kết nối tri thức
  - SGK Tin học - Cánh diều
  - SGK Tin học - Chân trời sáng tạo
  - SBT Tin học - Kết nối tri thức
  - SBT Tin học - Chân trời sáng tạo
  - SBT Tin học - Cánh diều
- Công nghệ 9
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Chân trời sáng tạo
  - SGK Công nghệ - Cánh diều
  - SBT Công nghệ - Cánh diều
- HĐ trải nghiệm, hướng nghiệp 9
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh diều
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 1
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 2
- Giáo dục địa phương 9
  - Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 9
  - Tổng hợp đề thi, đề kiểm tra
  - Tổng hợp đề thi vào 10
Lớp 8
- Ngữ văn 8
  - Soạn văn chi tiết - KNTT
  - Soạn văn siêu ngắn - KNTT
  - Soạn văn chi tiết - CTST
  - Soạn văn siêu ngắn - CTST
  - Soạn văn chi tiết - Cánh diều
  - Soạn văn siêu ngắn - Cánh diều
  - Tác giả - Tác phẩm văn
  - Tóm tắt, bố cục Văn - Kết nối tri thức
  - >> Xem thêm
- Toán học 8
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh diều
  - SGK Toán - Cùng khám phá
  - SBT Toán - Kết nối tri thức
  - SBT Toán - Chân trời sáng tạo
  - SBT Toán - Cánh diều
  - Vở thực hành Toán
  - >> Xem thêm
- Tiếng Anh 8
  - Tiếng Anh - Global Success
  - Tiếng Anh - Friends Plus
  - Tiếng Anh - iLearn Smart World
  - Tiếng Anh - Right on!
  - Tiếng Anh - English Discovery
  - SBT Global Success
  - SBT Friends Plus
  - SBT iLearn Smart World
  - >> Xem thêm
- Khoa học tự nhiên 8
  - SGK Khoa học tự nhiên - Kết nối tri thức
  - SGK Khoa học tự nhiên - Chân trời sáng tạo
  - SGK Khoa học tự nhiên - Cánh diều
  - SBT KHTN - Kết nối tri thức
  - SBT KHTN - Cánh diều
  - Vở thực hành Khoa học tự nhiên
  - Đề thi, đề kiểm tra KHTN - Kết nối tri thức
  - Đề thi, đề kiểm tra KHTN - Cánh diều
  - >> Xem thêm
- Lịch sử và Địa lí 8
  - SGK Lịch sử và Địa lí - Kết nối tri thức
  - SGK Lịch sử và Địa lí - Cánh diều
  - SGK Lịch sử và Địa lí - Chân trời sáng tạo
  - SBT Lịch sử - Kết nối tri thức
  - SBT Địa lí - Kết nối tri thức
  - SBT Lịch sử - Chân trời sáng tạo
  - SBT Địa lí - Chân trời sáng tạo
  - SBT Lịch sử - Cánh diều
  - >> Xem thêm
- GDCD 8
  - Giáo dục công dân - Kết nối tri thức
  - Giáo dục công dân - Chân trời sáng tạo
  - Giáo dục công dân - Cánh diều
  - SBT GDCD - Kết nối tri thức
  - SBT GDCD - Chân trời sáng tạo
  - SBT GDCD - Cánh diều
- Công nghệ 8
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Chân trời sáng tạo
  - SGK Công nghệ - Cánh diều
  - SBT Công nghệ - Kết nối tri thức
  - SBT Công nghệ - Chân trời sáng tạo
  - SBT Công nghệ - Cánh diều
- Tin học 8
  - SGK Tin học - Kết nối tri thức
  - SGK Tin học - Chân trời sáng tạo
  - SGK Tin học - Cánh diều
  - SBT Tin học - Kết nối tri thức
  - SBT Tin học - Chân trời sáng tạo
  - SBT Tin học - Cánh diều
- HĐ trải nghiệm, hướng nghiệp 8
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh diều
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 1
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo Bản 2
  - SBT Hoạt động trải nghiệm - Kết nối tri thức
  - SBT Hoạt động trải nghiệm - Cánh diều
  - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
  - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
- Âm nhạc 8
  - SGK Âm nhạc - Kết nối tri thức
  - SGK Âm nhạc - Chân trời sáng tạo
  - SGK Âm nhạc - Cánh diều
- Mỹ thuật 8
  - SGK Mĩ thuật - Kết nối tri thức
  - SGK Mĩ thuật - Chân trời sáng tạo bản 1
  - SGK Mĩ thuật - Cánh diều
  - SGK Mĩ thuật - Chân trời sáng tạo bản 2
- Giáo dục thể chất 8
  - SGK Giáo dục thể chất - Kết nối tri thức
  - SGK Giáo dục thể chất - Cánh diều
  - SGK Giáo dục thể chất - Chân trời sáng tạo
- Giáo dục địa phương 8
  - Đề thi, đề kiểm tra Giáo dục địa phương
  - Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 8
  - Tổng hợp đề thi, đề kiểm tra
Lớp 7
- Ngữ văn 7
  - Soạn văn siêu ngắn - KNTT
  - Soạn văn chi tiết - KNTT
  - Soạn văn siêu ngắn - CTST
  - Soạn văn chi tiết - CTST
  - Soạn văn siêu ngắn - Cánh diều
  - Soạn văn chi tiết - Cánh diều
  - Tác giả - Tác phẩm văn
  - Tóm tắt, bố cục Văn - Kết nối tri thức
  - >> Xem thêm
- Toán học 7
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh diều
  - SBT Toán - Kết nối tri thức
  - SBT Toán - Chân trời sáng tạo
  - SBT Toán - Cánh diều
  - Trắc nghiệm Toán - Kết nối tri thức
  - Trắc nghiệm Toán- Chân trời sáng tạo
  - >> Xem thêm
- Tiếng Anh 7
  - Tiếng Anh - Global Success
  - Tiếng Anh - Friends Plus
  - Tiếng Anh - iLearn Smart World
  - Tiếng Anh - English Discovery
  - Tiếng Anh - Right on!
  - SBT Global Success
  - SBT Friends Plus
  - SBT iLearn Smart World
  - >> Xem thêm
- Khoa học tự nhiên 7
  - SGK Khoa học tự nhiên - Kết nối tri thức
  - SGK Khoa học tự nhiên - Chân trời sáng tạo
  - SGK Khoa học tự nhiên - Cánh diều
  - SBT KHTN - Kết nối tri thức
  - SBT KHTN - Chân trời sáng tạo
  - SBT KHTN - Cánh diều
  - Trắc nghiệm KHTN - Kết nối tri thức
  - Bài tập trắc nghiệm Khoa học tự nhiên - Kết nối tri thức
  - >> Xem thêm
- Lịch sử và Địa lí 7
  - SGK Lịch sử và Địa lí - Kết nối tri thức
  - SGK Lịch sử và Địa lí - Chân trời sáng tạo
  - SGK Lịch sử và Địa lí - Cánh Diều
  - SBT Lịch sử và Địa lí - Kết nối tri thức
  - SBT Lịch sử và Địa lí - Chân trời sáng tạo
  - SBT Lịch sử và Địa lí - Cánh diều
  - Trắc nghiệm Lịch sử và Địa lí - Kết nối tri thức
  - Trắc nghiệm Lịch sử và Địa lí - Chân trời sáng tạo
  - >> Xem thêm
- Tin học 7
  - SGK Tin học - Kết nối tri thức
  - SGK Tin học - Cánh Diều
  - SGK Tin học - Chân trời sáng tạo
  - SBT Tin học - Kết nối tri thức
  - SBT Tin học - Chân trời sáng tạo
  - SBT Tin học - Cánh diều
- Công nghệ 7
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Chân trời sáng tạo
  - SGK Công nghệ - Cánh diều
  - SBT Công nghệ - Kết nối tri thức
  - SBT Công nghệ - Chân trời sáng tạo
  - SBT Công nghệ - Cánh diều
- GDCD 7
  - SGK GDCD - KNTT
  - SGK GDCD - CTST
  - SGK GDCD - Cánh diều
  - Bài tập tình huống GDCD
  - SBT GDCD - Kết nối tri thức
  - SBT GDCD - Chân trời sáng tạo
  - SBT GDCD - Cánh diều
- HĐ trải nghiệm, hướng nghiệp 7
  - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Kết nối tri thức
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Cánh Diều
  - SGK Hoạt động trải nghiệm, hướng nghiệp - Chân trời sáng tạo
  - SBT Hoạt động trải nghiệm - Cánh diều
  - SBT Hoạt động trải nghiệm - Kết nối tri thức
  - SBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
- Âm nhạc 7
  - Âm nhạc - Kết nối tri thức
  - Âm nhạc - Chân trời sáng tạo
  - Âm nhạc - Cánh diều
- Giáo dục địa phương 7
  - Đề thi, đề kiểm tra Giáo dục địa phương 7
  - Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 7
  - Tổng hợp đề thi, đề kiểm tra
Lớp 6
- Ngữ văn 6
  - Soạn văn siêu ngắn - KNTT
  - Soạn văn chi tiết - KNTT
  - Soạn văn siêu ngắn - CTST
  - Soạn văn chi tiết - CTST
  - Soạn văn siêu ngắn - Cánh diều
  - Soạn văn chi tiết - Cánh diều
  - Tác giả - Tác phẩm văn
  - Tóm tắt, bố cục Văn - Kết nối tri thức
  - >> Xem thêm
- Toán học 6
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh diều
  - SBT Toán - Kết nối tri thức
  - SBT Toán - Chân trời sáng tạo
  - SBT Toán - Cánh diều
  - Trắc nghiệm Toán - Kết nối tri thức
  - Trắc nghiệm Toán - Chân trời sáng tạo
  - >> Xem thêm
- Tiếng Anh 6
  - Global Success (Pearson)
  - Tiếng Anh - Friends plus
  - Tiếng Anh - iLearn Smart World
  - Tiếng Anh - Right on
  - Tiếng Anh - English Discovery
  - Tiếng Anh - Explore English
  - SBT Global Success
  - SBT Friends Plus
  - >> Xem thêm
- Khoa học tự nhiên 6
  - SGK KHTN - Kết nối tri thức
  - SGK KHTN - Chân trời sáng tạo
  - SGK KHTN - Cánh Diều
  - SBT KHTN - Kết nối tri thức
  - SBT KHTN - Chân trời sáng tạo
  - SBT KHTN - Cánh Diều
  - Trắc nghiệm KHTN - Kết nối tri thức
  - Trắc nghiệm KHTN - Chân trời sáng tạo
  - >> Xem thêm
- Lịch sử và Địa lí 6
  - SGK Lịch sử và Địa lí - KNTT
  - SGK Lịch sử và Địa lí - CTST
  - SGK Lịch sử và Địa lí - Cánh Diều
  - SBT Lịch sử và Địa lí - KNTT
  - SBT Lịch sử và Địa lí - CTST
  - SBT Lịch sử và Địa lí - Cánh diều
  - Trắc nghiệm Lịch sử và Địa Lí - KNTT
  - Trắc nghiệm Lịch Sử và Địa Lí - CTST
  - >> Xem thêm
- GDCD 6
  - SGK GDCD - KNTT
  - SGK GDCD - CTST
  - SGK GDCD - Cánh Diều
  - SBT GDCD - Kết nối tri thức
  - SBT GDCD - Chân trời sáng tạo
  - SBT GDCD - Cánh diều
- Công nghệ 6
  - Công nghệ - Kết nối tri thức
  - Công nghệ - Cánh Diều
  - Công nghệ - Chân trời sáng tạo
  - SBT Công nghệ - Kết nối tri thức
  - SBT Công nghệ - Cánh diều
  - SBT Công nghệ - Chân trời sáng tạo
- Tin học 6
  - Tin học - Kết nối tri thức + chân trời sáng tạo
  - Tin học - Cánh Diều
  - SBT Tin học - Kết nối tri thức
  - SBT Tin học - Cánh Diều
- HĐ trải nghiệm, hướng nghiệp 6
  - SGK Trải nghiệm, hướng nghiệp - Kết nối tri thức
  - SGK Trải nghiệm, hướng nghiệp - Chân trời sáng tạo
  - SGK Trải nghiệm, hướng nghiệp - Cánh diều
  - SBT Trải nghiệm, hướng nghiệp - Kết nối tri thức
  - SBT Trải nghiệm, hướng nghiệp - Chân trời sáng tạo
  - Thực hành Trải nghiệm, hướng nghiệp - Cánh diều
- Âm nhạc 6
  - Âm nhạc - Kết nối tri thức
  - Âm nhạc - Cánh Diều
  - Âm nhạc: Chân trời sáng tạo
- Mỹ thuật 6
  - Mĩ thuật - Kết nối tri thức
  - Mĩ thuật - Chân trời sáng tạo
  - Mĩ thuật - Cánh diều
- Giáo dục địa phương 6
  - Đề thi, đề kiểm tra Giáo dục địa phương
  - Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 6
  - Tổng hợp đề thi, đề kiểm tra
Lớp 5
- Toán học 5
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh diều
  - SGK Toán - Bình Minh
  - VBT Toán - Kết nối tri thức
  - VBT Toán - Cánh diều
  - Trắc nghiệm Toán - Kết nối tri thức
  - Trắc nghiệm Toán - Chân trời sáng tạo
  - >> Xem thêm
- Tiếng việt 5
  - Tiếng Việt - Kết nối tri thức
  - Tiếng Việt - Chân trời sáng tạo
  - Tiếng Việt - Cánh diều
  - VBT Tiếng Việt - Kết nối tri thức
  - VBT Tiếng Việt - Chân trời sáng tạo
  - VBT Tiếng Việt - Cánh diều
  - Văn mẫu lớp 5
  - Đề thi, đề kiểm tra Tiếng Việt - Kết nối tri thức
  - >> Xem thêm
- Tiếng Anh 5
  - Tiếng Anh - Global Success
  - Tiếng Anh - Family and Friends
  - Tiếng Anh - iLearn Smart Start
  - Tiếng Anh - Explore Our World
  - Tiếng Anh - Phonics Smart
  - SBT Tiếng Anh - Global Success
  - SBT Tiếng Anh - Family and Friends
  - SBT Tiếng Anh - iLearn Smart Start
  - >> Xem thêm
- Lịch sử và Địa lí 5
  - SGK Lịch sử và Địa lí - Kết nối tri thức
  - SGK Lịch sử và Địa lí - Cánh diều
  - SGK Lịch sử và Địa lí - Chân trời sáng tạo
  - VBT Lịch sử và Địa lí - Kết nối tri thức
  - VBT Lịch sử và Địa lí - Cánh diều
  - Đề thi, đề kiểm tra Lịch sử và Địa lí - Kết nối tri thức
  - Đề thi, đề kiểm tra Lịch sử và Địa lí - Chân trời sáng tạo
  - Đề thi, đề kiểm tra Lịch sử và Địa lí - Cánh diều
- Khoa học 5
  - SGK Khoa học - Kết nối tri thức
  - SGK Khoa học - Chân trời sáng tạo
  - SGK Khoa học - Cánh diều
  - VBT Khoa học - Kết nối tri thức
  - VBT Khoa học - Chân trời sáng tạo
  - VBT Khoa học - Cánh diều
- Đạo đức 5
  - SGK Đạo đức - Kết nối tri thức
  - SGK Đạo đức - Chân trời sáng tạo
  - SGK Đạo đức - Cánh diều
  - VBT Đạo đức - Kết nối tri thức
  - VBT Đạo đức - Chân trời sáng tạo
  - VBT Đạo đức - Cánh diều
- Tin học 5
  - SGK Tin học - Cánh diều
  - SGK Tin học - Kết nối tri thức
  - SGK Tin học - Chân trời sáng tạo
  - VBT Tin học - Kết nối tri thức
  - VBT Tin học - Chân trời sáng tạo
  - VBT Tin học - Cánh diều
- HĐ trải nghiệm, hướng nghiệp 5
  - SGK Hoạt động trải nghiệm - Kết nối tri thức
  - SGK Hoạt động trải nghiệm - Cánh diều
  - SGK Hoạt động trải nghiệm - Chân trời sáng tạo Bản 1
  - SGK Hoạt động trải nghiệm - Chân trời sáng tạo Bản 2
  - VBT Hoạt động trải nghiệm - Kết nối tri thức
  - VBT Hoạt động trải nghiệm - Cánh diều
  - VBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
  - VBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
- Công nghệ 5
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Chân trời sáng tạo
  - SGK Công nghệ - Cánh diều
  - VBT Công nghệ - Kết nối tri thức
- Đề thi, đề kiểm tra 5
  - Đề thi vào lớp 6
  - Tổng hợp đề thi, đề kiểm tra
Lớp 4
- Toán học 4
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh diều
  - SGK Toán - Bình Minh
  - VBT Toán - Kết nối tri thức
  - Vở thực hành Toán
  - Trắc nghiệm Toán - Kết nối tri thức
  - Trắc nghiệm Toán - Cánh diều
  - >> Xem thêm
- Tiếng việt 4
  - Tiếng Việt - Kết nối tri thức
  - Tiếng Việt - Chân trời sáng tạo
  - Tiếng Việt - Cánh diều
  - VBT Tiếng Việt - Kết nối tri thức
  - Đề thi, đề kiểm tra Tiếng Việt - Kết nối tri thức
  - Đề thi, đề kiểm tra Tiếng Việt - Chân trời sáng tạo
  - Đề thi, đề kiểm tra Tiếng Việt - Cánh diều
  - Ôn hè Tiếng Việt
  - >> Xem thêm
- Tiếng Anh 4
  - Tiếng Anh - Global Sucess
  - Tiếng Anh - Family and Friends
  - Tiếng Anh - iLearn Smart Start
  - Tiếng Anh - Phonics Smart
  - Tiếng Anh - Explore Our World
  - SBT Tiếng Anh - Global Success
  - SBT Tiếng Anh - Family and Friends
  - SBT Tiếng Anh - iLearn Smart Start
  - >> Xem thêm
- Lịch sử và Địa lí 4
  - SGK Lịch sử và Địa lí - Kết nối tri thức
  - SGK Lịch sử và Địa lí - Chân trời sáng tạo
  - SGK Lịch sử và Địa lí - Cánh diều
  - VBT Lịch sử và Địa lí - Kết nối tri thức
  - VBT Lịch sử và Địa lí - Chân trời sáng tạo
  - VBT Lịch sử và Địa lí - Cánh diều
  - Đề thi, đề kiểm tra Lịch sử và Địa lí - Kết nối tri thức
  - Đề thi, đề kiểm tra Lịch sử và Địa lí - Chân trời sáng tạo
  - >> Xem thêm
- Khoa học 4
  - SGK Khoa học - Kết nối tri thức
  - SGK Khoa học - Chân trời sáng tạo
  - SGK Khoa học - Cánh diều
  - VBT Khoa học - Kết nối tri thức
  - VBT Khoa học - Chân trời sáng tạo
  - VBT Khoa học - Cánh diều
- Đạo đức 4
  - SGK Đạo đức - Kết nối tri thức
  - SGK Đạo đức - Chân trời sáng tạo
  - SGK Đạo đức - Cánh diều
  - VBT Đạo đức - Kết nối tri thức
  - VBT Đạo đức 4 - Chân trời sáng tạo
  - VBT Đạo đức - Cánh diều
- Tin học 4
  - SGK Tin học - Kết nối tri thức
  - SGK Tin học - Chân trời sáng tạo
  - SGK Tin học - Cánh diều
  - VBT Tin học - Kết nối tri thức
  - VBT Tin học - Chân trời sáng tạo
  - VBT Tin học - Cánh diều
- Công nghệ 4
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Chân trời sáng tạo
  - SGK Công nghệ - Cánh diều
  - VBT Công nghệ - Kết nối tri thức
  - VBT Công nghệ - Chân trời sáng tạo
  - VBT Công nghệ - Cánh diều
- HĐ trải nghiệm, hướng nghiệp 4
  - SGK Hoạt động trải nghiệm - Kết nối tri thức
  - SGK Hoạt động trải nghiệm - Cánh diều
  - SGK Hoạt động trải nghiệm - Chân trời sáng tạo Bản 1
  - SGK Hoạt động trải nghiệm - Chân trời sáng tạo Bản 2
  - VBT Hoạt động trải nghiệm - Kết nối tri thức
  - VBT Hoạt động trải nghiệm - Cánh diều
  - VBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 1)
  - VBT Hoạt động trải nghiệm - Chân trời sáng tạo (Bản 2)
- Âm nhạc 4
  - SGK Âm nhạc - Kết nối tri thức
  - SGK Âm nhạc - Chân trời sáng tạo
  - SGK Âm nhạc - Cánh diều
- Mỹ thuật 4
  - SGK Mĩ thuật - Kết nối tri thức
  - SGK Mĩ thuật - Cánh diều
  - SGK Mĩ thuật - Chân trời sáng tạo bản 1
  - SGK Mĩ thuật - Chân trời sáng tạo bản 2
- Giáo dục thể chất 4
  - SGK Giáo dục thể chất - Kết nối tri thức
  - SGK Giáo dục thể chất - Cánh diều
  - SGK Giáo dục thể chất - Chân trời sáng tạo
- Giáo dục địa phương 4
  - Tài liệu Giáo dục địa phương
- Đề thi, đề kiểm tra 4
  - Tổng hợp đề thi, đề kiểm tra
Lớp 3
- Toán học 3
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh diều
  - VBT Toán - Kết nối tri thức
  - Trắc nghiệm Toán - Kết nối tri thức
  - Trắc nghiệm Toán - Cánh diều
  - Trắc nghiệm Toán - Chân trời sáng tạo
  - Đề thi, đề kiểm tra Toán - Kết nối tri thức
  - >> Xem thêm
- Tiếng việt 3
  - Tiếng Việt - Kết nối tri thức
  - Tiếng Việt - Chân trời sáng tạo
  - Tiếng Việt - Cánh diều
  - VBT Tiếng Việt - Kết nối tri thức
  - VBT Tiếng Việt - Chân trời sáng tạo
  - VBT Tiếng Việt - Cánh diều
  - Đề thi, đề kiểm tra Tiếng Việt - Kết nối tri thức
  - Đề thi, đề kiểm tra Tiếng Việt - Chân trời sáng tạo
  - >> Xem thêm
- Tiếng Anh 3
  - Tiếng Anh - Global Success
  - Tiếng Anh - Family and Friends
  - Tiếng Anh - iLearn Smart Start
  - Tiếng Anh - Explore Our World
  - Tiếng Anh - Phonics Smart
  - SBT Tiếng Anh - Global Success
  - SBT Tiếng Anh - Family and Friends
  - SBT Tiếng Anh - iLearn Smart Start
  - >> Xem thêm
- Tự nhiên và xã hội 3
  - VBT Tự nhiên và xã hội - Cánh diều
  - Tự nhiên và xã hội - Kết nối tri thức
  - Tự nhiên và xã hội - Chân trời sáng tạo
  - Tự nhiên và xã hội - Cánh diều
  - VBT Tự nhiên và xã hội - Kết nối tri thức
  - VBT Tự nhiên và xã hội - Chân trời sáng tạo
- Đạo đức 3
  - SGK Đạo đức - Kết nối tri thức
  - SGK Đạo đức - Chân trời sáng tạo
  - SGK Đạo đức - Cánh diều
  - VBT Đạo đức - Kết nối tri thức
  - VBT Đạo đức - Cánh diều
  - VBT Đạo đức - Chân trời sáng tạo
- Tin học 3
  - SGK Tin học - Kết nối tri thức
  - SGK Tin học - Chân trời sáng tạo
  - SGK Tin học - Cánh diều
  - VBT Tin học - Kết nối tri thức
  - VBT Tin học - Chân trời sáng tạo
- HĐ trải nghiệm, hướng nghiệp 3
  - SGK Hoạt động trải nghiệm- Kết nối tri thức
  - SGK Hoạt động trải nghiệm- Chân trời sáng tạo
  - SGK Hoạt động trải nghiệm - Cánh diều
  - VBT Hoạt động trải nghệm - Kết nối tri thức
  - VBT Hoạt động trải nghiệm - Chân trời sáng tạo
  - VBT Hoạt động trải nghiệm - Cánh diều
- Công nghệ 3
  - SGK Công nghệ - Kết nối tri thức
  - SGK Công nghệ - Chân trời sáng tạo
  - SGK Công nghệ - Cánh diều
  - VBT Công nghệ - Kết nối tri thức
  - VBT Công nghệ - Chân trời sáng tạo
  - VBT Công nghệ - Cánh diều
- Âm nhạc 3
  - Âm nhạc - Kết nối tri thức
  - Âm nhạc - Chân trời sáng tạo
  - Âm nhạc - Cánh diều
- Giáo dục thể chất 3
  - SGK Giáo dục thể chất - Kết nối tri thức
  - SGK Giáo dục thể chất - Chân trời sáng tạo
  - SGK Giáo dục thể chất - Cánh diều
- Giáo dục địa phương 3
  - Tài liệu Giáo dục địa phương
Lớp 2
- Toán học 2
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Chân trời sáng tạo
  - SGK Toán - Cánh Diều
  - VBT Toán - KNTT
  - VBT Toán - CTST
  - Trắc nghiệm Toán - Kết nối tri thức
  - Trắc nghiệm Toán - Chân trời sáng tạo
  - Trắc nghiệm Toán - Cánh Diều
  - >> Xem thêm
- Tiếng việt 2
  - Tiếng Việt - Kết nối tri thức
  - Tiếng Việt - Chân trời sáng tạo
  - Tiếng Việt - Cánh Diều
  - Văn mẫu - Kết nối tri thức
  - Văn mẫu - Chân trời sáng tạo
  - Văn mẫu - Cánh diều
  - VBT Tiếng Việt - Kết nối tri thức
  - VBT Tiếng Việt - Chân trời sáng tạo
  - >> Xem thêm
- Tiếng Anh 2
  - Tiếng Anh - Kết nối tri thức
  - Tiếng Anh - Family and Friends
  - Tiếng Anh - iLearn Smart Start
  - Tiếng Anh - Phonics Smart
  - Tiếng Anh - English Discovery
  - Tiếng Anh - Explore Our World
  - Family & Friends Special
  - SBT Kết nối tri thức
  - >> Xem thêm
- Tự nhiên và xã hội 2
  - Tự nhiên và xã hội - Kết nối tri thức
  - Tự nhiên và xã hội - Chân trời sáng tạo
  - Tự nhiên và xã hội - Cánh diều
  - VBT Tự nhiên và xã hội - Kết nối tri thức
  - VBT Tự nhiên và xã hội - Cánh diều
  - VBT Tự nhiên và xã hội - Chân trời sáng tạo
- Đạo đức 2
  - SGK Đạo đức - Kết nối tri thức
  - SGK Đạo đức - Chân trời sáng tạo
  - SGK Đạo đức - Cánh Diều
  - VBT Đạo đức - Kết nối tri thức
  - VBT Đạo đức - Chân trời sáng tạo
  - VBT Đạo đức - Cánh Diều
- Âm nhạc 2
  - Âm nhạc 2 - Kết nối tri thức
  - Âm nhạc 2 - Chân trời sáng tạo
  - Âm nhạc 2 - Cánh diều
  - VBT Âm nhạc - Kết nối tri thức
  - VBT Âm nhạc - Chân trời sáng tạo
  - VBT Âm nhạc - Cánh diều
- Mỹ thuật 2
  - Mĩ thuật- Kết nối tri thức
  - Mĩ thuật- Chân trời sáng tạo
  - Mĩ thuật - Cánh Diều
- HĐ trải nghiệm, hướng nghiệp 2
  - VBT Hoạt động trải nghiệm - Chân trời sáng tạo
  - VTH Hoạt động trải nghiệm - Cánh Diều
  - VBT Hoạt động trải nghiệm - Kết nối tri thức
- Giáo dục địa phương 2
  - Tài liệu Giáo dục địa phương
Lớp 1
- Tiếng việt 1
  - Đề thi, kiểm tra Tiếng Việt
  - SGK Tiếng Việt - Kết nối tri thức
  - SGK Tiếng Việt - Chân trời sáng tạo
  - SGK Tiếng Việt - Cánh diều
- Toán học 1
  - SGK Toán - Kết nối tri thức
  - SGK Toán - Cánh diều
  - SGK Toán - Chân trời sáng tạo
  - Trắc nghiệm Toán
- Tiếng Anh 1
  - Chứng chỉ Cambridge Pre A1 Starters
- Truyện cổ tích 1
  - Truyện cổ tích
- Tự nhiên và xã hội 1
  - Tự nhiên & xã hội
  - VBT Tự nhiên & xã hội
- Đạo đức 1
  - VBT Đạo Đức
- Giáo dục địa phương 1
  - Tài liệu Giáo dục địa phương
Công cụ
- Ngữ văn
  - Từ điển tiếng việt
  - Dẫn chứng nghị luận xã hội
  - Từ đồng nghĩa, trái nghĩa
  - Thành ngữ Việt Nam
  - Ca dao, tục ngữ
  - Chính tả tiếng Việt
  - Từ láy
  - Kho truyện
  - Luyện kĩ năng đọc hiểu
  - >> Xem thêm
- Tiếng Anh
  - Động từ bất quy tắc
  - Cụm động từ (Phrasal verbs)

PHẦN ĐẠI SỐ
- CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC
  - 100 bài tập Nhân đơn thức với đa thức, nhân đa thức với đa thức
  - 100 bài tập Những hằng đẳng thức đáng nhớ
  - 100 bài tập Phân tích đa thức thành nhân tử
  - 100 bài tập Chia đơn thức cho đơn thức, chia đa thức cho đơn thức
  - 100 bài tập Chia đa thức một biến đã sắp xếp
  - 100 bài tập Ôn tập chương 1: Phép nhân và phép chia các đa thức
- CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
  - 100 bài tập Tính chất cơ bản của phân thức
  - 100 bài toán Rút gọn phân thức
  - 100 bài tập Qui đồng mẫu thức nhiều phân thức
  - 100 bài tập Phép cộng và phép trừ các phân thức đại số
  - 100 bài tập Phép nhân, phép chia các phân thức đại số
  - 100 bài tập Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
  - 100 bài tập Ôn tập chương 2: Phân thức đại số
PHẦN HÌNH HỌC
- CHƯƠNG 1: TỨ GIÁC
  - 100 bài tập về hình thang, hình thang cân
  - 100 bài tập Đường trung bình của tam giác, của hình thang
  - 100 bài tập về Hình bình hành
  - 100 bài tập về Hình chữ nhật
  - 100 bài tập về Hình thoi
  - 100 bài tập về Hình vuông
  - 100 bài tập Ôn tập chương 1: Tứ giác

Trắc nghiệm Toán 8 có đáp án và lời giải chi tiết 100 bài tập Đường trung bình của tam giác, của hình thang

20 bài tập vận dụng Đường trung bình của tam giác, của hình thang

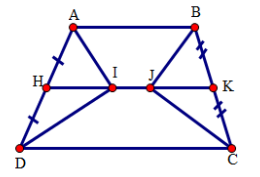
Làm đề thi

Câu hỏi 1 :

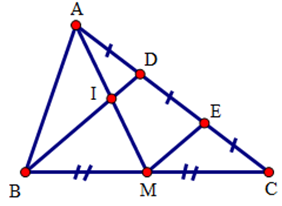
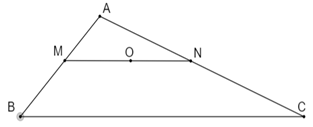
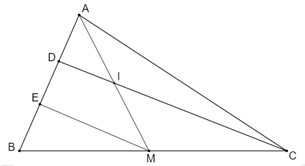
Cho tam giác \(ABC\) , điểm \(D\) thuộc cạnh \(AC\) sao cho \(AD=\frac{1}{2}DC\). Gọi \(M\) là trung điểm của \(BC,I\) là giao điểm của \(BD\) và \(AM\). Chứng minh rằng \(AI=IM\).

Phương pháp giải:

Phương pháp:

Sử dụng dấu hiệu nhận biết để chứng minh các đoạn thẳng là đường trung bình của tam giác. Từ đó dùng các tính chất của đường trung bình để suy ra điều cần chứng minh.

Lời giải chi tiết:

Gọi \(E\) là trung điểm của \(DC\) .

Xét tam giác \(BDC\) có: \(BM=MC,DE=EC\) nên \(ME\) là đường trung bình của tam giác\(BDC\) . Suy ra \(BD//ME\) hay \(DI//EM\) .

Xét tam giác \(AME\) có \(AD=DE,DI//EM\) nên \(AI~=IM\) (đpcm)

Đáp án - Lời giải

Câu hỏi 2 :

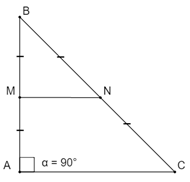
Cho tam giác ABC vuông tại A, \(AB = 12cm,BC = 13cm\). Gọi M, N là trung điểm AB, BC

a) Chứng minh MN vuông góc với AB. b) Tính độ dài đoạn MN.

A \(b)\,\,MN = 2cm\)
B \(b)\,\,MN = 2,5cm\)
C \(b)\,\,MN = 3cm\)
D \(b)\,\,MN = 3,5cm\)

Đáp án: B

Phương pháp giải:

Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy

Áp dụng định lý Py-ta-go: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Lời giải chi tiết:

a) Chứng minh \(MN \bot AB\)

MN là đường trung bình của \(\Delta ABC\,\,\,\left( {gt} \right)\)

\( \Rightarrow MN//AC\) (định lí 2)

Mà \(AC \bot AB\) (\(\Delta ABC\) vuông tại A)

Do đó \(MN \bot AB\). (từ song song đến vuông góc)

b) Tính độ dài MN.

Áp dụng đinh lý Py-ta-go cho \(\Delta ABC\) ta có:

\(\begin{array}{l}B{C^2} = A{C^2} + A{B^2}\\ \Leftrightarrow A{C^2} = B{C^2} - A{B^2}\\ \Leftrightarrow A{C^2} = {13^2} - {12^2}\\ \Leftrightarrow A{C^2} = 169 - 144 = 25\\ \Rightarrow AC = 5cm.\end{array}\)

Do \(MN = \frac{{AC}}{2}\) (MN là đường trung bình \(\Delta ABC\))

\( \Rightarrow MN = \frac{5}{2} = 2,5\,\,cm.\)

Chọn B.

Đáp án - Lời giải

Câu hỏi 3 :

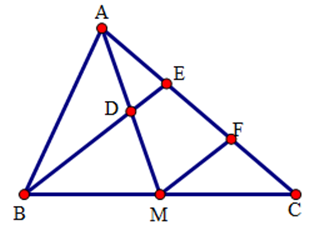
Cho tam giác \(ABC\), đường trung tuyến \(AM\). Gọi \(D\) là trung điểm của \(AM,E\) là giao điểm của \(BD\) và \(AC,F\) là trung điểm của \(EC\). Chọn câu đúng trong các câu sau:

A \(AE=\frac{1}{2}EC\)
B \(AE=2EC\)
C \(FC=AF\)
D \(MF=BE\)

Đáp án: A

Phương pháp giải:

Phương pháp:

Sử dụng các dấu hiệu nhận biết đường trung bình để chứng minh các đoạn thẳng là đường trung bình của tam giác. Từ đó rút ra các mối liện hệ giữa các đoạn thẳng.

Lời giải chi tiết:

Hướng dẫn giải chi tiết

Xét tam giác \(BEM\) có \(BM=MC,EF=FC\) nên \(MF\) là đường trung bình của tam giác \(BEC\). Do đó \(MF//BE\).

Xét tam giác \(AMF\) có \(AD=DM,DE//MF\) nên \(DE\) là đường trung bình của tam giác \(AMF\). Do đó \(AE=EF\).

Do đó \(AE=EF=FC\) nên \(AE=\frac{1}{2}EC\).

Chọn A

Đáp án - Lời giải

Câu hỏi 4 :

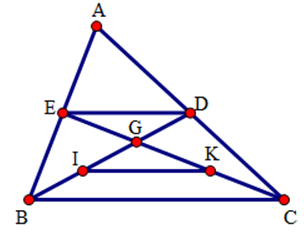
Cho tam giác \(ABC\), các đường trung tuyến \(BD\) và \(CE\) cắt nhau ở \(G\). Gọi \(I,K\) theo thứ tự là trung điểm của \(GB,GC\). Trong các câu sau câu nào đúng

A \(DE//IK\)
B \(DE=IK\)
C Cả A và B đều đúng
D Cả A và B đều sai.

Đáp án: C

Phương pháp giải:

Phương pháp:

Sử dụng dấu hiệu nhận biết để chứng minh các đường thẳng lần lượt là các đường trung bình của các tam giác tương ứng. Sau đó sử dụng tính chất của các đường trung bình để suy ra các mỗi liên hệ giữa các đoạn thẳng.

Lời giải chi tiết:

Hướng dẫn giải chi tiết

Vì tam giác \(ABC\) có \(AE=EB,AD=DC\) nên \(ED\) là đường trung bình, do đó \(ED//BC,ED=\frac{1}{2}BC\(.

Tương tự tam giác \(GBC\) có \(GI=IB,GK=KC\) nên \(IK\) là đường trung bình, do đó \(IK//BC,IK=\frac{1}{2}BC\).

Suy ra \(ED//IK\) (cùng song song với \(BC\))

\(ED=IK\) (cùng bằng \(\frac{1}{2}BC\))

Chọn C

Đáp án - Lời giải

Câu hỏi 5 :

Cho tam giác \(ABC\) với \(AC>AB\). Gọi \(M,N\) lần lượt là trung điểm của \(BC\) và \(AB\). Từ \(M\) và \(C\) kẻ đường vuông góc với phân giác trong của góc \(A\), các đường này lần lượt cắt tia \(AB\) tại \(P\) và \(E\).

a) Chứng minh rằng \(AP=\frac{AB+AC}{2}\)

b) Chứng minh \(\Delta PNM\) là tam giác cân.

c) So sánh \(PN\) và \(AC\)

Phương pháp giải:

Phương pháp:

a) Chứng minh \(P\) là trung điểm của \(BE\) dựa vào đường trung bình rồi suy ra \(AP=\frac{AB+AE}{2}\).

Chứng minh \(\Delta ACE\) cân tại \(A\) suy ra \(AE=AC\Rightarrow \) đpcm.

b) Chứng minh \(\Delta NPM\) cân tại \(N\) bằng cách sử dụng tính chất đường trung bình và tính chất tam giác cân.

c) Chứng minh \(PN=\frac{1}{2}AC\).

Lời giải chi tiết:

a) Ta có \(AP=AB+BP\)

\(AP=AEPE\)

Do đó \(2AP=AB+AE+BPPE\text{ }\left( 1 \right)\)

Trong tam giác \(BCE\) ta có :\(BM=MC\) và \(MP//CE\) (cùng vuông góc với tia phân giác \(Ax\)) nên suy ra \(P\) là trung điểm của \(BE\) và ta có \(BP=PE\) .

Mặt khác tam giác \(ACE\) cân tại \(A\) vì có phân giác trong của góc \(A\) cũng là đường cao. Do đó \(AE=AC\) .

Vậy (1) cho ta \(2AP=AB+AC\) hay \(\text{AP =}\frac{AB+AC}{2}\) (đpcm)

b) Đường thẳng \(MP\) cắt \(AC\) tại \(Q\) . Ta có tam giác \(APQ\) cân tại \(A\) vì phân giác trong của góc \(A\) cũng là đường cao, nên ta có \(\widehat{APM}=\widehat{AQP}\) .

Mà \(\widehat{NMP}=\widehat{AQP}\) (hai góc đồng vị)

Do đó \(\widehat{APM}=\widehat{NMP}\)

Suy ra tam giác \(MNP\) cân tại \(N\).

Suy ra \(PN=MN\)

c) Ta có \(MN=\frac{1}{2}AC\) ( đường trung bình của tam giác \(ABC\))

Vậy \(PN=\frac{1}{2}AC\).

Đáp án - Lời giải

Câu hỏi 6 :

Độ dài đường trung bình của hình thang là \(16cm\); hai đáy tỉ lệ với \(3\) và \(5\) thì độ dài hai đáy là :

A \(12cm\) và \(20cm\)
B \(6cm\) và \(10\text{ }cm\)
C \(3cm\) và \(5cm\)
D Đáp số khác

Đáp án: A

Phương pháp giải:

Phương pháp: Sử dụng định lí đường trung bình của hình thang và tính chất dãy tỉ số bằng nhau.

Lời giải chi tiết:

Cách giải: Gọi \(a\) và \(b\) lần lượt là độ dài hai đáy nhỏ, đáy lớn của hình thang.

Theo định lí đường trung bình của hình thang suy ra \(a+b=2.16=32(cm)\).

Mặt khác theo bài ra \(a\) và \(b\) tỉ lệ với \(3\) và \(5\) nên ta có: \(\frac{a}{3}=\frac{b}{5}\) .

Theo tính chất của dãy tỉ số bằng nhau ta có:

\(\begin{align} & \frac{a}{3}=\frac{b}{5}=\frac{a+b}{3+5}=\frac{32}{8}=4 \\ & \Rightarrow a=4.3=12(cm) \\ & \Rightarrow b=4.5=20(cm) \\\end{align}\)

Vậy độ dài \(2\) đáy của hình thang là \(12cm,\text{ }20cm\) .

Chọn A

Đáp án - Lời giải

Câu hỏi 7 :

Một hình thang cân có cạnh bên là \(2,5cm\) , đường trung bình là \(3cm\). Chu vi của hình thang đó là:

A \(8cm\)
B \(8,5cm\)
C \(11,5cm\)
D \(11cm\)

Đáp án: D

Phương pháp giải:

Phương pháp: Dựa vào định lí đường trung bình của hình thang ta tính được tổng hai đáy của hình thang. Từ đó tính được chu vi của hình thang.

Lời giải chi tiết:

Cách giải: Từ định lí đường trung bình của hình thang suy ra độ dài tổng hai đáy của hình thang bằng hai lần độ dài đường trung bình của hình thang và bằng: \(3.2=6(cm)\)

Mà đây là hình thang cân nên có chu vi của hình thang là: \(6+2,5.2=11(cm)\) .

Chọn D.

Đáp án - Lời giải

Câu hỏi 8 :

Cho hình thang \(ABCD\left( AB//CD \right)\), \(M\) là trung điểm của \(AD,\text{ }N\) là trung điểm của \(BC\) . Gọi \(I,\text{ }K\) theo thứ tự là giao điểm của \(MN\) với \(BD,\text{ }AC\) . Cho biết \(AB=6cm,CD=14cm\) . Tính các độ dài \(MI,\text{ }IK,\text{ }KN\).

A \(\begin{array}{l}MI = 3\,\,cm\\IK = 4\,cm\\KN = 3\,cm\end{array}\)
B \(\begin{array}{l}MI = 4\,\,cm\\IK = 4\,cm\\KN = 3\,cm\end{array}\)
C \(\begin{array}{l}MI = 3\,\,cm\\IK = 4\,cm\\KN = 4\,cm\end{array}\)
D \(\begin{array}{l}MI = 3\,\,cm\\IK = 3\,cm\\KN = 3\,cm\end{array}\)

Đáp án: A

Phương pháp giải:

Sử dụng định lí đường trung bình của hình thang ta tính được \(MN\), sử dụng định lí đường trung bình của tam giác ta tính được \(MK,MI\).

Từ đó tính được \(IK,\text{ }KN\).

Lời giải chi tiết:

Xét hình thang \(ABCD\) có: \(M\) là trung điểm của \(AD;\text{ }N\) là trung điểm của \(BC\)

\(\Rightarrow \) \(MN\) là đường trung bình của hình thang \(ABCD\) \(\Rightarrow \left\{ \begin{align} & MN=\frac{AB+CD}{2}=\frac{6+14}{2}=10(cm) \\ & MN//AB//CD \\\end{align} \right.\)

Xét \(\Delta ADC\) có: \(AM\text{ }=\text{ }MD,\text{ }MK\text{ }//\text{ }DC\) nên \(AK=KC\) (định lí đường trung bình của tam giác)

\(\Rightarrow \)\(MK\) là đường trung bình của \(\Delta ADC\Rightarrow MK=\frac{DC}{2}=\frac{14}{2}=7\left( cm \right)\)

Xét \(\Delta ABD\) có: \(AM\text{ }=\text{ }MD,\text{ }MI\text{ }//\text{ }AB\) nên \(BI=ID\) (định lí đường trung bình của tam giác)

\(\Rightarrow \) \(MI\) là đường trung bình của \(\Delta ABD\Rightarrow MI=\frac{AB}{2}=\frac{6}{2}=3\left( cm \right)\)

\(\begin{align} & \Rightarrow IK=MK-MI=7-3=4\,(cm) \\ & KN=MN-MK=10-7=3\,(cm) \\\end{align}\)

Đáp án - Lời giải

Câu hỏi 9 :

Tính độ dài đường trung bình của hình thang cân, biết rằng hai đường chéo vuông góc với nhau và đường cao của nó bằng \(10cm\).

A \(8\,cm\)
B \(15\,cm\)
C \(10\,cm\)
D \(12\,cm\)

Đáp án: C

Phương pháp giải:

Ta đi chứng minh đường trung bình của hình thang cân \(ABCD\) bằng đường cao đi qua giao điểm của hai đường chéo của hình thang

Sử dụng định lí đường trung bình của hình thang để tính

Lời giải chi tiết:

Xét hình thang cân \(ABCD\left( AB//CD \right)\) , hai đường chéo \(AC\) và \(BD\) vuông góc với nhau tại \(O,\text{ }MN\) là đường trung bình của hình thang \(ABCD.\)

Qua \(O\) kẻ đường thẳng vuông góc với \(AB\) tại \(E,\) với \(CD\) tại \(F.\)

Xét \(\Delta ADC\) và \(\Delta BCD\) có:

\(AD=BC\) (gt)

DC cạnh chung

\(\widehat{ADC}=\widehat{BCD}\) (gt)

\(\Rightarrow \Delta ADC=\Delta BCD(c.g.c)\Rightarrow \widehat{ACD}=\widehat{BDC}\) (hai góc tương ứng)

\(\Rightarrow \Delta OCD\) cân tại \(O \)

\(\Rightarrow OC=OD\) (tính chất tam giác cân).

Mà \(AC=BD\) nên \(OA=OB\Rightarrow \Delta OAB\) cân tại \(O\).

Lại có \(\widehat{AOB}=90{}^\circ \) (do \(AB\) vuông góc với \(CD\)) nên \(\Delta AOB\) vuông cân tại \(O\) nên \(OE=\frac{AB}{2}\).

Tương tự: tam giác \(DOC\) vuông cân tại \(O\) nên \(FO=\frac{CD}{2}\)

Do đó \(FE=\frac{AB+CD}{2}\)

\(MN\) là đường trung bình của hình thang \(ABCD\) nên \(MN=\frac{AB+CD}{2}\)

\(\Rightarrow MN=FE=10cm\)

Đáp án - Lời giải

Câu hỏi 10 :

Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai.

Phương pháp giải:

Sử dụng định lí đường trung bình của hình thang, đường trung bình của tam giác để chứng minh.

Lời giải chi tiết:

Xét hình thang \(ABCD\) có \(AB//CD,AE=ED,FE//AB//CD\), suy ra \(BF=FC\) (định lí đường trung bình của hình thang).

Xét \(\Delta ADC\) có \(AE=ED,EK//DC\), suy ra \(AK=KC\) (định lí đường trung bình của \(\Delta BDC\)) .

Xét \(\Delta ABD\) có \(AE=ED,EI//AB\), suy ra \(BI=ID\) (định lí đường trung bình của \(\Delta ABC\)).

Do đó \(EF\) đi qua trung điểm của \(BC,\,AC,\,BD\).

Đáp án - Lời giải

Câu hỏi 11 :

Độ dài hai đáy của một hình thang lần lượt là 3cm và 7cm, thì độ dài đường trung bình của hình thang đó bằng:

A 10 cm
B 5 cm
C 4 cm
D 2 cm

Đáp án: B

Phương pháp giải:

Độ dài đường trung bình của hình thang bằng nửa tổng độ dài hai đấy.

Lời giải chi tiết:

Độ dài đường trung bình của hình thang là: (3 + 7) : 2 = 5(cm)

Đáp án - Lời giải

Câu hỏi 12 :

Cho tam giác ABC. Từ điểm O trong tam giác đó kẻ đường thẳng song song với BC cắt cạnh AB ở M, cắt cạnh AC ở N.

a) Tứ giác BMNC là hình gì? Vì sao?

b) Tìm điều kiện của DABC để tứ giác BMNC là hình thang cân?

Phương pháp giải:

Áp dụng định nghĩa của hình thang: hình thang là tứ giác có 2 cạnh đối song song.

Áp dụng định nghĩa của hình thang cân: hình thang cân là hình thang có 2 góc kề một đáy bằng nhau

Lời giải chi tiết:

a) Tứ giác BMNC là hình gì? Vì sao?

Theo đề bài ta có: \(MN//BC.\)

\( \Rightarrow BMNC\) là hình thang. (định nghĩa)

b) Tìm điều kiện của DABC để tứ giác BMNC là hình thang cân?

Theo câu a) ta có: \(BMNC\) là hình thang có hai đáy \(MN,\,\,BC.\)

\( \Rightarrow BMNC\) là hình thang cân \( \Leftrightarrow \angle B = \angle C.\)

\( \Rightarrow \Delta ABC\) là tam giác cân tại \(A.\)

Vậy để \(BMNC\) là hình thang cân thì \(\Delta ABC\) là tam giác cân tại \(A.\)

Đáp án - Lời giải

Câu hỏi 13 :

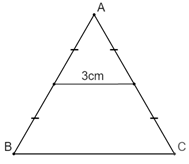
Cho tam giác ABC đều và có độ dài một đường trung bình là \(3cm\). Ta tính được chu vi tam giác ABC là

A \(36cm\)
B \(9cm\)
C \(12cm\)
D \(18cm\)

Đáp án: D

Phương pháp giải:

Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Lời giải chi tiết:

Do đường trung bình của \(\Delta ABC\) bằng \(3cm\), nên độ dài BC là: \(BC = 2 \times 3 = 6cm\)

Mà \(\Delta ABC\) đều nên \(BC = AC = AB = 6cm\)

Vậy chu vi \(\Delta ABC\) là :\(BC + AC + AB = 6 + 6 + 6 = 18cm\)

Chọn D.

Đáp án - Lời giải

Câu hỏi 14 :

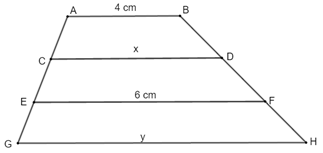
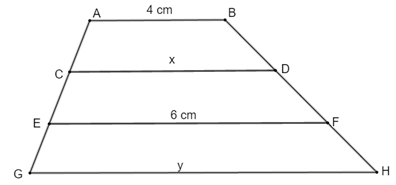
Cho hình vẽ sau:

Biết \(AC = CE = EG\),\(BD = DF = FH\) và \(AB//CD//EF//GH.\) Khi tính \(x\) và \(y,\) khẳng định nào dưới đây là đúng?

A \(x = 5cm,y = 7cm\)
B \(x = 5cm,y = 8cm\)
C \(x = 12cm,y = 18cm\)
D \(x = 12cm,y = 20cm\)

Đáp án: A

Phương pháp giải:

Áp dụng định lý 2 đường trung bình của hình thang: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Lời giải chi tiết:

+) Xét hình thang ABFE có: \(\left\{ \begin{array}{l}AB//CD//EF\\AC = CE\\BD = DF\end{array} \right. \Rightarrow \) CD là đường trung bình của hình thang ABFE (định nghĩa)

\( \Rightarrow x = CD = \frac{{AB + EF}}{2}\)\( = \frac{{4 + 6}}{2} = \frac{{10}}{2} = 5\,\,cm\)

+) Xét hình thang CDHG có: \(\left\{ \begin{array}{l}CD//EF//GH\\CE = EG\\DF = FH\end{array} \right. \Rightarrow \) EF là đường trung bình của hình thang CDHG (định nghĩa)

\(\begin{array}{l} \Rightarrow EF = \frac{{CD + GH}}{2} \Leftrightarrow 6 = \frac{{5 + y}}{2}\\ \Leftrightarrow 12 = 5 + y\,\, \Leftrightarrow y = 7\,\,cm\end{array}\)

Vậy \(x = 5cm,\,\,y = 7cm.\)

Chọn A.

Đáp án - Lời giải

Câu hỏi 15 :

Cho tam giác ABC có trung tuyến AM, trên đoạn AB lấy 2 điểm D và E sao cho\(AD = DE = EB\). Gọi I là giao điểm CD và AM. Chứng minh I là trung điểm AM.

Phương pháp giải:

Áp dụng định lý 1 đường trung bình của tam giác: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Lời giải chi tiết:

Xét \(\Delta BDC\) ta có: \(M,\,\,E\) lần lượt là trung điểm các cạnh \(BC,\,\,BD\)

\( \Rightarrow ME\) là đường trung bình của \(\Delta BDC.\) (định nghĩa)

\( \Rightarrow ME//CD.\)

Xét \(\Delta AEM\) ta có: \(D\) là trung điểm của \(AE\)

\(DE//ME\,\,\,\left( {DC//ME} \right)\)

\( \Rightarrow I\) là trung điểm của \(AM.\) (định lý đảo)

Đáp án - Lời giải

Câu hỏi 16 :

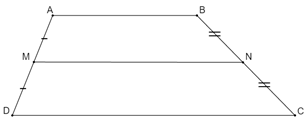
Cho hình thang ABCD (AB//CD); M và N là trung điểm AD và BC. Cho biết\(CD = 4cm,MN = 3cm\). Tính độ dài đoạn thẳng AB.

A \(AB = 2cm\)
B \(AB = 1,5cm\)
C \(AB = 3cm\)
D \(AB = 2,5cm\)

Đáp án: A

Phương pháp giải:

Áp dụng định lý 2 đường trung bình của hình thang: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Lời giải chi tiết:

Ta có: \(M,\,\,N\) lần lượt là trung điểm của \(AD\) và \(BC\)

\( \Rightarrow MN\) là đường trung bình của hình thang \(ABCD\) (định nghĩa)

\(\begin{array}{l} \Rightarrow MN = \frac{{AB + CD}}{2} \Leftrightarrow 3 = \frac{{AB + 4}}{2}\\ \Leftrightarrow AB + 4 = 6 \Leftrightarrow AB = 2\,\,cm.\end{array}\)

Chọn A.

Đáp án - Lời giải

Câu hỏi 17 :

Độ dài đường trung bình của hình thang là \(22,5cm\). Tỉ số hai đáy của hình thang là \(\frac{1}{2}\) .Tính độ dài hai đáy của hình thang.

A \(12cm\) và \(24cm\)
B \(14cm\) và \(28cm\)
C \(15cm\) và \(30cm\)
D \(16cm\) và \(32cm\)

Đáp án: C

Phương pháp giải:

Áp dụng định lý 2 đường trung bình của hình thang: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Lời giải chi tiết:

Gọi hai đáy của hình thang có độ dài là: \(x,\,\,y\,\,\,\left( {y > x > 0} \right).\)

\( \Rightarrow \frac{{x + y}}{2} = 22,5 \Leftrightarrow x + y = 45\) (định lý 2)

Theo đề bài ta có: \(\frac{x}{y} = \frac{1}{2}\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\begin{array}{l}\frac{x}{1} = \frac{y}{2} = \frac{{x + y}}{{1 + 2}} = \frac{{45}}{3} = 15\\ \Rightarrow \left\{ \begin{array}{l}x = 1.15 = 15\,\,cm.\\y = 2.15 = 30\,\,\,cm.\end{array} \right.\end{array}\)

Chọn C.

Đáp án - Lời giải

Câu hỏi 18 :

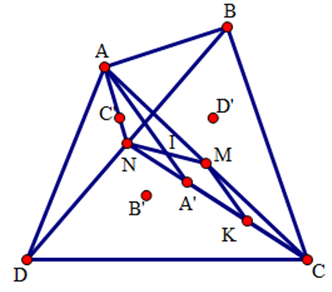
Cho tứ giác lồi \(ABCD,\) gọi \(A',\,B',\,C',\,D'\) lần lượt là trọng tâm của các tam giác \(BCD, \,ACD,\,ABD,\,ABC\) và \(M,\,N\) lần lượt là trung điểm của các đoạn thẳng \(AC,\,BD.\)

Chứng minh rằng các đường thẳng \(AA',\,BB',\,CC',\,DD'\) và \(MN\) đồng quy.

Phương pháp giải:

Dựa vào hình vẽ ta dự đoán \(AA',BB',CC',DD',MN\) sẽ đồng quy tại trung điểm của \(MN\). Gọi \(I\) là giao điểm của \(AA'\) và \(MN\) ta sẽ chứng minh \(I\) là trung điểm của \(MN\).

Ta dùng kiến thức về đường trung bình của tam giác và điểm \(K\) là trung điểm của \(A'C\) sẽ giúp ta giải bài toán.

Lời giải chi tiết:

Gọi \(I\) là giao điểm của \(AA'\) và \(MN,K\) là trung điểm của đoạn \(A'C\) .

Do \(A'\) là trọng tâm của tam giác \(BCD\) nên suy ra \(CK=KA=A'N\).

Tam giác \(AA'C\) có \(AM=MC\left( gt \right),CK=KA'\) suy ra \(MK\) là đường trung bình của tam giác \(AA'C.\)

Suy ra \(MK//AA'.\)

Tam giác \(NMK\) có \(IA'//MK\) và \(KA'=\text{ }A'N\) nên \(MI=IN\) .

Vậy \(I\) là trung điểm của \(MN,\) suy ra \(AA'\) đi qua trung điểm \(I\) của \(MN.\)

Chứng minh tương tự ta cũng có \(BB',CC',DD'\) đi qua \(I\).

Vậy các đường thẳng \(AA',\,BB',\,CC',\,DD',\,MN\) đồng quy.

Đáp án - Lời giải

Câu hỏi 19 :

Cho hình thang \(ABCD\left( AB//CD \right),\) hai đường phân giác của góc \(A\) và góc \(D\) cắt nhau tại \(I,\) hai đường phân giác của góc \(B\) và góc \(C\) cắt nhau tại \(J.\) Gọi \(H\) là trung điểm của \(AD,\text{ }K\) là trung điểm của \(BC\) . Cho biết \(AB=AD=10cm,\,BC=12cm,\,CD=20cm.\) Tính độ dài các đoạn \(HI,\text{ }IJ\) và \(JK.\)

A \(\begin{array}{l}HI = 5\,\,cm\\IJ = 3\,\,cm\\JK = 6\,cm\end{array}\)
B \(\begin{array}{l}HI = 5\,\,cm\\IJ = 4\,\,cm\\JK = 3\,cm\end{array}\)
C \(\begin{array}{l}HI = 3\,\,cm\\IJ = 4\,\,cm\\JK = 6\,cm\end{array}\)
D \(\begin{array}{l}HI = 5\,\,cm\\IJ = 4\,\,cm\\JK = 6\,cm\end{array}\)

Đáp án: D

Phương pháp giải:

Sử dụng định lí đường trung bình của hình thang để tính \(HK\).

Sau đó ta đi chứng minh bốn điểm \(H,\,I,\,J,\,K\) thẳng hàng từ đó tính được \(HI,\,J,\,IK\).

Lời giải chi tiết:

Xét hình thang \(ABCD\) có: \(H\) là trung điểm của \(AD,\text{ }K\) là trung điểm của \(BC\) nên \(KH\) là đường trung bình của hình thang \(ABCD\).

Suy ra \(\left\{ \begin{align} & KH\parallel CD(1) \\ & HK=\frac{AB+CD}{2}=\frac{10+20}{2}=15cm \\\end{align} \right.\)

Vì \(AI\) và \(DI\) là hai tia phân giác của góc \(A\) và góc \(D\) nên ta có:\(\widehat{IAD}+\widehat{IDA}=\frac{\widehat{A}+\widehat{D}}{2}=\frac{180{}^\circ }{2}=90{}^\circ \) .

Xét \(\Delta AID\) có: \(\widehat{AID}=180{}^\circ -\left( \widehat{IAD}+\widehat{IDA} \right)=180{}^\circ -90{}^\circ =90{}^\circ \) . Suy ra \(\Delta AID\) vuông tại \(I\). Lại có \(IH\) là đường trung tuyến ứng với cạnh huyền \(AD\) của tam giác vuông \(AID\) nên \(HI=HD\) .

Do đó tam giác \(HID\) cân tại \(H\) nên\(\widehat{HID}=\widehat{HDI}\) .

Mà \(\widehat{HDI}=\widehat{IDC}\Rightarrow \widehat{HID}=\widehat{IDC}\Rightarrow HI\parallel DC(2)\) .

Từ (1) và (2) suy ra \(H,\text{ }I,\text{ }K\) thẳng hàng hay điểm \(I\) thuộc đường thẳng \(HK\).

Tương tự điểm \(J\) thuộc đường thẳng \(HK\). Do đó bốn điểm \(H,\text{ }I,\text{ }J,\text{ }K\) thẳng hàng.

\(\begin{align} & IH=\frac{AD}{2}=\frac{10}{2}=5cm \\ & JK=\frac{BC}{2}=\frac{12}{2}=6cm \\ & \Rightarrow \text{IJ}=HK-IH-JK=15-5-6=4cm \\\end{align}\)

Đáp án - Lời giải

Câu hỏi 20 :

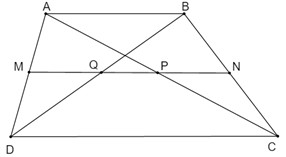
Cho hình thang ABCD (AB//CD). Gọi M, N, P, Q lần lượt là trung điểm AD, BC, AC, BD.

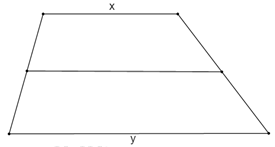
a) Chứng minh M, N, P, Q thẳng hàng. b) Giả sử \(AB < CD\). Chứng minh \(PQ = \frac{{DC - AB}}{2}\)

Phương pháp giải:

Áp dụng định lý 2 đường trung bình của hình thang: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy

Lời giải chi tiết:

a) Chứng minh M, N, P, Q thẳng hàng.

Xét hình thang ABCD ta có:

M, N lần lượt là trung điểm của AD và BC

\( \Rightarrow MN\) là đường trung bình của hình thang ABCD.

\( \Rightarrow MN//AB//CD\) (tính chất) (1)

Xét \(\Delta ADB\) ta có:

M, Q lần lượt là trung điểm của AD và BD

\( \Rightarrow MQ\) là đường trung bình của \(\Delta ADB\) (định nghĩa).

\( \Rightarrow MQ//AB\) (tính chất) (2)

Xét \(\Delta ABC\) ta có:

N, P lần lượt là trung điểm của BC và AC

\( \Rightarrow NP\) là đường trung bình của \(\Delta ABC\) (định nghĩa)

\( \Rightarrow NP//AB\) (tính chất) (3)

Từ (1), (2) và (3) ta có: \(MN//MQ//NP//AB\)

\( \Rightarrow M,\,\,N,\,\,P,\,\,\,Q\) thẳng hàng. (đpcm)

b) Giả sửa \(AB < CD.\) Chứng minh \(PQ = \frac{{DC - AB}}{2}.\)

Ta có: \(MQ\) là đường trung bình của \(\Delta ADB\)

\( \Rightarrow MQ = \frac{1}{2}AB.\)

\(NP\) là đường trung bình của \(\Delta ABC\)

\( \Rightarrow NP = \frac{1}{2}AB.\)

\( \Rightarrow MQ + NP = \frac{1}{2}AB + \frac{1}{2}AB = AB.\)

\(MN\) là đường trung bình của hình thang \(ABCD\)

\( \Rightarrow MN = \frac{{AB + CD}}{2}.\)

Lại có: \(PQ = MN - \left( {MQ + PN} \right)\)

\( \Rightarrow PQ = \frac{{AB + CD}}{2} - AB = \frac{{CD - AB}}{2}\,\,\,\left( {dpcm} \right)\)

Đáp án - Lời giải

Xem thêm

15 bài tập cơ bản Đường trung bình của tam giác, của hình thang

15 bài tập cơ bản Đường trung bình của tam giác, của hình thang có đáp án và lời giải chi tiết

Xem chi tiết

>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link