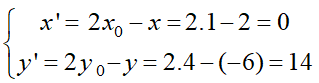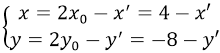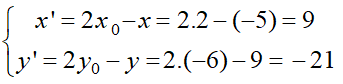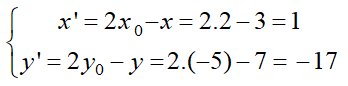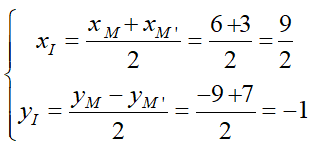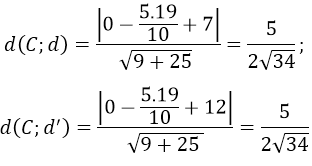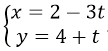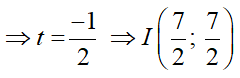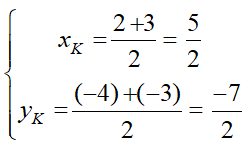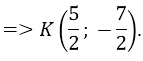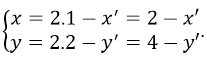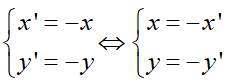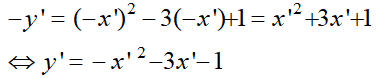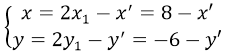20 Câu Trắc Nghiệm Toán Hình 11: Phép đối Xứng Tâm (Có đáp án)

Nội dung bài viết

1. Bộ 20 câu trắc nghiệm Toán hình 11: Phép đối xứng tâm

Để giúp các em học sinh lớp 11 học tập hiệu quả môn Toán, chúng tôi đã tổng hợp 20 câu trắc nghiệm Toán hình 11: Phép đối xứng tâm, chắc chắn các em sẽ rèn luyện kỹ năng giải Toán một cách nhanh và chính xác nhất. Mời các em học sinh và thầy cô tham khảo tài liệu: 20 câu trắc nghiệm Toán 11: Phép đối xứng tâm tại đây.

Bộ 20 câu trắc nghiệm Toán hình 11: Phép đối xứng tâm

Câu 1: 

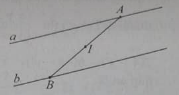
Hình có hai đường thẳng a và b song song với nhau thì có bao nhiêu phép đối xứng tâm biến a thành b?

A. Một      

B. Hai

C. Ba      

D. Vô số

Đáp án: D

Lấy hai điểm A, B bất kì lần lượt thuộc a, b. Trung điểm I của AB chính là tâm đối xứng của hình. Có vô số điểm I thỏa mãn. Chọn đáp án D

Câu 2: 

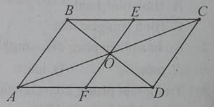
Cho hình bình hành ABCD tâm O. Gọi E, F lần lượt là trung điểm của các cạnh BC và AD. Phép đối xứng tâm O biến.

A. vecto DF thành vecto EB     

B. vecto EC thành vecto AF

C. vecto BO thành vecto OD       

D. vecto BE thành vecto DF

Đáp án: D

Chọn đáp án D

Nhận xét: ba phương án A, B, C đều sai về hướng của vecto

Câu 3: 

Trong mặt phẳng Oxy cho điểm M(-3;7). Phép đối xứng tâm O biến M thành M’ thì tọa độ M’ là:

A. M’(-3;-7)      

B. M’(3;-7)

C. M’(7;-3)      

D. M’(7;3)

Đáp án: B

Phép đối xứng tâm O biến M(x;y) thành M’(-x;-y). Chọn đáp án B

Câu 4: 

Trong mặt phẳng Oxy cho điểm M(2;-6) và điểm I(1;4). Phép đối xứng tâm I biến M thành M’ thì tọa độ M’ là:

A. M’(0;14)      

B. M’(14;0)

C. M’(-3/2;-2)      

D. M’(-1/2;5)

Đáp án: A

Phép đối xứng tâm I(x0; y0) biến M(x; y) thành M'(x'; y') thì:

⇒ M'(0;14). Chọn đáp án A

Câu 5: 

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 6y + 5 = 0 điểm I(2;-4). Phép đối xứng tâm I biến d thành d’ có phương trình:

A. 2x - 6y - 5 = 0

B. 2x - 6y - 61 = 0

C. 6x - 2y + 5 = 0

D. 6x - 2y + 61 = 0

Đáp án: B

Lấy M(x;y) thuộc d, phép đối xứng tâm I (x0; y0) biến M(x; y) thành M'(x'; y') thì

Thay vào phương trình d ta được :2(4 - x') - 6(-8 - y') + 5 = 0 ⇒ 2x' - 6y' - 61 = 0 hay 2x - 6y - 61 = 0. Chọn đáp án B

Câu 6: 

Hình nào dưới đây vừa có tâm đối xứng vừa có trục đối xứng?

A. hình bình hành      

B. hình chữ nhật

C. hình tam giác đều      

D. hình tam giác cân

Đáp án: B

Hình bình hành có tâm đối xứng; hình tam giác cân và hình tam giác đều chỉ có trục đối xứng.

Câu 7: 

Có bao nhiêu phép đối xứng tâm biến hình chữ nhật thành chính nó?

A. một      

B. hai

C. ba      

D. không

Đáp án: A

Câu 8: 

Trong mặt phẳng Oxy cho điểm M(-5;9). Phép đối xứng tâm I(2; -6) biến M thành M’ thì tọa độ M’ là.

A. M'(9;-15)      

B. M'(9;-3)

C.M'(9;-21)      

D. M'(1;-3)

Đáp án: C

Thử vào công thức : Phép đối xứng tâm I(x0;y0) biến M(x; y) thành M’(x’, y’) thì

Nhận xét: bài toán đơn giản nhưng rất dễ nhầm lẫn công thức tọa độ trung điểm của đoạn thẳng sang tọa độ vecto (lấy tọa độ điểm đầu trừ tạo độ điểm cuối, hoặc nhầm tọa độ trung điểm).

Câu 9: 

Trong mặt phẳng Oxy cho điểm I(2; -5). Phép đối xứng tâm I biến M(x; y) thành M'(3; 7). Tọa độ của M là:

A. M(5/2;1)      

B. M(7;-3)

C. M(-1;-12)      

D. M(1;-17)

Đáp án: D

Phép đối xứng tâm I(x0;y0) biến M(x; y) thành M’(x’, y’) thì:

Câu 10: 

Trong mặt phẳng Oxy phép đối xứng tâm I biến M(6; -9) thành M'(3;7). Tọa độ của tâm đối xứng I là:

A. I(-3/2; -8)      

B. (-3;16)

C. (9/2; -1)      

D. I(-3/2; -1)

Đáp án: C

Qua phép đối xứng tâm I biến M thành M’ nên I là trung điểm của MM’.

Tọa độ I bằng trung bình cộng tọa độ của M và M’.

Câu 11: 

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 6x + 5y - 7 = 0; điểm I(2;-1). Phép đối xứng tâm I biến d thành d’ có phương trình:

A. 6x - 5y - 7 = 0      

B. 6x + 5y - 7 = 0

C. 6x - 5y + 7 = 0      

D. 6x + 5y + 7 = 0

Đáp án: B

Tâm đối xứng I thuộc d thì phép đối xứng tâm I biến d thành chính nó.

Nhận xét: lưu ý kiểm tra xem tâm có thuộc d không, cũng như với phép tịnh tiến thì kiểm tra xem vecto tịnh tiến có cùng phương với vecto chỉ phương của d không.

Câu 12: 

Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình : 3x - 5y + 7 = 0; đường thẳng d’ có phương trình 3x - 5y + 12 = 0. Một lần đối xứng của (H) là:

A. (1;2)      

B. (-4;0)      

C. (0;19/2)      

D. (19/2;0)

Đáp án: C

Hai đường thẳng d và d’ song song. Điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên bị loại

Tính khoảng cách từ C tới hai đường thẳng d, d’

⇒ d(C;d)=d(C;d^')=> C là tâm đối xứng

Nhận xét: nếu I là tâm đối xứng của hình gồm hai đường thẳng song song thì I cách đều hai đường thẳng song song đó.

Câu 13: 

Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình 3x - 5y + 7 = 0 và đường thẳng d’ có phưng trình:

Tâm đối xứng của (H) là:

A. I(-7/2;7/2)      

B. I(7;-7)

C. I(7/2;7/2)      

D. I(7;7)

Đáp án: C

Đường thẳng d có vecto chỉ phương u→(5;3); Đường thẳng d’ có vecto chỉ phương v→(-3;1) nên d không song song với d’. Tâm đối xứng của hình (H) chính là giao điểm của d và d’:

Gọi I là giao điểm của d và d’.

Điểm I thuộc d’ nên tọa độ I(2- 3t; 4+ t)

Lại có, I thuộc d nên thay tọa độ điểm I vào phương trình đường thẳng d ta được:

3(2 - 3t) - 5(4 + t) + 7 = 0 ⇒ -14t = 7

Câu 14: 

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 2)2 + (y + 4)2 = 9 và đường tròn (C’) có phương trình (x - 3)2 + (y + 3)2 = 9. Phép đối xứng tâm K biến (C) thành (C’), tọa độ của K là:

A. K(2; -4)      

B. K(3; -3)

C. K(-7/2;5/2)      

D. K(5/2; -7/2)

Đáp án: D

Đường tròn (C) có tâm I(2; -4), bán kính R= 3

Đường tròn (C’) có tâm J( 3; -3) và bán kính R’ = 3

Vì R= R’ nên tồn tại phép đối xứng tâm: biến đường tròn (C) thành (C’).

Khi đó; tâm đối xứng K là trung điểm IJ.

Câu 15: 

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x2 + y2 + 2x - 6y + 6 = 0; điểm I(1;2). Phép đối xứng tâm I biến (C) thành (C’) có phương trình:

A. x2 + y2 - 6x - 2y + 6 = 0

B. x2 + y2 - 2x - 6y + 6 = 0

C. x2 + y2 + 6x - 2y - 6 = 0

D. x2 + y2 - 6x + 2y + 6 = 0

Đáp án: A

Phép đối xứng tâm I(1; 2) biến M(x; y) thành M’(x’; y’) thì:

Thay vào phương trình (C) ta được:

(2 - x' )2 + (4 - y')2 + 2(2 - x' ) - 6(4 - y' ) + 6 = 0

⇒ x'2 + y'2 - 6x' - 2y' + 6 = 0 hay x2 + y2 - 6x - 2y + 6 - 0

Câu 16: 

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình:

(x - 3)2 + (y - 1)2 = 4. Phép đối xứng có tâm O là gốc tọa độ biến (C) thành (C’) có phương trình:

A. x2 + y2 - 6x - 2y - 6 = 0

B. x2 + y2 - 2x - 6y + 6 = 0

C. x2 + y2 + 6x - 2y - 6 = 0

D. x2 + y2 + 6x + 2y + 6 = 0

Đáp án: D

Đường tròn (C) có tâm I(3; 1) và bán kính R = 2.

Phép đối xứng tâm O(0; 0) biến tâm I(3; 1) của (C) thành tâm I’(-3; -1) của đường tròn (C’), bán kính R = 2 không đổi.

Phương trình (C’) là (x + 3)2 + (y + 1)2 = 4 hay x2 + y2 + 6x + 2y + 6 = 0

Câu 17: 

Trong mặt phẳng Oxy cho parabol (P) có phương trình y = x2 - 3x + 1. Phép đối xứng tâm O(0;0) biến (P) thành (P’) có phương trình:

A. y = x2 + 3x - 1

B. y = -x2 + 3x + 1

C. y = -x2 - 3x - 1

D. y = -x2 - 3x + 1

Đáp án: C

Phép đối xứng tâm O biến M(x; y) thuộc (P) thành điểm M’(x’; y’) thuộc (P’).

Trong đó;

thay vào phương trình (P) ta được

hay y = -x2 - 3x - 1

Câu 18: 

Trong mặt phẳng Oxy cho parabol (P) có phương trình: y = x2 - 3x + 1. Phép đối xứng tâm I(4; -3) biến P thành (P’) có phương trình:

A. y = -x2 + 13x - 47

B. y = x2 - 13x + 47

C. y = -x2 - 13x - 47

D. y = -x2 - 13x + 47

Đáp án: A

Phép đối xứng tâm I biến M(x; y) thành M’(x’; y’) thì:

Thay vào phương trình (P) ta được:

-6 - y' = (8 - x')2 - 3(8 - x') + 1 ⇒ -y' = x'2 - 13x' + 47 hay y = -x2 + 13x - 47

Câu 19: 

Trong mặt phẳng Oxy cho đường thẳng d có phương trình x - 2y + 20 = 0; đường thẳng d’ có phương trình x - 2y - 8 = 0. Tìm tọa độ điểm I sao cho phép đối xứng tâm I biến d thành d’ đồng thời biến trục Oy thành chính nó.

A. I(-2;0)      

B. I(8;0)

C. I(-3/2;0)      

D. I(0; -3/2)

Đáp án: D

Dễ thấy d // d’, ta có d ∩ Oy = A(0; 1); d’ ∩ Oy = A’(0; -4). Phép đối xứng tâm I biến Oy thành Oy thì I thuộc trục Oy; biến d thành d’ thì I là trung điểm của AA’ ⇒ I(0; -3/2).

Câu 20: 

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình:

(x - 3)2 + (y - 1)2 = 4. Phép đối xứng có tâm O là gốc tọa độ biến (C) thành (C’) có phương trình:

A. x2 + y2 - 6x - 2y - 6 = 0

B. x2 + y2 - 2x - 6y + 6 = 0

C. x2 + y2 + 6x - 2y - 6 = 0

D. x2 + y2 + 6x + 2y + 6 = 0

Đáp án: D

Đường tròn (C) có tâm I(3; 1) và bán kính R = 2.

Phép đối xứng tâm O(0; 0) biến tâm I(3; 1) của (C) thành tâm I’(-3; -1) của đường tròn (C’), bán kính R = 2 không đổi.

Phương trình (C’) là (x + 3)2 + (y + 1)2 = 4 hay x2 + y2 + 6x + 2y + 6 = 0

CLICK NGAY vào TẢI VỀ dưới đây để download hướng dẫn bộ 20 câu hỏi trắc nghiệm Toán hình 11 Phép đối xứng tâm file word, pdf hoàn toàn miễn phí.