3. C2-7c+6=c-frac C-1 - Gauthmath

Trang chủ » C2-7c+6=(c-__)(c-1) » 3. C2-7c+6=c-frac C-1 - Gauthmath

Có thể bạn quan tâm

Math Resources/Physics/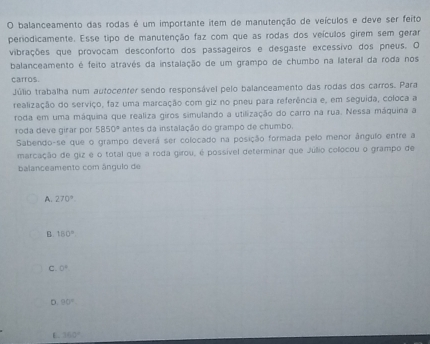

Question

balanceamento das rodas é um importante item de manutenção de veículos e deve ser feito periodicamente. Esse tipo de manutenção faz com que as rodas dos veículos girem sem gerar vibrações que provocam desconforto dos passageiros e desgaste excessivo dos pneus. O balanceamento é feito através da instalação de um grampo de chumbo na lateral da roda nos carros. Júlio trabalha num autocenter sendo responsável pelo balanceamento das rodas dos carros. Para realização do serviço, faz uma marcação com giz no pneu para referência e, em seguida, coloca a roda em uma máquina que realiza giros simulando a utilização do carro na rua. Nessa máquina a roda deve girar por 5850° antes da instalação do grampo de chumbo. Sabendo-se que o grampo deverá ser colocado na posição formada pelo menor ângulo entre a marcação de giz é o total que a roda girou, é possível determinar que Júllio collocou o grampo de balanceamento com ângulo de A. 270° B. 150° C. 0° D 90° E. 360°SHOW LESS0

Solution

Responder: E. $$360^{\circ }$$

Para determinar o ângulo em que Júlio colocou o grampo de balanceamento, precisamos subtrair o ângulo formado pela marcação de giz do ângulo total que a roda girou.

Ângulo do grampo de balanceamento = Ângulo total - Ângulo da marcação de giz

Ângulo do grampo de balanceamento = $$5850^{\circ } - 360^{\circ }$$

Ângulo do grampo de balanceamento = $$5490^{\circ }$$

Portanto, Júlio colocou o grampo de balanceamento com um ângulo de $$5490^{\circ }$$.

Click to rate:25.0(48 votes)Search questionBy textBy image/screenshotDrop your file here orClick Hereto upload

Từ khóa » C2-7c+6=(c-__)(c-1)