§3. Các Phép Toán Tập Hợp - Hoc24
Có thể bạn quan tâm
I. GIAO CỦA HAI TẬP HỢP
Tập hợp \(C\) gồm các phần tử vừa thuộc tập hợp \(A\), vừa thuộc tập hợp \(B\) được gọi là giao của \(A\) và \(B\).
Kí hiệu \(C=A\cap B\)
Vậy \(A\cap B=\left\{x|x\in A;x\in B\right\}\)
\(x\in A\cap B\Leftrightarrow\left\{{}\begin{matrix}x\in A\\x\in B\end{matrix}\right.\)
Tập hợp \(A\cap B\) được biểu diễn bởi phần gạch chéo trong biểu đồ Ven sau:
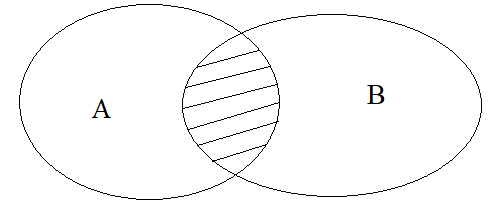
Ví dụ 1: Xét các tập hợp:
\(A=\) {\(n\in N\)\(|n\) là ước của 12} ;
\(B=\) {\(n\in N\)\(|n\) là ước của 18};
\(C=\) {\(n\in N\)\(|n\) là ước chung của 12 và 18}.
Ta có thể liệt kê phần tử của 3 tập hợp trên như sau:
\(A=\left\{1,2,3,4,6,12\right\}\)
\(B=\left\{1,2,3,6,9,18\right\}\)
\(C=\left\{1,2,3,6\right\}\)
Ta thấy các phần tử của \(C\) đều là phần tử của \(A\) và của \(B\). Do đó \(C=A\cap B\).
@70221@II. HỢP CỦA HAI TẬP HỢP
Tập hợp \(C\) gồm các phần tử thuộc tập hợp \(A\) hoặc thuộc tập hợp \(B\) được gọi là hợp của \(A\) và \(B\).
Kí hiệu \(C=A\cup B\)
Như vậy \(A\cup B=\) {\(x|x\in A\) hoặc \(x\in B\)}
\(x\in A\cup B\Leftrightarrow\left[{}\begin{matrix}x\in A\\x\in B\end{matrix}\right.\)
Tập hợp \(A\cup B\) còn được biểu diễn bởi phần gạch chéo trên biểu đồ Ven sau:
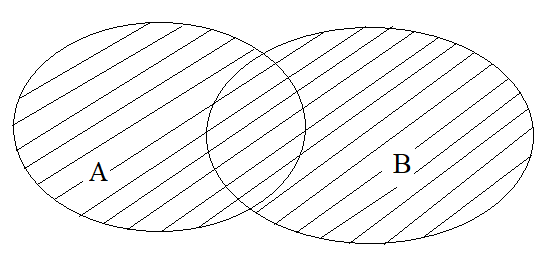
Ví dụ 2: Xét tập hợp \(A=\left\{1,3,5,7,9\right\}\)
và tập hợp \(B=\left\{2,4,6,8,10\right\}\)
Khi đó \(C=A\cup B=\left\{1,2,3,4,5,6,7,8,9,10\right\}\)
Ví dụ 3: Giả sử \(A\), \(B\) lần lượt là tập hợp các học sinh giỏi Toán và giỏi Văn của lớp 10E. Biết: \(A=\) {Minh, Nam, Lan, Hồng, Nguyệt}
và \(B=\) {Cường, Lan, Dũng, Hồng, Tuyết, Lê}.
(các học sinh trong lớp không trùng tên nhau)
Gọi \(C\) là tập hợp đội tuyển thi học sinh giỏi của lớp bao gồm các học sinh giỏi Toán hoặc giỏi Văn.
Ta có thể viết tập hợp \(C\) bằng cách liệt kê các phần tử như sau:
\(C=\) {Minh, Nam, Lan, Hồng, Nguyệt, Cường, Dũng, Tuyết, Lê}
Ta nói rằng \(C\) là hợp của \(A\) và \(B\).
@21486@III. HIỆU VÀ PHẦN BÙ CỦA HAI TẬP HỢP
Tập hợp \(C\) gồm các phần tử thuộc \(A\) nhưng không thuộc \(B\) được gọi là hiệu của \(A\) và \(B\).
Kí hiệu: \(C=A\)\\(B\)
Vậy \(A\)\\(B\)\(=\left\{x|x\in A;x\notin B\right\}\)
\(x\in\) \(A\)\\(B\) \(\Leftrightarrow\left[{}\begin{matrix}x\in A\\x\notin B\end{matrix}\right.\)
Tập hợp \(A\)\\(B\) còn được biểu diễn bởi phần gạch chéo trên biểu đồ Ven sau:

Ví dụ 4: Xét 2 tập hợp:
\(A=\left\{x\in N|x< 10,x⋮2\right\}\)
\(B=\left\{x\in N|x< 10,x⋮4\right\}\)
Liệt kê các phần tử của tập hợp \(A\)\\(B\) .
Giải:
Ta có thể liệt kê các phần tử của các tập hợp trên như sau:
\(A=\left\{0,2,4,6,8\right\}\)
\(B=\left\{0,4,8\right\}\)
Như vậy \(A\)\\(B\) \(=\left\{2,6\right\}\).
Khi \(B\subset A\) thì \(A\)\\(B\) gọi là phần bù của \(B\) trong \(A\), kí hiệu là \(C_AB\).
(Phần gạch chéo trong biểu đồ Ven dưới đây)
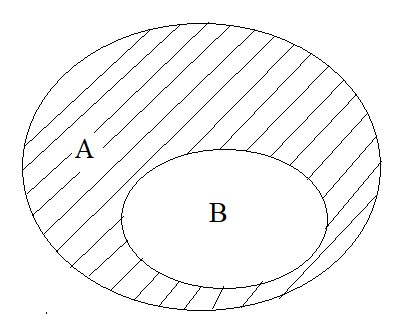
Từ khóa » Các Phép Toán Tập Hợp
-
Lý Thuyết Toán 10 Các Phép Toán Tập Hợp - Marathon Education
-
Các Phép Toán Tập Hợp - Toán 10
-
Lý Thuyết Các Phép Toán Trên Tập Hợp Môn Toán Lớp 10
-
Giải Bài Tập Toán 10 Bài 3: Các Phép Toán Tập Hợp (sách Mới)
-
Toán 10 Bài 3: Các Phép Toán Tập Hợp - Lý Thuyết - Hoc247
-
Giải Bài 3: Các Phép Toán Tập Hợp | Đại Số 10 Trang 13 - 15 - Tech12h
-
Soạn đại Số 10 Bài 3: Các Phép Toán Tập Hợp | Học Cùng
-
Toán 10 Bài 3: Các Phép Toán Tập Hợp
-
Các Phép Toán Trên Tập Hợp: Lý Thuyết, Ví Dụ Và Bài Tập
-
Tập Hợp Và Các Phép Toán Trên Tập Hợp, Trắc Nghiệm Toán Học Lớp 10
-
Lý Thuyết Về Các Phép Môn Toán Tập Hợp
-
Các Phép Toán Tập Hợp - Bài 3 - Thầy Lê Thành Đạt (DỄ HIỂU NHẤT)
-
Tập Hợp Và Các Phép Toán Trong Tập Hợp - Thầy Nguyễn Công Chính