3. Chuyển động Thẳng Biến đổi đều - Củng Cố Kiến Thức
Có thể bạn quan tâm
I. VẬN TỐC TỨC THỜI. CHUYỂN ĐỘNG THẲNG ĐỀU
1. Độ lớn của vận tốc tức thời
Đại lượng: $v = \frac{{\Delta s}}{{\Delta t}}$
là độ lớn của vận tốc tức thời của xe tại $M.$ Nó cho ta biết tại M xe chuyển động nhanh hay chậm.
Trên một xe máy đang chạy thì đồng hồ tốc độ (còn gọi là tốc kế) trước mặt người lái xe chỉ độ lớn của vận tốc tức thời của xe.

2. Vectơ vận tốc tức thời
Đại lượng: $v = \frac{{\Delta s}}{{\Delta t}}$
Vectơ vận tốc tức thời của một vật tại một điểm là một vectơ có gốc tại vật chuyển động, có hướng của chuyển động và có độ dài tỉ lê với độ lớn của vận tốc tức thời theo một tỉ xích nào đó.
3. Chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi là chuyển động có quỹ đạo là đường thẳng và có độ lớn của vận tốc tức thời luôn biến đổi.
Loại chuyển động thẳng biến đổi đơn giản nhất là chuyển động thẳng biến đổi đều. Trong chuyển động thẳng biến đổi đều, độ lớn của vận tốc tức thời hoặc tăng đều, hoặc giảm đều theo thời gian.
Chuyển động thẳng có độ lớn của vận tốc tức thời tăng đều theo thời gian gọi là chuyển động thẳng nhanh dần đều.
Chuyển động thẳng có độ lớn của vận tốc tức thời giảm đều theo thời gian gọi là chuyển động thẳng chậm dần đều.
Khi nói vận tốc của vật tại vị trí hoặc thời điểm nào đó, ta hiểu đó là vận tốc tức thời.
II. CHUYỂN ĐỘNG THẲNG NHANH DẦN ĐỀU
1. Gia tốc trong chuyển động thẳng nhanh dần đều
a) Khái niệm gia tốc
Hệ số tỉ lệ a là một đại lượng không đổi và gọi là gia tốc của chuyển động. Gia tốc a bằng thương số:
$a = \frac{{\Delta v}}{{\Delta t}}$
Gia tốc của chuyển động là đại lượng xác định bằng thương số giữa độ biến thiên vận tốc $\Delta v$ và khoảng thời gian vận tốc biến thiên $\Delta t.$
b) Vectơ gia tốc
Vì vận tốc là đại lượng vectơ nên gia tốc cũng là đại lượng vectơ:
$\overrightarrow a = \frac{{\overrightarrow v - \overrightarrow {{v_o}} }}{{t - {t_o}}} = \frac{{\Delta \overrightarrow v }}{{\Delta t}}$
Khi vật chuyển động thẳng nhanh dần đều, vectơ gia tốc có gốc ở vật chuyển động, có phương và chiều trùng với phương và chiều của vectơ vận tốc và có độ dài tỉ lệ với độ lớn của gia tốc theo một tỉ xích nào đó.
2. Vận tốc của chuyển động thẳng nhanh dần đều
a) Công thức tính vận tốc
$v = {v_o} + at$
Đây là công thức tính vận tốc. Nó cho ta biết vận tốc của vật ở những thời điểm khác nhau.
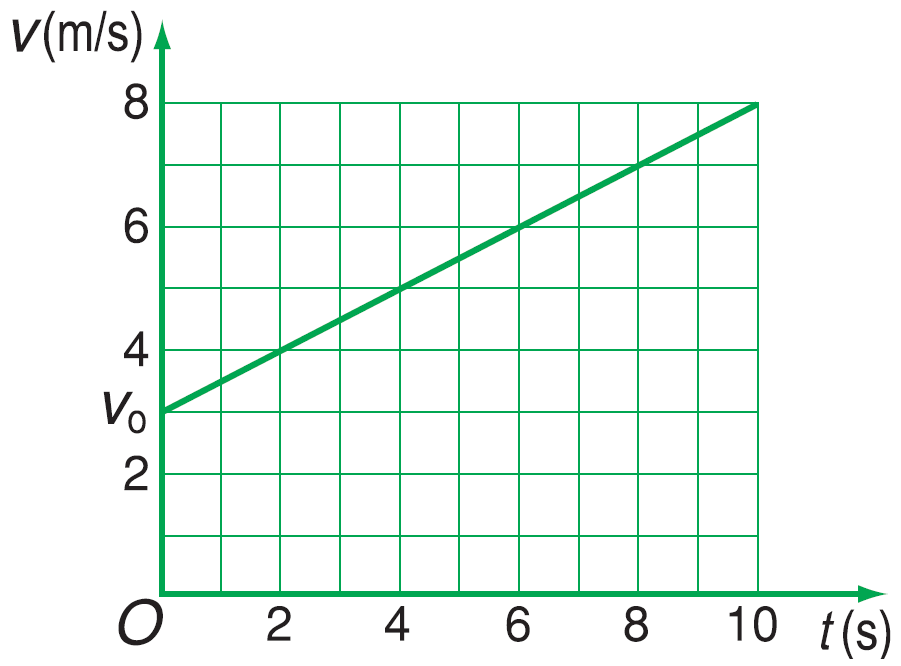
b) Đồ thị vận tốc – thời gian
Đồ thị biểu diễn sự biến thiên của vận tốc tức thời theo thời gian gọi là đồ thị vân tốc - thời gian. Đó là đổ thị ứng với công thức $v = {v_o} + at$, trong đó $v$ coi như một hàm số của thời gian $t$. Đồ thị có dạng một đoạn thẳng như sau:
3. Công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều
Tốc độ trung bình của chuyển động là:
${v_{tb}} = \frac{s}{t}$
Công thức tính quãng đường đi được của chuyển động thẳng nhanh dần đều là:
$s = {v_o}t + \frac{1}{2}a{t^2}$
Công thức này cho thấy quãng đường đi được trong chuyển động thẳng nhanh dần đều là một hàm số bậc hai của thời gian.
4. Công thức liên hệ giữa gia tốc, vận tốc và quãng đường đi được của chuyển động thẳng nhanh dần đều
${v^2} - v_o^2 = 2as$
5. Phương trình chuyển động của chuyển động thẳng nhanh dần đều
$x = {x_o} + {v_o}t + \frac{1}{2}a{t^2}$
III. CHUYỂN ĐỘNG THẲNG CHẬM DẦN ĐỀU
1. Gia tốc của chuyển động thẳng chậm dần đều
a) Công thức tính gia tốc
$a = \frac{{\Delta v}}{{\Delta t}} = \frac{{v - {v_o}}}{{t - {t_o}}}$
b) Vectơ gia tốc
$\overrightarrow a = \frac{{\Delta \overrightarrow v }}{{\Delta t}}$
Vectơ gia tốc của chuyển động thẳng chậm dần đều ngược chiều với vectơ vận tốc.
2. Vận tốc của chuyển động thẳng chậm dần đều
a) Công thức tính vận tốc
$v = {v_o} + at$
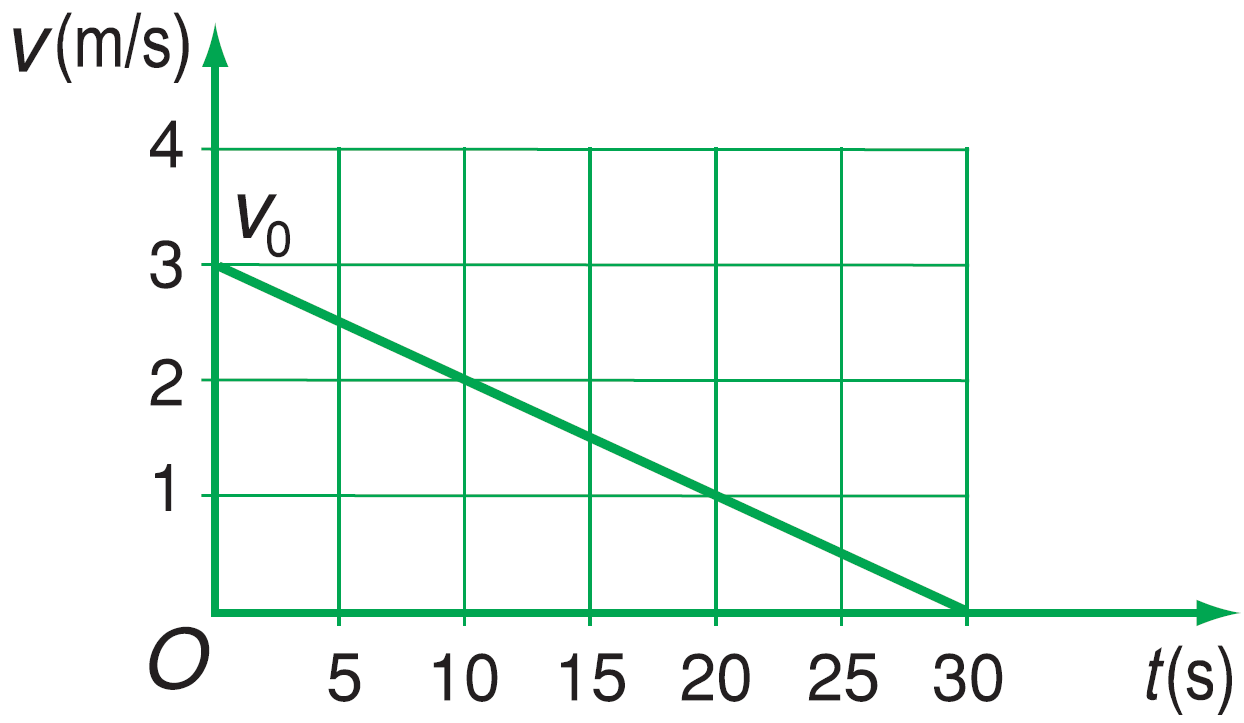
b) Đồ thị vận tốc – thời gian có dạng như hình sau:
3. Công thức tính quãng đường đi được và phương trình chuyển động của chuyển động thẳng chậm dần đều
a) Công thức tính quãng đường đi được
$s = {v_o}t + \frac{1}{2}a{t^2}$
b) Phương trình chuyển động của chuyển động thẳng chậm dần đều
$x = {x_o} + {v_o}t + \frac{1}{2}a{t^2}$
Từ khóa » Gia Tốc Trong Cđ Thẳng Nhanh Dần đều
-
Gia Tốc Của Chuyển động Thẳng Nhanh Dần đều
-
Gia Tốc Của Chuyển động Thẳng Nhanh, Chậm Dần đều Có đặc điểm ...
-
Gia Tốc Của Chuyển động Thẳng Nhanh Dần đều Có Phương, Chiều ...
-
Gia Tốc Của Chuyển động Thẳng Nhanh Dần đều: - Hoc247
-
Tổng Hợp Các Lý Thuyết Và Công Thức Lý 10 Cơ Bản Quan Trọng
-
Lý Thuyết Chuyển động Thẳng Biến đổi đều | SGK Vật Lí Lớp 10
-
Trong Chuyển động Thẳng Nhanh Dần đều Gia Tốc Có Luôn Dương ...
-
Công Thức Gia Tốc Của Chuyển động Thẳng Biến đổi đều.
-
Giáo án Chuyển động Thẳng đều (tiếp) - Thư Viện Đề Thi
-
Giải Bài Tập Vật Lí 10 - Bài 3: Chuyển động Thẳng Biến đổi đều
-
Hãy Nêu đầy đủ Các Tính Chất đặc Trưng Cho Chuyển động Thẳng Nhan
-
Chuyển động Thẳng – Wikipedia Tiếng Việt
-
Chuyển động Thẳng Biến đổi đều Ôn Tập Vật Lí 10
-
Chuyển độn Thẳng Nhanh Dần đều, Chậm Dần đều Là Gì?