30 Đề Thi Học Kì 1 Toán 7 Có đáp án Năm 2020 - 2021

13 Đề thi học kì 1 Toán 7 Chân trời sáng tạo năm học 2024 - 2025Bộ đề thi học kì 1 lớp 7 môn Toán có đáp ánBài trướcTải vềBài sauNâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi. Mua ngay Từ 79.000đ Tìm hiểu thêm

Đề thi học kì 1 Toán 7 Có đáp án

• 1. Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo - Đề 1
  • Đề thi
  • Đáp án
• 2. Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo Đề 2
  • Đề thi
  • Đáp án
• Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo - Đề 3
• Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo - Đề 4
• Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo - Đề 5

Bộ đề thi học kì 1 môn Toán lớp 7 Chân trời sáng tạo có đáp án được VnDoc tổng hợp và đăng tải gồm 13 đề thi sẽ là tài liệu hữu ích cho các em ôn tập, chuẩn bị cho kì thi học kì 1 lớp 7 sắp tới. Đây cũng là tài liệu hay cho thầy cô tham khảo ra đề và ôn luyện cho học sinh.

Lưu ý: Toàn bộ 13 đề thi và đáp án đều có trong file tải về. Mời các bạn tải về xem trọn bộ tài liệu

1. Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo - Đề 1

Đề thi

I. PHẦN TRẮC NGHIỆM: (3,0 điểm)

Khoanh vào chữ cái đặt trước câu trả lời đúng.

Câu 1: Trong các câu sau, câu nào đúng?

A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương;

B. Số 0 là số hữu tỉ dương;

C. Số nguyên âm không phải là số hữu tỉ âm;

D. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm.

Câu 2: Phát biểu nào sau đây là sai?

A. Mọi số vô tỉ đều là số thực.

B. Mọi số thực đều là số vô tỉ.

C. Số 0 là số hữu tỉ.

D. \(- \sqrt 2\) là số vô tỉ.

Câu 3: Nhận xét đúng về căn bậc hai số học của 7 là:

A. một số hữu tỉ;

B. một số tự nhiên;

C. một số nguyên dương;

D. một số vô tỉ.

Câu 4: Trong các số sau, số nào là số vô tỉ?

A. 0,23;

B. 1,234567…;

C. 1,33333…;

D. 0,5.

Câu 5: Cho tam giác ABC. Qua đỉnh A vẽ đường thẳng a song song với BC, qua đỉnh B vẽ đường thẳng b song song với AC. Số đường thẳng a, b vẽ được lần lượt là:

A. 1; 1;

B. 0; 0;

C. 2; 1;

D. Vô số đường thẳng a và b.

Câu 6: Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Hình lăng trụ có chiều cao AA' = 3 cm. Thể tích của hình lăng trụ đó là:

A. V = 9 cm3;

B. V = 18 cm3;

C. V = 24 cm3;

D. V = 36 cm3.

Câu 7: Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau”. Hãy chỉ ra giả thiết và kết luận của định lí trên.

A. Giả thiết: “một đường thẳng cắt hai đường thẳng”; Kết luận: “song song thì hai góc đồng vị bằng nhau”;

B. Giả thiết: “một đường thẳng”; Kết luận: “cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau”;

C. Giả thiết: “một đường thẳng cắt hai đường thẳng song song”; Kết luận: “hai góc đồng vị bằng nhau”;

D. Giả thiết: “một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị”; Kết luận: “bằng nhau”.

Câu 8: Một hình hộp chữ nhật có chiều dài, chiều cao và diện tích xung quanh lần lượt là 8 m; 5 m và 100 m2. Chiều rộng của hình hộp chữ nhật là:

A. 3 m;

B. 2 m;

C. 4 m;

D. 1 m.

Câu 9: Biểu đồ dưới đây cho biết tỉ số phần trăm học sinh tham gia các môn thể thao của lớp 7A.

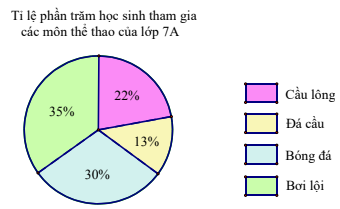
Căn cứ vào biểu đồ sau đây, hãy cho biết môn nào có các học sinh lớp 7A tham gia ít nhất?

A. Cầu lông

B. Bơi lội;

C. Bóng đá;

D. Đá cầu.

Câu 10: Cho biểu đồ sau:

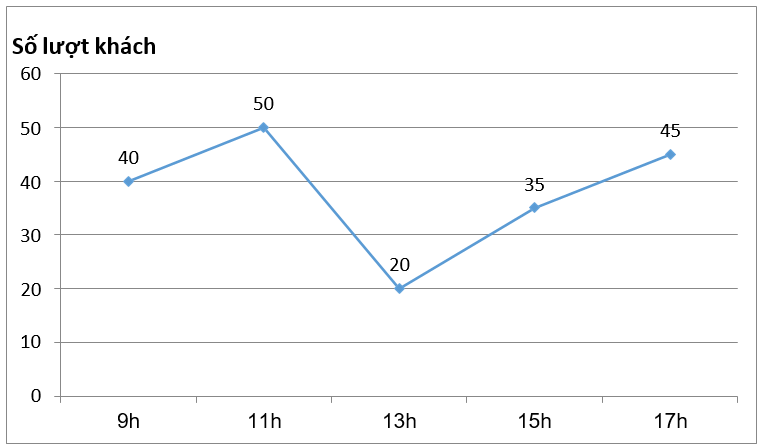
Các số trên mỗi đầu mút đoạn thẳng của hình trên thể hiện số khách hàng đến cửa hàng đó. Hỏi vào thời điểm nào có nhiều khách đến cửa hàng nhất?

A. 17h;

B. 9h;

C. 11h;

D. 13h.

II. PHẦN TỰ LUẬN (7,0 điểm)

Câu 1(2 điểm) Tìm x, biết:

a) \(\dfrac{1}{3}:x = 2\dfrac{2}{3}:\left( { - 0,3} \right)\)

b) \({3^{2x}} - {2.3^5} = {3^5}\)

c) \(2x - \sqrt {1,69} = \sqrt {1,21}\)

d) \(\left| {x + \dfrac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\)

Câu 2 (1đ): Tính diện tích xung quanh và thể tích hình lăng trụ đứng trong hình vẽ sau.

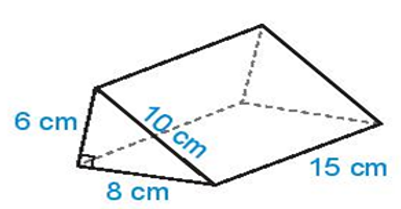
Câu 3 (1đ): Một cái thước thẳng có độ dài 23 inch, hãy tính độ dài của thước này theo đơn vị cm với độ chính xác d = 0,05 (cho biết 1 inch ≈ 2,54 cm).

Câu 4 (1đ): Cho biểu đồ hình quạt tròn dưới đây biểu diễn tỉ số phần trăm số size áo bán ra của một cửa hàng.

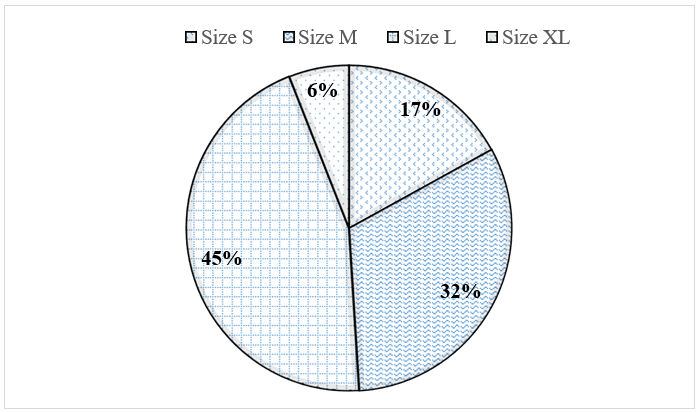
Quan sát biểu đồ, hãy cho biết:

a) Lượng size áo nào bán ra được nhiều nhất?

b) Size M bán được nhiều hơn size XL là bao nhiêu phần trăm?

Bài 6 (1đ):

Quan sát hình vẽ bên dưới:

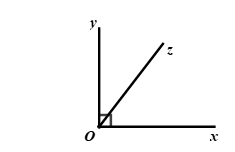
Tính số đo góc xOz, biết \(\dfrac{1}{5}\angle xOz = \dfrac{1}{4}\angle yOz\).

Câu 7 (1đ): Bác Nga gửi tiền tiết kiệm có kỳ hạn 12 tháng với số tiền 20 000 000 đồng, lĩnh lãi cuối kỳ tại Ngân hàng BIDV, lãi suất 6,4%/năm. Hỏi số tiền cả gốc lẫn lãi bác Nga thu được sau khi gửi 15 tháng là bao nhiêu?

Đáp án

I. Bảng đáp án trắc nghiệm

1. A	2. B	3. D	4. B	5. A
6. B	7. C	8. B	9. D	10. C

II. PHẦN TỰ LUẬN (7,0 điểm)

Câu 1 (2đ)

a) \(\dfrac{1}{3}:x = 2\dfrac{2}{3}:\left( { - 0,3} \right)\)

\(\begin{array}{l}\dfrac{1}{3}:x = \dfrac{8}{3}:\dfrac{{ - 3}}{{10}}\\\dfrac{1}{3}:x = \dfrac{8}{3}.\dfrac{{10}}{{ - 3}}\\\dfrac{1}{3}:x = \dfrac{{80}}{{ - 9}}\\x = \dfrac{1}{3}:\dfrac{{80}}{{ - 9}} = \dfrac{1}{3}.\dfrac{{ - 9}}{{80}}\\x = \dfrac{{ - 3}}{{80}}\end{array}\)

Vậy \(x = \dfrac{{ - 3}}{{80}}\)

b) \({3^{2x}} - {2.3^5} = {3^5}\)

\(\begin{array}{l}{3^{2x}} = {3^5} + {2.3^5}\\{3^{2x}} = \left( {1 + 2} \right){.3^5}\\{3^{2x}} = {3.3^5} = {3^1}{.3^5}\\{3^{2x}} = {3^{1 + 5}}\\{3^{2x}} = {3^6}\\ \Rightarrow 2x = 6\\\,\,\,\,\,\,\,\,\,\,x = 6:2\\\,\,\,\,\,\,\,\,\,\,x = 3\end{array}\)

Vậy x = 3

c) \(2x - \sqrt {1,69} = \sqrt {1,21}\)

\(\begin{array}{l}2x - 1,3 = 1,1\\2x = 1,1 + 1,3\\2x = 2,4\\x = 2,4:2\\x = 1,2\end{array}\)

Vậy x = 1,2

d) \(\left| {x + \dfrac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\)

Trường hợp 1:

\(\begin{array}{l}\left| {x + \dfrac{1}{3}} \right| = 0\\x + \dfrac{1}{3} = 0\\x = \dfrac{{ - 1}}{3}\end{array}\)

Trường hợp 2: \({x^2} + 1 = 0\)

Vì \({x^2} \ge 0\) với mọi x nên \({x^2} + 1 \ge 1 > 0\) với mọi x

Do đó, không có x thỏa mãn \({x^2} + 1 = 0\)

Vậy \(x = - \dfrac{1}{3}\)

Câu 2 (1đ):

Diện tích xung quanh của hình lăng trụ đứng là:

(6 + 8 + 10) . 15 = 360 (cm2)

Thể tích hình lăng trụ đứng là:

\(\frac{1}{2}\)  .  6  .  8  .  15 = 360 (cm3)

Vậy hình lăng trụ đứng có diện tích xung quanh là 360 cm2 và thể tích là 360 cm3.

Câu 3 (1đ):

Ta có: 1 inch ≈ 2,54 cm.

Khi đó, thước thẳng có độ dài 23 inch tính theo đơn vị cm là:

23 . 2,54 = 58,42 (cm)

Vì độ chính xác đến hàng phần trăm nên ta làm tròn số 58,42 đến hàng phần mười. Khi đó: 58,42 ≈ 58,4.

Vậy độ dài của cái thước xấp xỉ 58,4 cm.

Câu 4 (1đ):

Quan sát biểu đồ, ta thấy:

Lượng size áo bán ra của một của hàng như sau:

- Size S chiếm 17%;

- Size M chiếm 32%;

- Size L chiếm 45%;

- Size XL chiếm 6%.

a) Ta thấy: 45% > 32% > 17% > 6%.

Do đó lượng size L bán ra được nhiều nhất.

b) Size M bán được nhiều hơn size XL là:

32% − 6% = 26%

Vậy size M bán được nhiều hơn size XL là 26%.

Câu 5

Ta có: \(\dfrac{1}{5}\angle xOz = \dfrac{1}{4}\angle yOz\) suy ra \(\angle yOz = \dfrac{4}{5}\angle xOz\)

Vì hai góc xOz và yOz là hai góc kề nhau nên\(\angle xOy = \angle xOz + \angle yOz = {90^0}\)

\(\begin{array}{l} \Rightarrow \angle xOz + \dfrac{4}{5}\angle xOz = {90^0}\\ \Rightarrow \left( {1 + \dfrac{4}{5}} \right).\angle xOz = {90^0}\\ \Rightarrow \dfrac{9}{5}.\angle xOz = {90^0}\\ \Rightarrow \angle xOz = {90^0}:\dfrac{9}{5} = {90^0}.\dfrac{5}{9}\\ \Rightarrow \angle xOz = {50^0}\end{array}\)

Vậy \(\angle xOz = {50^0}\)

Câu 6 (1đ):

Số tiền lãi bác Nga thu được sau 15 tháng gửi tiền tiết kiệm là:

20  000  000  .  6,4%  .  \(\frac{15}{12}\) =160  000 (đồng).

Số tiền cả gốc lẫn lãi bác Nga thu được sau 15 tháng gửi tiền tiết kiệm là:

20 000 000 + 160 000 = 20 160 000 (đồng).

Vậy số tiền cả gốc lẫn lãi bác Nga thu được sau 15 tháng gửi tiền tiết kiệm là 20 160 000 đồng.

2. Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo Đề 2

Đề thi

I. PHẦN TRẮC NGHIỆM: (3,0 điểm)

Khoanh vào chữ cái đặt trước câu trả lời đúng.

Câu 1: Trong các câu sau, câu nào sai?

A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương

B. Số tư nhiên hớn hơn số hữu tỉ âm

C. Số nguyên âm không phải là số hữu tỉ

D. Số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm

Câu 2: Số đối của số hữu tỉ \(\frac{-1}{12}\) là

A. 12;

B. \(-\frac{1}{12}\);

C. \(\frac{1}{12}\);

D. −12.

Câu 3: Căn bậc hai số học của 25 là

A. −5;

B. ±5;

C. \(-\sqrt{25}\);

D. 5.

Câu 4: Số \(\sqrt{3}\) thuộc tập hợp số nào sau đây?

A. ℤ;

B. 𝕀;

C. ℚ;

D. ℕ.

Câu 5: Cho điểm M nằm ngoài đường thẳng d. Có bao nhiêu đường thẳng qua M và song song với d?

A. 0;

B. 1;

C. 2;

D. vô số.

Câu 6: Cho lăng trụ đứng có kích thước như hình vẽ.

Số nào trong các số sau đây là diện tích xung quanh của hình lăng trụ đứng đó?

A. 120 cm2;

B. 24 cm2;

C. 128 cm2;

D. 200 cm2.

Câu 7: Một hình lăng trụ đứng tứ giác có độ dài cạnh bên là 20cm và đáy là hình thoi với độ dài hai đường chéo là 18cm;30cm. Tính thể tích của hình lăng trụ đó.

A.\(6\,300\,c{m^3}\)

B. \(5\,400\,c{m^3}\)

C. \(3\,600c{m^3}\)

D. \(4\,800\,c{m^3}\)

Câu 8: Trong các câu sau, câu nào cho một định lí?

A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia;

B. Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia;

C. Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song;

D. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.

Câu 9: Biểu đồ dưới đây cho biết tỉ số phần trăm diện tích trồng các loại cây ăn quả ở một trang trại.

Căn cứ vào biểu đồ sau đây, hãy cho biết tỉ số phần trăm diện tích trồng các loại cây ăn quả khác là bao nhiêu?

A. 27,5%;

B. 20%;

C. 17,5%;

D. 35%.

Câu 10: Cho biểu đồ sau:

Năm nào có tỉ lệ học sinh THCS nghiện điện thoại cao nhất?

A. 2021;

B. 2020;

C. 2019;

D. 2018.

Phần II. Tự luận (7 điểm):

Bài 1: (2,0 điểm)

Tính hợp lí (nếu có thể):

a)\(\dfrac{{ - 15}}{{14}}:\dfrac{{17}}{{23}} - \dfrac{{15}}{{14}}:\dfrac{{17}}{{11}} - \dfrac{6}{7}\)

b) \(\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2}} \right):\dfrac{{17}}{{13}} + \left( {\dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right):\dfrac{{17}}{{13}}\)

c) \({3^2}.\dfrac{1}{{243}}{.81^2}.\dfrac{1}{{{3^3}}}\)

d) \(\left( {{{4.2}^5}} \right):\left( {{2^3}.\dfrac{1}{{16}}} \right)\)

Bài 2: (2,0 điểm)

Tìm x, biết:

a) \(\left( { - 0,2} \right) - x.\dfrac{1}{6} = \dfrac{2}{3}\)

b) \(\left( {\dfrac{1}{3}x - \dfrac{8}{{13}}} \right).\left( {2,5 + \dfrac{{ - 7}}{5}:x} \right) = 0\)

c) \(5.\left( {\dfrac{1}{{\sqrt {25} }} - x} \right) - \sqrt {\dfrac{1}{{81}}} = \dfrac{{ - 1}}{9}\)

d) \(\left| x \right| - \dfrac{{23}}{{17}} = 0\)

Bài 3: (1,5 điểm)

Một chiếc khay nhựa đựng đồ có dạng hình hộp chữ nhật như hình vẽ bên dưới.

Dựa vào kích thước trên hình (coi mép khay nhựa không đáng kể), hãy tỉnh:

a) Diện tích xung quanh của chiếc khay.

b) Diện tích nhựa để làm chiếc khay trên.

c) Thể tích nước khay nhựa có thể chứa được.

Bài 4: (1,0 điểm)

Chi phí xây dựng nhà được biểu diễn qua biểu đồ hình quạt tròn sau:

a) Tính số phần trăm chi phí gạch. Biết rằng chi phí giám sát thi công, thép, gạch bằng nhau.

b) Biết rằng để xây dựng một ngôi nhà bác An đã chi trả hết 2,5 tỉ đồng. Hỏi chi phí trả tiền công là bao nhiêu?

Bài 5: (0,5 điểm)

Cho hai góc có cạnh tương ứng song song cùng nhọn hoặc cùng tù. Biết hai tia phân giác của chúng không cùng nằm trên một đường thẳng. Chứng minh rằng hai tia phân giác này song song với nhau.

Đáp án

Phần I: Trắc nghiệm

I. Bảng đáp án trắc nghiệm

1.C	2. C	3. B	4. B	5. B
6. C	7. A	8. A	9. D	10. A

Phần II. Tự luận:

Bài 1

Cách giải:

a) \(\dfrac{{ - 15}}{{14}}:\dfrac{{17}}{{23}} - \dfrac{{15}}{{14}}:\dfrac{{17}}{{11}} - \dfrac{6}{7}\)

\(\begin{array}{l} = \dfrac{{ - 15}}{{14}}.\dfrac{{23}}{{17}} - \dfrac{{15}}{{14}}.\dfrac{{11}}{{17}} - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{{14}}.\dfrac{{23}}{{17}} + \dfrac{{ - 15}}{{14}}.\dfrac{{11}}{{17}} - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{{14}}.\left( {\dfrac{{23}}{{17}} + \dfrac{{11}}{{17}}} \right) - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{{14}}.\dfrac{{34}}{{17}} - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{{14}}.2 - \dfrac{6}{7}\\ = \dfrac{{ - 15}}{7} - \dfrac{6}{7}\\ = \dfrac{{ - 21}}{7} = - 3\end{array}\)

b) \(\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2}} \right):\dfrac{{17}}{{13}} + \left( {\dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right):\dfrac{{17}}{{13}}\)

\(\begin{array}{l} = \left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2}} \right).\dfrac{{13}}{{17}} + \left( {\dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right).\dfrac{{13}}{{17}}\\ = \dfrac{{13}}{{17}}.\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 3}}{2} + \dfrac{7}{2} + \dfrac{{ - 1}}{3}} \right)\\ = \dfrac{{13}}{{17}}.\left[ {\left( {\dfrac{{ - 5}}{3} + \dfrac{{ - 1}}{3}} \right) + \left( {\dfrac{{ - 3}}{2} + \dfrac{7}{2}} \right)} \right]\\ = \dfrac{{13}}{{17}}.\left( {\dfrac{{ - 6}}{3} + \dfrac{4}{2}} \right)\\ = \dfrac{{13}}{{17}}.\left( { - 2 + 2} \right)\\ = \dfrac{{13}}{{17}}.0 = 0\end{array}\)

c) \({3^2}.\dfrac{1}{{243}}{.81^2}.\dfrac{1}{{{3^3}}}\)

\(\begin{array}{l} = {3^2}.\dfrac{1}{{{3^5}}}.{\left( {{3^4}} \right)^2}.\dfrac{1}{{{3^3}}}\\ = {3^2}.\dfrac{1}{{{3^5}}}{.3^8}.\dfrac{1}{{{3^3}}}\\ = \dfrac{{{3^2}{{.3}^8}}}{{{3^5}{{.3}^3}}} = \dfrac{{{3^{2 + 8}}}}{{{3^{5 + 3}}}}\\ = \dfrac{{{3^{10}}}}{{{3^8}}} = {3^{10 - 8}} = {3^2} = 9\end{array}\)

d) \(\left( {{{4.2}^5}} \right):\left( {{2^3}.\dfrac{1}{{16}}} \right)\)

\(\begin{array}{l} = \left( {{2^2}{{.2}^5}} \right):\left( {{2^3}.\dfrac{1}{{{2^4}}}} \right)\\ = {2^{2 + 5}}:\dfrac{{{2^3}}}{{{2^4}}} = {2^7}:\dfrac{1}{2}\\ = {2^7}.2 = {2^{7 + 1}}\\ = {2^8} = 256\end{array}\)

Bài 2

a) \(\left( { - 0,2} \right) - x.\dfrac{1}{6} = \dfrac{2}{3}\)

\(\begin{array}{l}\dfrac{{ - 1}}{5} - x.\dfrac{1}{6} = \dfrac{2}{3}\\ - x.\dfrac{1}{6} = \dfrac{2}{3} - \dfrac{{ - 1}}{5}\\ - x.\dfrac{1}{6} = \dfrac{{10}}{{15}} + \dfrac{3}{{15}}\\ - x.\dfrac{1}{6} = \dfrac{{13}}{{15}}\\ - x = \dfrac{{13}}{{15}}:\dfrac{1}{6} = \dfrac{{13}}{{15}}.6\\ - x = \dfrac{{26}}{5}\\x = \dfrac{{ - 26}}{5}\end{array}\)

Vậy \(x = \dfrac{{ - 26}}{5}\)

b) \(\left( {\dfrac{1}{3}x - \dfrac{8}{{13}}} \right).\left( {2,5 + \dfrac{{ - 7}}{5}:x} \right) = 0\)

Trường hợp 1:

\(\begin{array}{l}\dfrac{1}{3}x - \dfrac{8}{{13}} = 0\\\dfrac{1}{3}x = \dfrac{8}{{13}}\\x = \dfrac{8}{{13}}:\dfrac{1}{3}\\x = \dfrac{8}{{13}}.3\\x = \dfrac{{24}}{{13}}\end{array}\)

Trường hợp 2:

\(\begin{array}{l}2,5 + \dfrac{{ - 7}}{5}:x = 0\\\dfrac{{ - 7}}{5}:x = - 2,5\\x = \dfrac{{ - 7}}{5}:\left( { - 2,5} \right) = \dfrac{{ - 7}}{5}:\dfrac{{\left( { - 5} \right)}}{2}\\x = \dfrac{{ - 7}}{5}.\dfrac{2}{{\left( { - 5} \right)}}\\x = \dfrac{{14}}{{25}}\end{array}\)

Vậy \(x \in \left\{ {\dfrac{{24}}{{13}};\dfrac{{14}}{{25}}} \right\}\)

c) \(5.\left( {\dfrac{1}{{\sqrt {25} }} - x} \right) - \sqrt {\dfrac{1}{{81}}} = \dfrac{{ - 1}}{9}\)

\(\begin{array}{l}5.\left( {\dfrac{1}{5} - x} \right) - \dfrac{1}{9} = \dfrac{{ - 1}}{9}\\5.\left( {\dfrac{1}{5} - x} \right) = \dfrac{{ - 1}}{9} + \dfrac{1}{9}\\5.\left( {\dfrac{1}{5} - x} \right) = 0\\\dfrac{1}{5} - x = 0\\x = \dfrac{1}{5}\end{array}\)

Vậy \(x = \dfrac{1}{5}\)

d)

\(\begin{array}{l}\left| x \right| - \dfrac{{23}}{{17}} = 0\\\left| x \right| = \dfrac{{23}}{{17}}\end{array}\)

\(\left[ {\begin{array}{*{20}{c}}{x = \dfrac{{23}}{{17}}}\\{x = \dfrac{{ - 23}}{{17}}}\end{array}} \right.\)

Vậy \(x \in \left\{ {\dfrac{{23}}{{17}};\dfrac{{ - 23}}{{17}}} \right\}\)

Bài 3

Cách giải:

a) Diện tích xung quanh của chiếc khay nhựa dạng hình hộp chữ nhật là:

\(2.\left( {27 + 20} \right).10 = 940\,\left( {c{m^2}} \right)\)

b) Diện tích nhựa làm chiếc khay bằng tổng diện tích của các mặt xung quanh và mặt đáy.

Diện tích mặt đáy của chiếc khay là:

\(27.20 = 540\,\left( {c{m^2}} \right)\)

Diện tích nhựa để làm chiếc khay là:

\(940 + 540 = 1\,480\,\left( {c{m^2}} \right)\)

c) Thể tích nước khay nhựa có thể chứa được là:

\(20.27.10 = 5\,400\,\left( {c{m^3}} \right)\)

Bài 4

Cách giải:

a) Gọi tỉ lệ phần trăm chi phí gạch là x\% (điều kiện: x > 0)

Vì chi phí giám sát thi công, thép, gạch bằng nhau nên tỉ lệ phần trăm của chi phí giám sát thi công, thép là \(x\%\)

Ta có:

\(\begin{array}{l}x + x + x + 20\% + 25\% + 10\% = 100\% \\3x + 55\% = 100\% \\3x = 100\% - 55\% \\3x = 45\% \\x = 45\% :3\\x = 15\% \end{array}\)

Vậy chi phí trả tiền gạch chiếm 15% .

b) Chi phí bác An trả tiền công là: \(2,5.25\% = \dfrac{{25}}{{10}}.\dfrac{{25}}{{100}} = \dfrac{5}{8}\) = 0,625 (tỉ) = 625 (triệu đồng)

Bài 5

Hai \(\angle AOB\) và \(\angle CKD\) là hai góc có cạnh tương ứng song song cùng nhọn hoặc cùng tù nên \(\angle AOB = \angle CKD\) (1)

Vì Ox là tia phân giác của góc \(\angle AOB\) nên \(\angle {O_1} = \dfrac{1}{2}\angle AOB\) (2)

\(Ky\) là tia phân giác của góc \(\angle CKD\) nên \(\angle {K_1} = \dfrac{1}{2}\angle CKD\) (3)

Từ (1), (2) và (3) suy ra \(\angle {O_1} = \angle {K_1}\)

Mặt khác, vì \(OB//K{\rm{D}}\) nên \(\angle {H_1} = \angle {K_1}\) (so le trong)

Do đó, \(\angle {O_1} = \angle {H_1}\left( { = \angle {K_1}} \right)\).

Mà hai góc \(\angle {O_1};\angle {H_1}\) ở vị trí so le trong

Do đó \(Ox//Ky\) (dấu hiệu nhận biết hai đường thẳng song song)

Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo - Đề 3

Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo - Đề 4

Đề thi cuối học kì 1 Toán 7 Chân trời sáng tạo - Đề 5