35 Bài Tập Hệ Thức Lượng Trong Tam Giác Có Hướng Dẫn

Trang chủ » Bài Tập Hệ Thức Lượng Trong Tam Giác Toán 10 » 35 Bài Tập Hệ Thức Lượng Trong Tam Giác Có Hướng Dẫn

Có thể bạn quan tâm

35 bài tập hệ thức lượng trong tam giác có hướng dẫn Bài tập Toán lớp 10 có đáp án Bài trước Tải về Bài sau Lớp: Lớp 10 Môn: Toán Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

35 bài tập hệ thức lượng trong tam giác

  • Nhắc lại công thức hệ thức lượng trong tam giác
    • a. Định lí cosin
    • b. Tính độ dài đường trung tuyến của tam giác
    • c. Định lí sin
    • d. Công thức diện tích tam giác 
  • Bài tập hệ thức lượng trong tam giác 

Hệ thức lượng trong tam giác là một phần quan trọng của chương trình Toán lớp 10, giúp học sinh nắm vững mối quan hệ giữa các cạnh, góc và đường cao trong tam giác. Nắm chắc kiến thức này sẽ hỗ trợ giải nhanh các bài toán hình học và vận dụng trong nhiều dạng đề thi. Bài viết này tổng hợp 35 bài tập hệ thức lượng trong tam giác kèm hướng dẫn chi tiết, giúp các em vừa rèn kỹ năng vừa củng cố lý thuyết một cách hiệu quả.

Nhắc lại công thức hệ thức lượng trong tam giác

a. Định lí cosin

Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai góc còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.

Ta có hệ thức sau:

a^2=b^2+c^2-2.b.c.cos\hat{A}\(a^2=b^2+c^2-2.b.c.cos\hat{A}\)

b^2=a^2+c^2-2.a.c.cos\hat{B}\(b^2=a^2+c^2-2.a.c.cos\hat{B}\)

c^2=a^2+b^2-2a.b.cos\hat{C}\(c^2=a^2+b^2-2a.b.cos\hat{C}\)

b. Tính độ dài đường trung tuyến của tam giác

Cho tam giác ABC có cạnh AB = c, AC = b, BC = a. Gọi độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C của tam giác ABC là: m_a,m_b,m_c\(m_a,m_b,m_c\) ta có: 

m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}\(m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}\)

m^2_b=\dfrac{a^2+c^2}{2}-\dfrac{b^2}{4}\(m^2_b=\dfrac{a^2+c^2}{2}-\dfrac{b^2}{4}\)

m^2_c=\dfrac{b^2+a^2}{2}-\dfrac{c^2}{4}\(m^2_c=\dfrac{b^2+a^2}{2}-\dfrac{c^2}{4}\)

c. Định lí sin

Trong tam giác ABC bất kì, tỉ số giữa cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là:

\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)

Với R là bán kính đường tròn ngoại tiếp tam giác

d. Công thức diện tích tam giác 

Giả sử h_a,h_b,h_c\(h_a,h_b,h_c\) là các đường cao  lần lượt kẻ từ đỉnh A, B, C của tam giác ABC.

Diện tích tam giác ABC được tính theo một trong các công thức sau:

\begin{align} & S=\frac{1}{2}.{{h}_{a}}.BC=\frac{1}{2}{{h}_{b}}.AC=\frac{1}{2}{{h}_{c}}.AB \\ & S=\frac{1}{2}a.b.\sin \widehat{C}=\frac{1}{2}a.c.\sin \widehat{B}=\frac{1}{2}c.b.\sin \widehat{A} \\ & S=\frac{a.b.c}{4.R} \\ & S=p.r \\ & S=\sqrt{p.\left( p-a \right)\left( p-b \right)\left( p-c \right)} \\ \end{align}\(\begin{align} & S=\frac{1}{2}.{{h}_{a}}.BC=\frac{1}{2}{{h}_{b}}.AC=\frac{1}{2}{{h}_{c}}.AB \\ & S=\frac{1}{2}a.b.\sin \widehat{C}=\frac{1}{2}a.c.\sin \widehat{B}=\frac{1}{2}c.b.\sin \widehat{A} \\ & S=\frac{a.b.c}{4.R} \\ & S=p.r \\ & S=\sqrt{p.\left( p-a \right)\left( p-b \right)\left( p-c \right)} \\ \end{align}\)

Với p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC

Bài tập hệ thức lượng trong tam giác 

Bài 1. Cho ΔABC có AB = 12, BC = 15, AC = 13

a. Tính số đo các góc của ΔABC

b. Tính độ dài các đường trung tuyến của ΔABC

c. Tính diện tích tam giác ABC, bán kính đường tròn nội tiếp, bán kính đường tròn ngoại tiếp tam giác ABC

d. Tính độ dài đường cao nối từ các đỉnh của tam giác ABC

Hướng dẫn giải

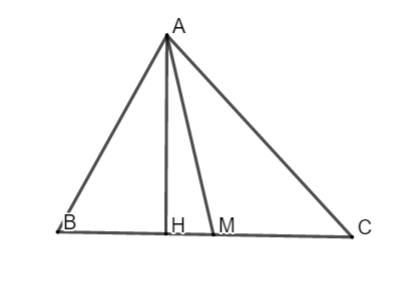
35 bài tập hệ thức lượng trong tam giác có hướng dẫn

a. Áp dụng hệ thức lượng trong tam giác ta có:

Từ khóa » Bài Tập Hệ Thức Lượng Trong Tam Giác Toán 10