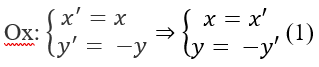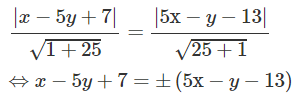5 Câu Hỏi Trắc Nghiệm Thuộc Giải SBT Bài 3: Phép đối Xứng Trục

Trang chủ » Phép đối Xứng Trục Sbt » 5 Câu Hỏi Trắc Nghiệm Thuộc Giải SBT Bài 3: Phép đối Xứng Trục

Có thể bạn quan tâm

Đăng nhập Facebook GOOGLE Google IMG

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Mục lục

  • Chương 1: Hàm số lượng giác và phương trình lượng giác
  • Chương 2: Tổ hợp - xác suất
  • Chương 3: Dãy số - Cấp số cộng và cấp số nhân
  • Chương 4: Giới hạn
  • Chương 5: Đạo hàm
  • Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
  • Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
  • Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
  • ĐỀ THI TOÁN 11
  • TRẮC NGHIỆM TỔNG HỢP TOÁN 11
  • CHUYÊN ĐỀ TOÁN 11
  • Chương I. Hàm số lượng giác và phương trình lượng giác
Mục lục Trang chủ Lớp 11 Toán Giải SBT Toán 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

Giải SBT Toán 11 Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng

  • Đề số 1
  • Đề số 2
  • Đề số 3
  • Đề số 4
  • Đề số 5
  • Đề số 6
  • Đề số 7
  • Đề số 8
  • Đề số 9
  • Đề số 10

Giải SBT Bài 3: Phép đối xứng trục

  • 2984 lượt thi

  • 5 câu hỏi

  • 30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x2 + y2 − 2x + 4y – 4 = 0. Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox

Xem đáp án

Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox . Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0. Từ đó suy ra phương trình của d' là

3x − 2y – 6 = 0

Thay (1) vào phương trình của (C) ta được x'2 + y'2 − 2x′ + 4y′ − 4 = 0 . Từ đó suy ra phương trình của (C') là

(x − 1)2 + (y − 2)2 = 9.

Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3, từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là (x − 1)2 + (y − 2)2 = 9

Câu 2:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình x − 5y + 7 = 0 và đường thẳng d’ có phương trình

5x – y – 13 = 0. Tìm phép đối xứng trục biến d thành d’.

Xem đáp án

Dễ thấy d và d' không song song với nhau. Do đó trục đối xứng Δ của phép đối xứng biến d thành d' chính là đường phân giác của góc tạo bởi d và d'. Từ đó suy ra Δ có phương trình:

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Từ đó tìm được hai phép đối xứng qua các trục:

∆1 có phương trình: x + y – 5 = 0,

∆2 có phương trình: x – y – 1 = 0.

Câu 3:

Tìm các trục đối xứng của hình vuông

Xem đáp án

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Cho hình vuông ABCD. Gọi F là phép đối xứng trục d biến hình vuông đó thành chính nó. Lí luận tương tự, ta thấy A chỉ có thể biến thành các điểm A, B, C hoặc D

- Nếu A biến thành chính nó thì C chỉ có thể biến thành chính nó và B biến thành D. Từ đó suy ra F là phép đối xứng qua trục AC

- Nếu A biến thành B thì d là đường trung trực của AB. Khi đó C biến thành D.

Các trường hợp khác lập luận tương tự. Do đó hình vuông ABCD có bốn trục đối xứng là các đường thẳng AC, BD và các đường trung trực của AB và BC.

Câu 4:

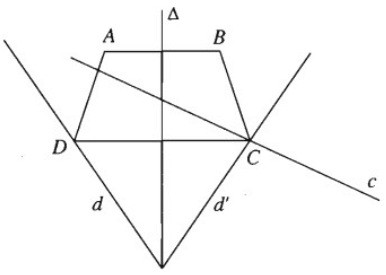
Cho hai đường thẳng c, d cắt nhau và hai điểm A, B không thuộc hai đường thẳng đó. Hãy dựng điểm C trên c, điểm D trên d sao cho tứ giác ABCD là hình thang cân nhận AB là một cạnh đáy ( không cần biện luận ).

Xem đáp án

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Ta thấy rằng B, C theo thứ tự là ảnh của A, D qua phép đối xứng qua đường trung trực của cạnh AB, từ đó suy ra cách dựng:

- Dựng đường trung trực Δ của đoạn ab

- Dựng d' là ảnh của d qua phép đối xứng qua trục Δ.

Gọi C = d′ ∩ c.

- Dựng D là ảnh của C qua phép đối xứng qua trục Δ.

Câu 5:

Cho đường thẳng d và hai điểm A, B không thuộc d nhưng nằm cùng phía đối với d. Tìm trên d điểm M sao cho tổng các khoảng cách từ đó đến A và B là bé nhất.

Xem đáp án

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Gọi B' là ảnh của B qua phép đối xứng qua trục d. Khi đó với mỗi điểm M thuộc d

MA + MB = MA + MB′ nên MA + MB′ bé nhất ⇔ A, M, B′ thẳng hàng.

Tức là M = (AB′) ∩ d.

Bắt đầu thi ngay

Bài thi liên quan

  • Giải SBT Bài 1: Phép biến hình - Bài 2: Phép tịnh tiến

    • 5 câu hỏi

    • 30 phút

  • Giải SBT Bài 4: Phép đối xứng tâm

    • 4 câu hỏi

    • 30 phút

  • Giải SBT Bài 5: Phép quay

    • 4 câu hỏi

    • 30 phút

  • Giải SBT Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

    • 4 câu hỏi

    • 30 phút

  • Giải SBT Bài 7: Phép vị tự

    • 4 câu hỏi

    • 30 phút

  • Giải SBT Bài 8: Phép đồng dạng

    • 4 câu hỏi

    • 30 phút

  • GiảI SBT Câu hỏi ôn tập chương 1

    • 12 câu hỏi

    • 30 phút

  • Đề toán tổng hợp chương 1

    • 6 câu hỏi

    • 30 phút

  • Giải SBT Câu hỏi trắc nghiệm chương 1

    • 30 câu hỏi

    • 30 phút

Từ khóa » Phép đối Xứng Trục Sbt