50 Bài Toán Về Tích Vô Hướng Và Tích Có Hướng Của Hai Vectơ (có đáp ...

Tích vô hướng và tích có hướng của hai vectơ và cách giải

I. LÝ THUYẾT

1. Tích vô hướng của hai vectơ

a) Tích vô hướng của hai vectơ

Trong không gian Oxyz, tích vô hướng của hai vectơ a→=a1; a2; a3 và b→=b1; b2; b3 được xác định bởi công thức:

a→.b→=a1b1+a2b2+a3b3

b) Ứng dụng của tích vô hướng

+ Cho vectơ a→=a1; a2; a3, khi đó độ dài của vectơ a→ được tính theo công thức:

a→=  a12+a22+a22

+ Cho hai điểm AxA; yA; zA và BxB; yB; zB. Khi đó khoảng cách giữa hai điểm A, B chính là độ dài của vectơ AB→. Do đó ta có

+ Cho vectơ a→=a1; a2; a3 và b→=b1; b2; b3. Khi đó góc giữa hai vectơ a→ và b→ được tính theo công thức:

cos(a→,  b→)  = a→.b→a→.b→  =  a1b1+a2b2+a3b3a12+a22+a32.b12+b22+b32

(với a→,  b→≠0→)

+ Hai vectơ vuông góc: Cho vectơ a→=a1; a2; a3 và b→=b1; b2; b3. Khi đó:

a→⊥b→   ⇔  a→.b→=0  ⇔a1b1+a2b2+a3b3=0

2. Tích có hướng của hai vectơ

a) Tích có hướng của hai vectơ

Trong không gian Oxyz cho hai vectơ a→=(a1;a2;a3), b→=(b1; b2; b3). Tích có hướng của hai vectơ a→ và b→, kí hiệu là a→,b→, được xác định bởi

 a→,b→  =  a2a3b2b3  ;  a3a1b3b1  ;  a1a2b1b2=a2b3−a3b2;a3b1−a1b3;a1b2−a2b1

Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

b) Tính chất của tích có hướng:

Từ đó suy ra 4 điểm A, B, C, D là 4 đỉnh của một tứ diện khi 3 vectơ AB→; AC→; AD→ không đồng phẳng hay AB→,AC→.AD→≠0 và 4 điểm A, B, C, D đồng phẳng khi AB→,AC→.AD→=0.

3. Ứng dụng của tích có hướng

II. PHƯƠNG PHÁP GIẢI VÀ VÍ DỤ MINH HỌA

1. Tích vô hướng của hai vectơ

Dạng 1: Tính biểu thức tọa độ tích vô hướng

Phương pháp giải:

Cho hai vectơ a→=a1; a2; a3 và b→=b1; b2; b3, khi đó: a→.b→=a1b1+a2b2+a3b3

Ví dụ 1: Trong không gian Oxyz, cho u→=−1;3;2, v→=−3;−1;2. Khi đó u→.v→ bằng

A. 10

B. 2

C. 3

D. 4

Hướng dẫn giải

u→.v→=−1.−3+3.−1+2.2=3−3+4=4

Chọn D.

Dạng 2: Tính độ dài của một vectơ

Phương pháp giải: Cho vectơ a→=a1; a2; a3, khi đó độ dài của vectơ a→ được tính theo công thức:

a→=  a12+a22+a22

Ví dụ 2: Trong không gian Oxyz cho vectơ a→=2; 4; 1. Độ dài vectơ a→ là

A. 21

B. 7

C. 21

D. 7

Hướng dẫn giải:

Độ dài vectơ a→ là:

a→=  22+42+12=21

Chọn A.

Dạng 3: Khoảng cách giữa hai điểm

Phương pháp giải: Cho hai điểm AxA; yA; zA và BxB; yB; zB. Khi đó khoảng cách giữa hai điểm A, B chính là độ dài của vectơ AB→. Do đó ta có

Ví dụ 3: Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; 2; 3), trên trục Oz lấy điểm M sao cho AM=5. Tọa độ của điểm M là

A. M (0; 0; 3).

B. M (0; 0; 2).

C. M (0; 0; -3).

D. M (0; 3; 0).

Hướng dẫn giải

Do M∈Oz⇒M (0; 0; m)

AM=0−12+0−22+m−32=(m−3)2+5

Mặt khác AM=5 nên

(m−3)2+5=5⇔m−32+5=5

⇔m – 3 = 0 ⇔m = 3

Suy ra M (0; 0; 3).

Chọn A.

Dạng 4: Góc giữa hai vectơ

Phương pháp giải: Cho vectơ a→=a1; a2; a3 và b→=b1; b2; b3. Khi đó góc giữa hai vectơ a→ và b→ được tính theo công thức:

cos(a→,  b→)  = a→.b→a→.b→ =  a1b1+a2b2+a3b3a12+a22+a32.b12+b22+b32

(với a→,  b→≠0→)

Ví dụ 4: Trong không gian Oxyz, cho bốn điểm A (1; 0; 0), B (0; 1; 0), C (0; 0; 1) và D (-2; 1; -1). Tính góc giữa hai vectơ AB→ và CD→.

A. 450

B. 600

C. 900

D. 1350

Hướng dẫn giải

Gọi φ là góc tạo bởi hai vectơ AB→ và CD→.

Ta có:

AB→=−1;1;0,  CD→=−2;1;−2

Khi đó:

cosφ=cosAB→,CD→=−1.−2+1.1+0.−2−12+12+02.−22+12+−22=12⇒φ=450

Chọn A.

Dạng 5: Tìm điều kiện để hai vectơ vuông góc

Phương pháp giải: Cho vectơ a→=a1; a2; a3 và b→=b1; b2; b3. Khi đó:

a→⊥b→   ⇔  a→.b→=0  ⇔a1b1+a2b2+a3b3=0

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, cho các vec tơa→=−1;1;0,b→=1;1;0 và c→=1;1;1. Mệnh đề nào dưới đây sai?

A. c→⊥b→

B. c→=3

C. a→⊥b→

D. a→=2

Hướng dẫn giải

Chọn A.

2. Tích có hướng của hai vectơ

Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương.

Dạng 1: Tính tích có hướng của hai vectơ

Phương pháp giải: Cho hai vectơ a→=a1; a2; a3 và b→=b1; b2; b3, khi đó:

 a→,b→  =  a2a3b2b3  ;  a3a1b3b1  ;  a1a2b1b2=a2b3−a3b2;a3b1−a1b3;a1b2−a2b1

Ví dụ 1: Trong không gian với hệ trục tọa độ Oxyz, cho a→=3;2;1, b→=3;2;5. Khi đó a→,b→ có tọa độ bằng

A. 8;−12;5

B. 8;−12;0

C. 0;8;12

D. 0;8;−12

Hướng dẫn giải

a→=3;2;1b→=3;2;5⇒a→,b→=2.5−2.1;  1.3−3.5;  3.2−3.2=8; −12; 0

Chọn B.

Dạng 2: Tìm điều kiện để ba vectơ đồng phẳng

Phương pháp giải: a→,  b→ và c→ đồng phẳng [a→,  b→] .c→=0

Ví dụ 2: Trong không gian với hệ tọa độ Oxyz cho vectơ a→=1;m;2;  b→=m+1;2;1;  c→=0;m−2;2. Giá trị của m để a→,  b→,  c→ đồng phẳng là

A. 25

B. −25

C. 15

D. 1.

Hướng dẫn giải

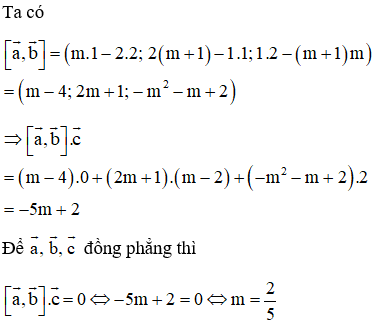
Chọn A.

Dạng 3: Tính diện tích một số hình phẳng

Phương pháp giải:

Áp dụng các công thức sau:

+) Diện tích hình bình hành ABCD:

SABCD=AB→,AD→

+) Diện tích tam giác ABC:

SABC=12AB→,  AC→

Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với A (1; 2; 1), B (2; 1; 3) và C (3; 2; 2). Diện tích tam giác ABC bằng

A. 112

B. 3

C. 132

D. 142

Hướng dẫn giải

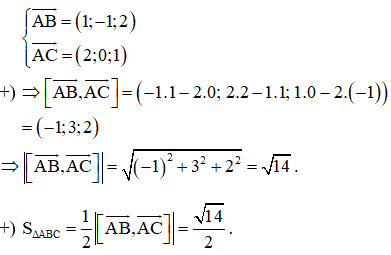
Chọn D.

Dạng 4: Tính thể tích khối hộp và tứ diện

Phương pháp giải:

Áp dụng các công thức sau:

+) Thể tích khối hộp ABCD. A’B’C’D’:

VABCD.A'B'C'D'  =  [AB→,  AD→].AA'→

+) Thể tích tứ diện ABCD:

VABCD=16[AB→,  AC→] .AD→

Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với A (1; 2; 1), B (2; 1; 3), C (3; 2; 2), D (1; 1; 1). Thể tích của tứ diện ABCD bằng

A. 1

B. 2

C. 12

D. 3.

Hướng dẫn giải

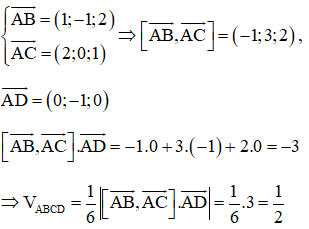
Chọn C.

III. BÀI TẬP ÁP DỤNG

Câu 1: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1; 0; -2), B (2; 1; -1). Độ dài của đoạn thẳng AB là

A. 2 

B. 18

C. 27

D. 3

Câu 2: Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ a→=1; −2; 0 và b→=−2; 3;1. Khẳng định nào sau đây là sai?

A. a→.b→=−8

B. a→+b→=−1; 1; −1

C. b→=14

D. 2a→=2; −4; 0

Câu 3: Trong không gian với hệ tọa độ Oxyz, cho hai vectơ a→=2;4;−2 và b→=3;−1;6. TínhP=a→.b→.

A. P = -10

B. P = -40

C. P = 16

D. P = -34

Câu 4: Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ a→=2;1;0 vàb→=−1;0;−2. Tính cosa→,b→.

A. cosa→,b→=−225

B. cosa→,b→=−25

C. cosa→,b→=225

D. cosa→,b→=25

Câu 5: Trong không gian với hệ trục tọa độ Oxyz, cho a→=1;−2;1,b→=2;−4;2. Khi đó a→,b→ có tọa độ bằng

A. (0 ; 0 ; 0).

B. (1 ; 1 ; 1)

C. (2 ; 8 ; 2)

D. (1 ; -2 ; 1).

Câu 6: Cho bốn véc tơ a→=−1;1;0,b→=1;1;0 ,c→=1;1;1, d→=2;0;1. Chọn mệnh đề đúng.

A.a→, b→, c→ đồng phẳng.

B. a→, b→, d→ đồng phẳng.

C. a→, c→, d→ đồng phẳng.

D. d→, b→, c→ đồng phẳng.

Câu 7: Trong không gian với hệ tọa độ Oxyz cho tam giác ABC biết A (1; 1; 1), B (4; 3; 2), C (5; 2; 1). Diện tích tam giác ABC là

A. 424

B. 42

C. 242

D. 422

Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD có A (1; 0; 1), B (2; 0; -1), C (0; 1; 3), D (3; 1; 1). Thể tích khối tứ diện ABCD là

A.V=23

B. V=43

C. V = 4

D. V = 2.

Câu 9: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD. A’B’C’D’ có A (-1; 0; 2), B (1; 1; -1), D (0; 1; 1), A’ (2; -1; 0). Thể tích V của khối hình hộp ABCD. A’B’C’D’ là

A. V = 1.

B. V = 4.

C. V = 5.

D. V = 6.

Câu 10: Cho ba vectơ a→=4;2;5,b→=3;1;3,c→=2;0;1. Chọn mệnh đề đúng:

A. Ba vectơ đồng phẳng

B. Ba vectơ không đồng phẳng.

C. Ba vectơ cùng phương

D. c→=a→,b→

ĐÁP ÁN

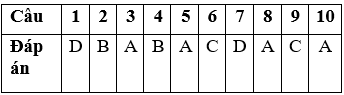
Xem thêm các dạng bài tập Toán lớp 12 có đáp án và lời giải chi tiết khác:

Các bài toán về phương trình mặt phẳng và cách giải

Các dạng toán về phương trình đường thẳng và cách giải

Các dạng toán về phương trình mặt cầu và cách giải

Bài toán về vị trí tương đối trong tọa độ không gian và cách giải

Các bài toán về góc trong không gian và cách giải