Áp Dụng Quy Tắc I, Hãy Tìm Các điểm Cực Trị Của Hàm Số Sau

Bài 1. Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm số sau :

 a) \(y{\rm{ }} = {\rm{ }}2{x^{3}} + {\rm{ }}3{x^2}-{\rm{ }}36x{\rm{ }}-{\rm{ }}10\) ;

b) \(y{\rm{ }} = {\rm{ }}x{^4} + {\rm{ }}2{x^2}-{\rm{ }}3\) ;

c) \(y = x + {1 \over x}\)

d) \(y{\rm{ }} = {\rm{ }}{x^3}{\left( {1{\rm{ }}-{\rm{ }}x} \right)^{2}}\);

 e) \(y = \sqrt {{x^2} - x + 1}\)

a) Tập xác định: \(D = \mathbb R\)

\(\eqalign{ & y’ = 6{{\rm{x}}^2} + 6{\rm{x}} - 36;y’ = 0 \cr & \Leftrightarrow \left[ \matrix{ x = 2\left( {y = - 54} \right) \hfill \cr x = - 3\left( {y = 71} \right) \hfill \cr} \right. \cr} \)

Bảng biến thiên:

Hàm số đạt cực trị tại \(x = -3\) và  \(y\)CĐ \(= 71\)

Hàm số đạt cực tiểu tại \(x = 2\) và \(y\)CT \(= -54\)

b) Tập xác định: \(D =\mathbb R\)

\(y’ = 4{{\rm{x}}^3} + 4{\rm{x}} = 4{\rm{x}}\left( {{x^2} + 1} \right)\);

\(y’ = 0 \Leftrightarrow x = 0\left( {y =  - 3} \right)\)

Bảng biến thiên:

Hàm số có điểm cực tiểu tại \(x = 0\) và \(y\)CT \(= -3\)

Advertisements (Quảng cáo)

c) Tập xác định: \(D = \mathbb R\)\ { 0 }

\(\eqalign{ & y’ = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}};y’ = 0 \cr & \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \matrix{ x = 1\left( {y = 2} \right) \hfill \cr x = - 1\left( {y = - 2} \right) \hfill \cr} \right. \cr}\)

Bảng biến thiên

Hàm số đạt cực đại tại \(x = -1\), \(y\)CĐ \(= -2\)

Hàm số đạt cực tiểu tại \(x = 1\), \(y\)CT  \(= 2\)

d) Tập xác định \(D = \mathbb R\)

\( y’ = 3{{\rm{x}}^2}{\left( {1 - x} \right)^2} - 2{{\rm{x}}^3}\left( {1 - x} \right) \)

     \(= {x^2}\left( {1 - x} \right)\left( {3 - 5{\rm{x}}} \right)\)

\(\eqalign{ & y’ = 0 \Leftrightarrow \left[ \matrix{ x = 1\left( {y = 0} \right) \hfill \cr x = {3 \over 5}\left( {y = {{108} \over {3125}}} \right) \hfill \cr x = 0 \hfill \cr} \right. \cr} \)

Bảng biến thiên:

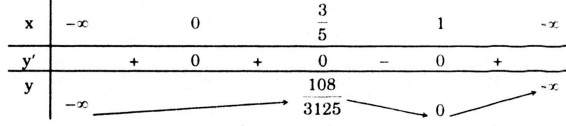
Hàm số đạt cực đại tại \(x = {3 \over 5};y = {{108} \over {3125}}\)

Hàm số đạt cực tiểu tại \(x = 1\), \(y\)CT =\( 0\)

e) Vì  \(x^2\) –\( x + 1 > 0, ∀  ∈ \mathbb R\) nên tập xác định : \(D = \mathbb R\)

\(y’ = {{2{\rm{x}} - 1} \over {2\sqrt {{x^2} - x + 1} }};y = 0 \Leftrightarrow x = {1 \over 2}\left( {y = {{\sqrt 3 } \over 2}} \right)\)

Bảng biến thiên:

Hàm số đạt cực tiểu tại \(x = {1 \over 2};{y_{CT}} = {{\sqrt 3 } \over 2}\)