B D ⊥ ( S A C ) - . B. Tính Góc Giữa SB Và (SAD). C. Tính Côsin Của ...

Câu hỏi số 404061: Vận dụng

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng  (ABCD) và SA = 2a.

a. Chứng minh \(BD \bot (SAC)\).

b. Tính góc giữa SB và (SAD).

c. Tính côsin của góc tạo bởi hai mặt phẳng (SAC) và (SCD).

Quảng cáo

Xem lời giải Câu hỏi:404061 Phương pháp giải

a) Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\).

b) Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng kia.

Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.

c) Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

Giải chi tiết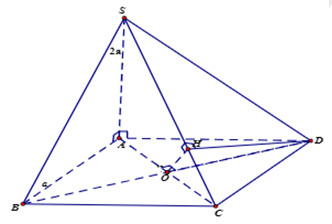

a) Vì ABCD là hình vuông nên \(AC \bot BD\).

Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot BD\).

Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).

b) Ta có: \(\left\{ \begin{array}{l}BA \bot AD\\BA \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BA \bot \left( {SAD} \right)\).

Suy ra SA là hình chiếu của SB lên (SAD).

\( \Rightarrow \angle \left( {SB;\left( {SAD} \right)} \right) = \angle \left( {SB;SA} \right) = \angle ASB\).

Xét tam giác vuông SAB có: \(\tan \angle ASB = \dfrac{{AB}}{{SA}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\)  \( \Rightarrow \angle ASB \approx {27^0}\).

Vậy góc giữa SB và (SAD) xấp xỉ \({27^0}\).

c) Gọi \(O = AC \cap BD\).

Trong (SAC) kẻ \(OH \bot SC\,\,\left( {H \in SC} \right)\).

Ta có: \(BD \bot \left( {SAC} \right)\,\,\left( {cmt} \right) \Rightarrow BD \bot SC\).

Khi đó ta có: \(\left\{ \begin{array}{l}SC \bot OH\\SC \bot BD\end{array} \right. \Rightarrow SC \bot \left( {BDH} \right) \Rightarrow SC \bot HD\).

Ta có: \(\left\{ \begin{array}{l}\left( {SAC} \right) \cap \left( {SCD} \right) = SC\\\left( {SAC} \right) \supset OH \bot SC\\\left( {SCD} \right) \supset DH \bot SC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SAC} \right);\left( {SCD} \right)} \right) = \angle \left( {OH;DH} \right)\).

Vì \(ABCD\) là hình vuông cạnh \(a\) nên \(AC = BD = a\sqrt 2 \) \( \Rightarrow OD = \dfrac{{a\sqrt 2 }}{2}\).

Ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD\), suy ra tam giác SCD vuông tại D.

Có: \(SD = \sqrt {S{A^2} + A{D^2}}  = \sqrt {4{a^2} + {a^2}}  = a\sqrt 5 \).

\(\begin{array}{l} \Rightarrow \dfrac{1}{{D{H^2}}} = \dfrac{1}{{S{D^2}}} + \dfrac{1}{{C{D^2}}} = \dfrac{1}{{5{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{6}{{5{a^2}}}.\\ \Rightarrow DH = \dfrac{{a\sqrt {30} }}{6}\end{array}\)

Xét \(\Delta COH\) và \(\Delta CSA\) có: \(\angle ACS\) chung, \(\angle CHO = \angle CAS = {90^0}\).

\( \Rightarrow \Delta COH \sim \Delta CSA\,\,\left( {g.g} \right)\).

\( \Rightarrow \dfrac{{OH}}{{SA}} = \dfrac{{OC}}{{SC}} \Rightarrow \dfrac{{OH}}{{2a}} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + 2{a^2}} }} \Rightarrow OH = \dfrac{{a\sqrt 3 }}{3}\).

Áp dụng định lí Cô-sin trong tam giác OHD có:

\(\begin{array}{l}\cos \angle OHD = \dfrac{{O{H^2} + D{H^2} - O{D^2}}}{{2OH.DH}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\dfrac{{{a^2}}}{3} + \dfrac{{5{a^2}}}{6} - \dfrac{{{a^2}}}{2}}}{{2.\dfrac{{a\sqrt 3 }}{3}.\dfrac{{a\sqrt {30} }}{6}}} = \dfrac{{\sqrt {10} }}{5} > 0\end{array}\)

\( \Rightarrow \angle OHD\) là góc nhọn nên \(\angle \left( {\left( {SAC} \right);\left( {SCD} \right)} \right) = \angle OHD\).  

Vậy \(\cos \angle \left( {\left( {SAC} \right);\left( {SCD} \right)} \right) = \dfrac{{\sqrt {10} }}{5}\).