Bài 1. Các định Nghĩa - SureTEST

1. Khái niệm vectơ

Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểm đầu, điểm B làm điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là một đoạn thẳng có hướng.

* Định nghĩa

Vectơ là một đoạn thẳng có hướng.

Vectơ có điểm đầu A, điểm cuối B được kí hiệu là $\overrightarrow {AB} $ và đọc là "vectơ AB". Để vẽ vectơ $\overrightarrow {AB} $ ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu mút B.

Vectơ còn được kí hiệu là $\overrightarrow a ,\overrightarrow b ,\overrightarrow x ,\overrightarrow y ,$ ...khi không cần chỉ rõ điểm đầu và điểm cuối của nó.

2. Vectơ cùng phương, vectơ cùng hướng

Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

* Định nghĩa

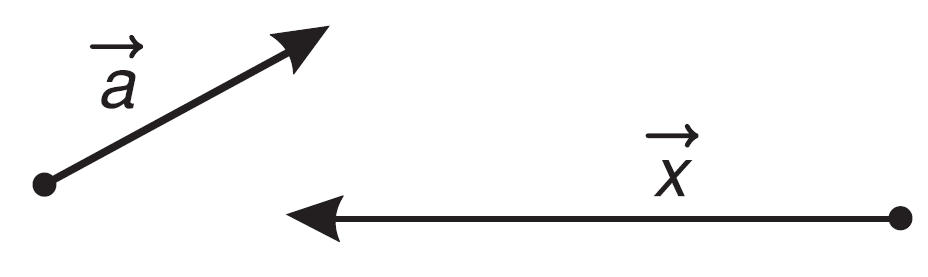
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Hai vectơ $\overrightarrow {AB} $ và $\overrightarrow {CD} $ cùng phương và có cùng hướng đi từ trái sang phải. Ta nói $\overrightarrow {AB} $ và $\overrightarrow {CD} $ là hai vectơ cùng hướng.

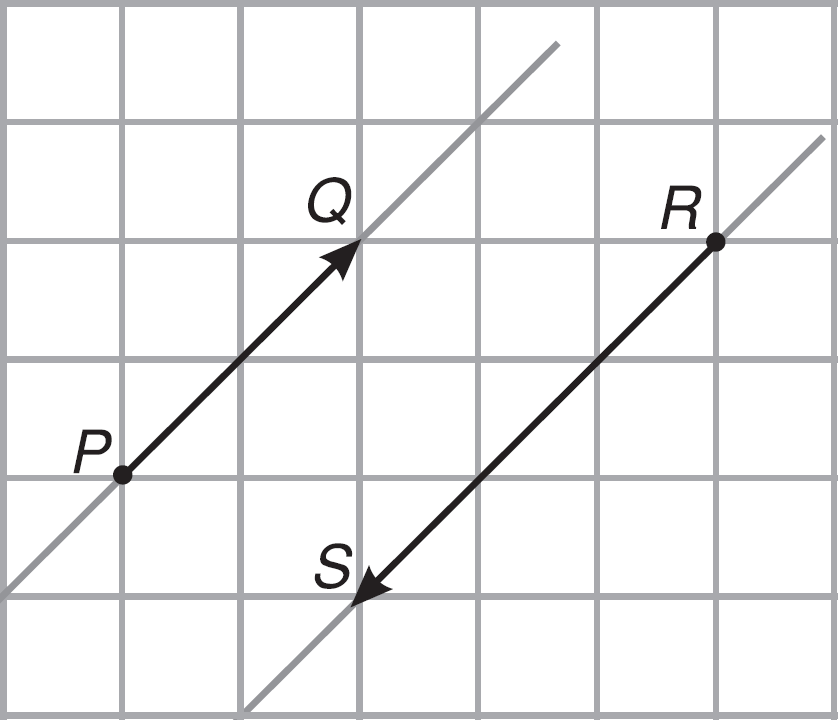
Hai vectơ $\overrightarrow {PQ} $ và $\overrightarrow {RS} $ cùng phương nhưng có hướng ngược nhau. Ta nói hai vectơ $\overrightarrow {PQ} $ và $\overrightarrow {RS} $ là hai vectơ ngược hướng.

Nhận xét

Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ $\overrightarrow {AB} $ và $\overrightarrow {AC} $ cùng phương.

3. Hai vectơ bằng nhau

Mỗi vectơ có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của

vectơ đó. Độ dài của $\overrightarrow {AB} $ được kí hiệu là $\left| {\overrightarrow {AB} } \right|$ , như vậy $\left| {\overrightarrow {AB} } \right| = AB$.

Vectơ có độ dài bằng 1 gọi là vectơ đơn vị.

Hai vectơ $\overrightarrow a $ và $\overrightarrow b $ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu $\vec a = \vec b$.

Chú ý

Khi cho trước vectơ ${\vec a}$ và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho $\overrightarrow {OA} = \vec a$.

4. Vectơ – không

Với một điểm A bất kì ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu là $\overrightarrow {AA} $ và gọi là vectơ - không.

Vectơ $\overrightarrow {AA} $ nằm trên mọi đường thẳng đi qua A, vì vậy ta quy ước vectơ - không cùng phương, cùng hướng với mọi vectơ. Ta cũng quy ước rằng $\overrightarrow {AA} = \vec 0$. Do đó có thể coi mọi vectơ - không đều bằng nhau.

Ta kí hiệu vectơ - không là $\overrightarrow 0 $. Như vậy $\overrightarrow 0 = \overrightarrow {AA} = \overrightarrow {BB} = ...$ với mọi điểm A, B...