Bài 1. Cung Và Góc Lượng Giác - SureTEST
I. Khái niệm cung và góc lượng giác
1. Đường tròn định hướng và cung lượng giác
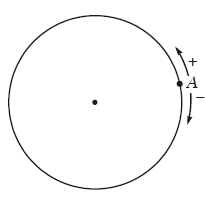
Đường tròn định hướng là một đường tròn trên đó ta đã chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại là chiều âm.
Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ làm chiều dương.
* Chú ý
Trên một đường tròn định hướng, lấy hai điểm A và B thì:
Kí hiệu $\mathop {AB}\limits^ \curvearrowright $ chỉ một cung lượng giác điểm đầu A, điểm cuối B.
2. Góc lượng giác
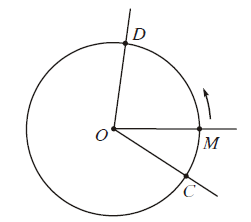
Trên một đường tròn định hướng, cho một cung lượng giác $\mathop {CD}\limits^ \curvearrowright $. Một điểm M chuyển động trên đường tròn từ C đến D tạo nên cung lượng giác $\mathop {CD}\limits^ \curvearrowright $ nói trên. Khi đó tia OM quay xung quanh gốc O từ vị trí OC tới vị trí OD. Ta nói tia OM tạo ra một góc lượng giác, có tia đầu là OC, tia cuối là OD. Kí hiệu góc lượng giác đó là (OC, OD).
3. Đường tròn lượng giác
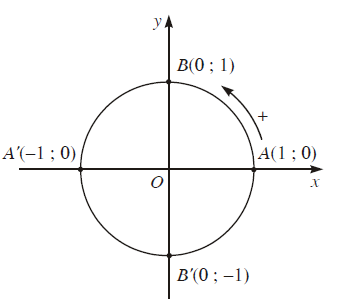
Trong mặt phẳng tọa độ Oxy vẽ đường tròn định hướng tâm O bán kính R = 1.
Đường tròn này cắt hai trục tọa độ tại bốn điểm $A\left( {1;0} \right),A'\left( { - 1;0} \right),B\left( {0;1} \right),B'\left( {0; - 1} \right)$. Ta lấy $A\left( {1;0} \right)$ làm điểm gốc của đường tròn đó.
Đường tròn xác định như trên được gọi là đường tròn lượng giác (gốc A).
II. Số đo của cung và góc lượng giác
1. Độ và rađian
a) Đơn vị rađian
Trên đường tròn tùy ý, cung có độ dài bằng bán kinh được gọi là cung có số đo 1 rad.
b) Quan hệ giữa độ và rađian
${1^0} = \frac{\pi }{{180}}rad$ và $1rad = {\left( {\frac{{180}}{\pi }} \right)^0}$
* Bảng chuyển đổi thông dụng
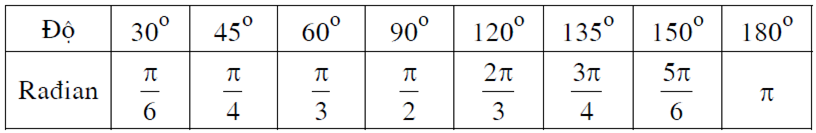
c) Độ dài của một cung tròn
Cung có số đo $\alpha $ rad của đường tròn đường kính R có độ dài
$l = R\alpha $
2. Số đo của một cung lượng giác
Số đo của một cung lượng giác $\mathop {AM}\limits^ \curvearrowright \left( {A \ne M} \right)$ là một số thực, âm hay dương.
Kí hiệu của số đo của cung $\mathop {AM}\limits^ \curvearrowright $ là sđ $\mathop {AM}\limits^ \curvearrowright $.
sđ $\mathop {AM}\limits^ \curvearrowright = \alpha + k2\pi ,k \in Z$
sđ $\mathop {AM}\limits^ \curvearrowright = {a^0} + k{360^0},k \in Z$
3. Số đo của một góc lượng giác
Số đo của góc lượng giác (OA, OC) là số đo của cung lượng giác $\mathop {AC}\limits^ \curvearrowright $ tương ứng.
4. Biểu diễn cung lượng giác trên đường tròn lượng giác
Để biểu diễn cung lượng giác có số đo $\alpha $ trên đường tròn lượng giác, ta chọn điểm A (1; 0) làm điểm đầu của cung vì vậy chỉ cần xác định điểm cuối M trên đường tròn lượng giác sao cho cung $\mathop {AM}\limits^ \curvearrowright $ có sđ $\mathop {AM}\limits^ \curvearrowright = \alpha $.
Từ khóa » đt Lượng Giác
-
Đường Tròn Lượng Giác - Một Số Kết Quả Cần Nhớ - Thayphu
-
[ Đường Tròn Lượng Giác ] Những Thông Tin Và Một Số Lưu ý Khi Dùng
-
Đường Tròn Lượng Giác Lớp 11-Những Kiến Thức Cơ Bản Không Thể ...
-
Vòng Tròn Lượng Giác
-
Vòng Tròn Lượng Giác Cơ Bản Và Hướng Dẫn Sử Dụng Chi Tiết
-
Đường Tròn Lượng Giác - Tỷ Mỷ Làm Toán. Độc Lập Suy Nghĩ.
-
Hướng Dẫn Sử Dụng đường Tròn Lượng Giác - YouTube
-
Cách Tính Sin Cos Bằng điện Thoại Samsung
-
Phương Pháp Đường Tròn Lượng Giác Vật Lý 12 - Kiến Guru
-
Biểu Diễn Góc Và Cung Lượng Giác
-
Công Thức Lượng Giác đầy đủ Nhất Cho Lớp 9, Lớp 10, Lớp 11
-
Công Thức Lượng Giác đầy đủ Từ A đến Z Và Cách Học ... - Pinterest
-
Hướng Dẫn Sử Dụng đường Tròn Lượng Giác