Bài 1. Giá Trị Lượng Giác Của Một Góc Bất Kì Từ 0 độ đến 180 độ

1. Định nghĩa

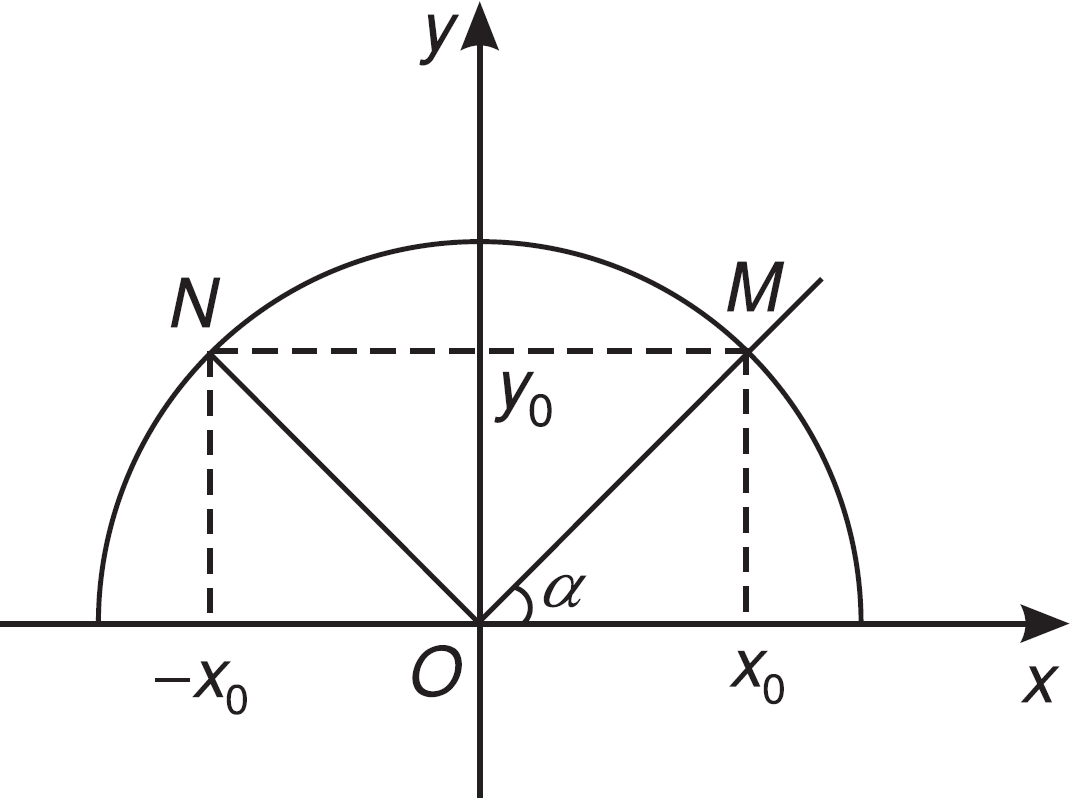
Với mỗi góc $\alpha $ (${0^0} \leqslant \alpha \leqslant {180^0}$) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho $\widehat {xOM} = \alpha $ và giả sử điểm M có toạ độ $M\left( {{x_0};{y_0}} \right)$. Khi đó ta định nghĩa :

* sin của góc $\alpha $ là ${y_0}$, kí hiệu $\sin \alpha = {y_0}$;

* côsin của góc $\alpha $ là ${x_0}$, kí hiệu $\cos \alpha = {x_0}$;

* tang của góc $\alpha $ là $\frac{{{y_0}}}{{{x_0}}}\left( {{x_0} \ne 0} \right)$, kí hiệu $\tan \alpha = \frac{{{y_0}}}{{{x_0}}}$;

* côtang của góc $\alpha $ là $\frac{{{x_0}}}{{{y_0}}}\left( {{y_0} \ne 0} \right)$, kí hiệu $\cot \alpha = \frac{{{x_0}}}{{{y_0}}}$.

Các số sin$\alpha $, cos$\alpha $, tan$\alpha $, cot$\alpha $ được gọi là các giá trị lượng giác của góc $\alpha $.

Chú ý

* Nếu $\alpha $ là góc tù thì cos$\alpha $< 0, tan$\alpha $< 0, cot$\alpha $< 0.

* tan$\alpha $ chỉ xác định khi $\alpha \ne \frac{\pi }{2} + k\pi $, cot$\alpha $ chỉ xác định khi $\alpha \ne k\pi ,k \in Z.$

2. Tính chất

Ta có dây cung NM song song với trục Ox và nếu $\widehat {xOM} = \alpha $ thì $\widehat {xON} = {180^0} - \alpha $.

Ta có ${y_M} = {y_N} = {y_0};{x_M} = - {x_N} = {x_0}$. Do đó:

$\begin{gathered} \sin \alpha = \sin \left( {{{180}^0} - \alpha } \right) \hfill \\ \cos \alpha = - \cos \left( {{{180}^0} - \alpha } \right) \hfill \\ \tan \alpha = - \tan \left( {{{180}^0} - \alpha } \right) \hfill \\ \cot \alpha = - \cot \left( {{{180}^0} - \alpha } \right) \hfill \\ \end{gathered} $

3. Giá trị lượng giác của các góc đặc biệt

Bảng giá trị lượng giác của các góc đặc biệt

Trong bảng, kí hiệu $\parallel $ để chỉ giá trị lượng giác không xác định.

Chú ý

Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác.

Chẳng hạn:

$\begin{gathered} \sin {120^0} = \sin \left( {{{180}^0} - {{60}^0}} \right) = \sin {60^0} = \frac{{\sqrt 3 }}{2} \hfill \\ \cos {135^0} = \cos \left( {{{180}^0} - {{45}^0}} \right) = - \cos {45^0} = - \frac{{\sqrt 2 }}{2} \hfill \\ \end{gathered} $

4. Góc giữa hai vectơ

a) Định nghĩa

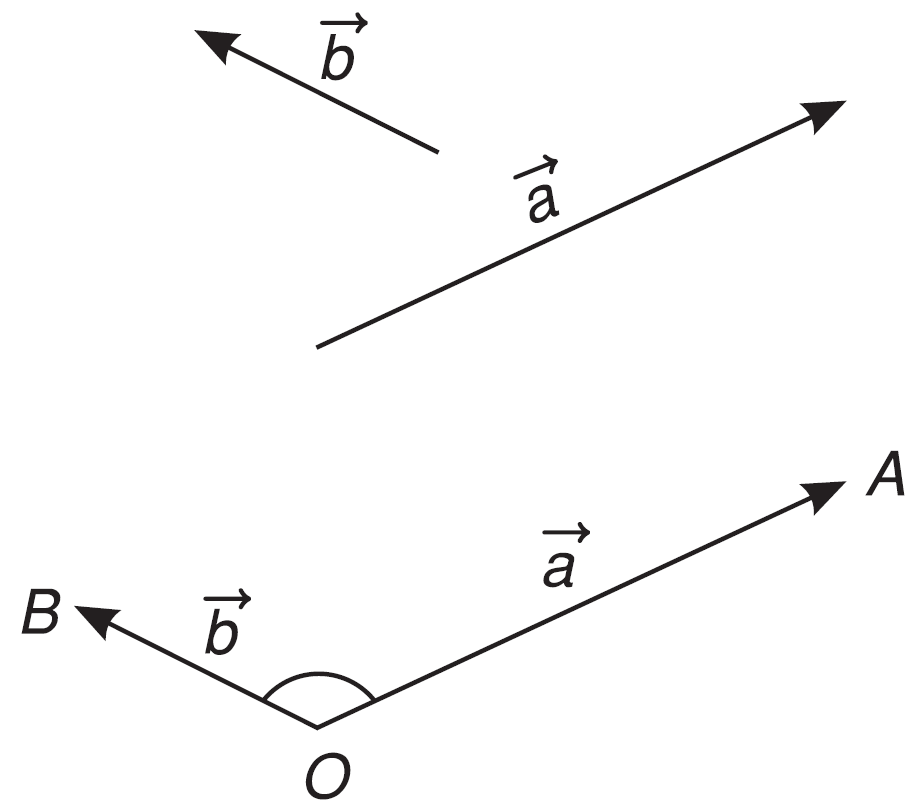
Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ đều khác vectơ $\overrightarrow 0 $. Từ một điểm O bất kì ta vẽ $\overrightarrow {OA} = \overrightarrow a $ và $\overrightarrow {OB} = \overrightarrow b $ . Góc $\widehat {AOB}$ với số đo từ ${0^0}$ đến ${180^0}$ được gọi là góc giữa hai vectơ $\overrightarrow a $ và $\overrightarrow b $. Ta kí hiệu góc giữa hai vectơ $\overrightarrow a $ và $\overrightarrow b $ là ($\overrightarrow a $, $\overrightarrow b $). Nếu ($\overrightarrow a $, $\overrightarrow b $) $ = {90^0}$ thì ta nói rằng $\overrightarrow a $ và $\overrightarrow b $ vuông góc với nhau, kí hiệu là $\overrightarrow a \bot \overrightarrow b $ hoặc $\overrightarrow b \bot \overrightarrow a $.

b) Chú ý

Từ định nghĩa ta có ($\overrightarrow a $, $\overrightarrow b $) = ($\overrightarrow b $, $\overrightarrow a $).

5. Sử dụng máy tính bỏ túi để tính giá trị lượng giác của một góc

Ta có thể sử dụng các loại máy tính bỏ túi để tính giá trị lượng giác của một góc, chẳng hạn đối với máy CASIO fx - 500MS cách thực hiện như sau :

a) Tính các giá trị lượng giác của gốc a

Sau khi mở máy ấn phím MODE nhiều lần để màn hình hiện lên dòng chữ ứng với các số sau đây :

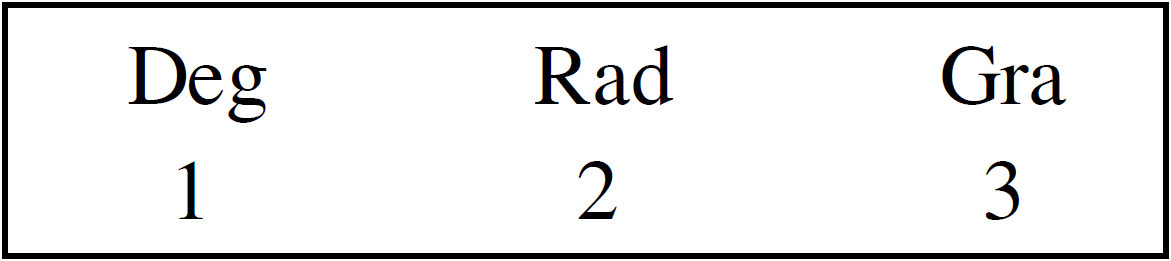
Sau đó ấn phím 1 để xác định đơn vị đo góc là “độ” và tính giá trị lượng giác của góc.

b) Xác định độ lớn của góc khi biết giá trị lượng giác của góc đó

Sau khi mở máy và chọn đơn vị đo góc, để tính góc x khi biết các giá trị lượng giác của góc đó.