Bài 1: Hệ Phương Trình Tuyến Tính - HOC247
Có thể bạn quan tâm
1. Dạng biểu diễn ma trận.
Ví dụ: Xét hệ 3 phương trình tuyến tính 4 ẩn số sau đây:
\(\left\{ \begin{array}{l} 2{x_1} - {x_2} + {x_3} - 3{x_4} = 1\\ {x_1} - 4{x_3} + 5{x_4} = - 2\\ - 2{x_2} + {x_4} = 0 \end{array} \right.\)
Đặt \(A = \left( {\begin{array}{*{20}{c}} 2&{ - 1}&1&{ - 3}\\ 1&0&{ - 4}&5\\ 0&{ - 2}&0&1 \end{array}} \right),\,X = ({x_1};{x_2};{x_3};{x_4}) = \left( \begin{array}{l} {x_1}\\ {x_2}\\ {x_3}\\ {x_4} \end{array} \right)\,\,và\,B = \left( \begin{array}{l} 1\\ - 2\\ 0 \end{array} \right)\)
Khi đó, hệ phương trình trên có thể viết lại dưới dạng ma trận là: AX = B.
Trong trường hợp tổng quát, ta xét hệ m phương trình tuyến tính n ẩn như sau:
\(\left\{ \begin{array}{l} {a_{11}}{x_1} + {a_{12}}{x_2} + .... + {a_{1n}}{x_n} = {b_1}\\ {a_{21}}{x_1} + {a_{22}}{x_2} + .... + {a_{2n}}{x_n} = {b_2}\\ ................................\\ {a_{m1}}{x_1} + {a_{m2}}{x_2} + .... + {a_{mn}}{x_n} = {b_m} \end{array} \right.\)
Đặt \(A = {({a_{{\rm{ij}}}})_{m\,x\,n}},\,X = \left( \begin{array}{l} {x_1}\\ .\\ .\\ .\\ {x_n} \end{array} \right),\,B = \left( \begin{array}{l} {b_1}\\ .\\ .\\ .\\ {b_n} \end{array} \right)\). Khi đó, hệ phương trình trên có thể viết lại dưới dạng ma trận là AX = B.
- Ma trận \(A_{m x n}\) gọi là ma trận hệ sổ của hệ phương trình.
- Ma trận \(\overline A = (A|B)\) gọi là ma trận hệ số mở rộng của hệ phương trình.
- X gọi là vectơ ẩn.
2. Giải hệ phương trình tuyến tính bằng phương pháp Gauss.
Một phương pháp thông dụng để giải hệ phương trình tuyến tính là phương pháp Gauss, đưa ma trận hệ số mở rộng \(\overline A \) về dạng bậc thang hay bậc thang thu gọn, nhờ các phép biến đổi sơ cấp trên dòng.
Ví dụ: Giải hệ phương trình tuyến tính
\(\left\{ \begin{array}{l} {x_1} - 2{x_2} - {x_3} = - 6\\ 2{x_1} - {x_2} + {x_3} = 3\\ {x_1} + {x_3} = 4 \end{array} \right.\,\,\,(I)\)
Giải:
Ma trận hệ số mở rộng của (I) là :
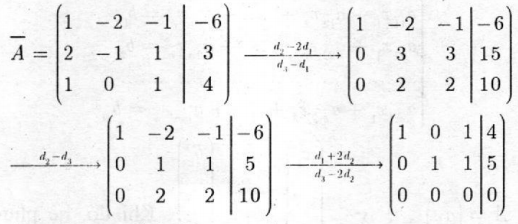
Ta có hệ phương trình (I) tương đương:
\(\left\{ \begin{array}{l} {x_1} + {x_3} = 4\\ {x_2} + {x_3} = 5 \end{array} \right.\,\,\,hay\,\,\left\{ \begin{array}{l} {x_1} = 4 - {x_3}\\ {x_2} = 5 - {x_3} \end{array} \right.\)
Cho \({x_3} = \alpha \in R\), nghiệm của hệ là \({x_1} = 4 - \alpha ,{x_2} = 5 - \alpha ,{x_3} = \alpha \)
Như thế, hệ phương trình có vô số nghiệm với nghiệm tổng quát là:
\(X = (4 - \alpha ;5 - \alpha ;\alpha );\alpha \in R\)
Ví dụ: Giải hệ phương trình tuyến tính
\(\left\{ \begin{array}{l} {x_1} - {x_2} = - 1\\ 2{x_1} + {x_2} - {x_3} = 1\\ {x_2} + {x_3} = 5 \end{array} \right.\,\,\,(I)\)
Giải
Ma trận hệ số mở rộng của (I) là:

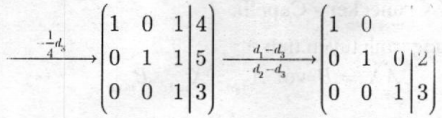
Ta có hệ phương trình tương đương \(\left\{ \begin{array}{l} {x_1} = 1\\ {x_2} = 2\\ {x_3} = 3 \end{array} \right.\)
Vậy hệ có nghiệm duy nhất X = (1;2;3)
Ví dụ: Giải hệ phương trình tuyến tính
\(\left\{ \begin{array}{l} {x_1} + {x_2} - 2{x_3} = 1\\ 2{x_1} + {x_3} = 0\\ 4{x_1} + 2{x_2} - 3{x_3} = 3 \end{array} \right.\,\,(I)\)
Giải: Ma trận hệ số mở rộng của (I) là
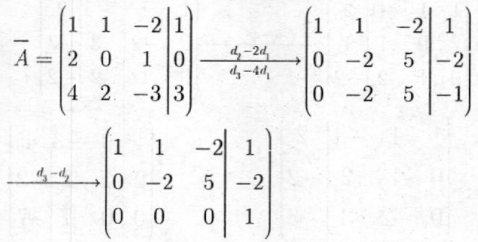
Ta có hệ phương trình tương đương: \(\left\{ \begin{array}{l} {x_1} + {x_2} - 2{x_3} = 1\\ - 2{x_2} + 5{x_3} = - 2\\ 0 = 1 \end{array} \right.\)
Vậy hệ phương trình vô nghiệm
3. Định lý Cronecker - Capelli
Xét hệ phương trình tuyến tính: AX = B với \({A_{m\,x\,n}},\,{X_{n\,\,x\,1}},\,{B_{m\,x\,1}}\)
Ta có:
- Hệ có nghiệm duy nhất \(\Leftrightarrow R(A) = R(\overline A ) = n\)
- Hệ có vô số nghiệm \(\Leftrightarrow R(A) = R(\overline A ) = k < n\)
- Khi đó, hệ phương trình có k ẩn chính ứng với k phần tử dẫn đầu và n - k ẩn tự do, được chuyển sang vế phải.
- Hệ vô nghiệm \( \Leftrightarrow R(A) < R(\overline A )\)
Ví dụ: Giải hệ phương trình tuyến tính
\(\left\{ \begin{array}{l} {x_1} + {x_2} - {x_3} = 2\\ 2{x_1} + {x_3} = 1\\ {x_2} + 2{x_3} = - 2 \end{array} \right.\,(I)\)
Ma trận hệ số mở rộng của (I) là

Ta có: \(R(A) = R(\overline {A)} = 3\) số ẩn
Vậy hệ có nghiệm duy nhất: X = (1;0;-1)
Ví dụ: Giải hệ phuơng trình tuyến tính
\(\left\{ \begin{array}{l} {x_2} - 2{x_3} = 1\\ {x_1} + {x_3} = - 2\\ 2{x_1} + 2{x_2} - 2{x_3} = - 1 \end{array} \right.(I)\)
Giải: Ma trận hệ số mở rộng của (I) là
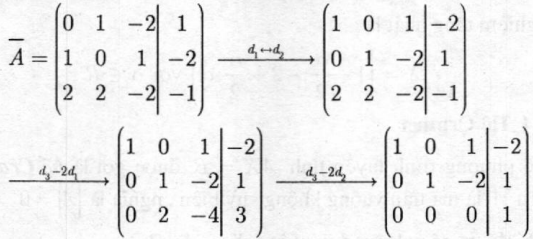
Ta có: \(R(A) = 2 < R(\overline {A)} = 3\). Vậy hệ vô nghiệm.
Ví dụ: Giải hệ phương trình tuyến tính
\(\left\{ \begin{array}{l} {x_1} - {x_2} + {x_3} = 3\\ 2{x_1} + {x_3} = 2\\ 3{x_1} - {x_2} + 2{x_3} = 5 \end{array} \right.\,(I)\)
Giải: Ma trận hệ số mở rộng của (I) là
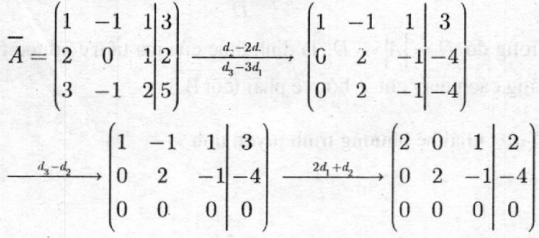
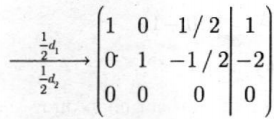
Ta có: \(R\left( A \right){\rm{ }} = {\rm{ }}R\left( {\overline A } \right){\rm{ }} = {\rm{ }}2\) (số ẩn là 3). Vậy hệ có vô số nghiệm với 2 ẩn chính ứng với 2 phần tử dẫn đầu là x1, x2. Giải x1, x2 theo ẩn tự do x3 ta có hệ phương trình có vô số nghiệm với nghiệm tổng quát là: \(X = \left( {1 - \frac{\alpha }{2}; - 2 + \frac{\alpha }{2};\alpha } \right)\,với\,\alpha \in R\)
4. Hệ Cramer
Hệ phương trình tuyến tính AX = B được gọi là hệ Cramer nếu A là ma trận vuông không suy biến , nghĩa là \(\left| A \right| \ne 0\)
Khi đó, ta có nghiệm duy nhất: \(X = A^{-1}B\)
Nếu cấp của ma trận A khá lớn thì việc tìm \(A^{-1}\) tương đổi phức tạp. Hơn nữa, có khi ta chi cần tìm một vài ẩn \(x_j\) thay vì toàn bộ các ẩ\(X=(x_1; x_2;....;x_n)\). Từ đó, người ta tìm ra công thúc tính từng ẩn \(x_j\) dựa vào công thức \(X = A^{-1}B\) như sau :
\({x_j} = \frac{{{D_j}}}{D}\)
Trong đó \(D = \left| A \right|\,và\,{D_j}\) là định thức của ma trận có được từ A bằng cách thay cột j bởi vế phải (cột B ).
Ví dụ: Giải hệ phương trình tuyến tính
\(\left\{ \begin{array}{l} {x_1} - 2{x_2} - {x_3} = - 3\\ - 3{x_1} + {x_2} = - 2\\ - 2{x_1} + {x_3} = 1 \end{array} \right.\)
Giải:
Ta có:
\(\begin{array}{l} D = \left| {\begin{array}{*{20}{c}} 1&{ - 2}&{ - 1}\\ { - 3}&1&0\\ { - 2}&0&1 \end{array}} \right| = - 7;\,\,\,\,{D_1} = \left| {\begin{array}{*{20}{c}} { - 3}&{ - 2}&{ - 1}\\ { - 2}&1&0\\ 1&0&1 \end{array}} \right| = - 6\\ {D_2} = \left| {\begin{array}{*{20}{c}} 1&{ - 3}&{ - 1}\\ { - 3}&{ - 2}&0\\ { - 2}&1&1 \end{array}} \right| = - 4;\,\,\,{D_3} = \left| {\begin{array}{*{20}{c}} 1&{ - 2}&{ - 3}\\ { - 3}&1&{ - 2}\\ { - 2}&0&1 \end{array}} \right| = - 19 \end{array}\)
Vậy nghiệm là \(X = \left( {\frac{{{D_1}}}{D};\frac{{{D_2}}}{D};\frac{{{D_3}}}{D}} \right) = \left( {\frac{6}{7};\frac{4}{7};\frac{{19}}{7}} \right)\)
5. Hệ phương trình tuyến tính thuần nhất.
Hệ phương trình tuyến tính AX = 0 gọi là hệ thuần nhất. Ngoài các tính chất chung của hệ AX = B, hệ thuần nhất AX = 0 còn có các tính chất riêng như sau :
- Hệ luôn luôn có nghiệm tầm thường X = 0 (không có trường hợp hệ vô nghiệm)
- Nếu A là ma trận vuông, không suy biến thì hệ có nghiệm duy nhất \(X = A^{-1}0 = 0\), chính là nghiệm tầm thường.
- Nếu hệ có vô số nghiệm thì tập nghiệm là một không gian con của không gian \(R^n\) (với n là số ẩn). Một cơ sở của không gian nghiệm được gọi là một hệ nghiệm cơ bản.
Ví dụ: Giải hệ phương trình tuyến tính \(\left\{ \begin{array}{l} {x_1} - {x_2} + {x_3} = 0\\ 2{x_1} - {x_2} = 0\\ {x_2} + 2{x_3} = 0 \end{array} \right.\)
Giải:
Ta có: \(D = \left| {\begin{array}{*{20}{c}} 1&{ - 1}&1\\ 2&{ - 1}&0\\ 0&1&2 \end{array}} \right| = 4 \ne 0\)
Đây là hệ Cramer, nên hệ có nghiệm duy nhất X = (0; 0; 0)
Ví dụ: Giải hệ phương trình tuyến tính \(\left\{ \begin{array}{l} {x_1} + 2{x_2} + 5{x_3} = 0\\ - 2{x_1} + {x_2} = 0\\ - {x_1} + 3{x_2} + 5{x_3} = 0 \end{array} \right.\)
Giải:
Ta có:
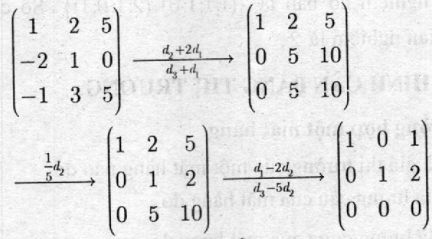
Hệ có vô số nghiệm với nghiệm tổng quát là: \(X = ( - \alpha ; - 2\alpha ;\alpha ) = \alpha ( - 1; - 2;1),\alpha \in R\)
Một hệ nghiệm cơ bản là {(-1;-2;1)}. Số chiều của không gian nghiệm là 1.
Ví dụ: Giải hệ phương trình tuyến tính
\(\left\{ \begin{array}{l} {x_1} - {x_2} - {x_4} = 0\\ {x_2} - {x_3} - {x_4} = 0\\ 2{x_1} - {x_2} - {x_3} - 3{x_4} = 0 \end{array} \right.\)
Giải:
Ta có:
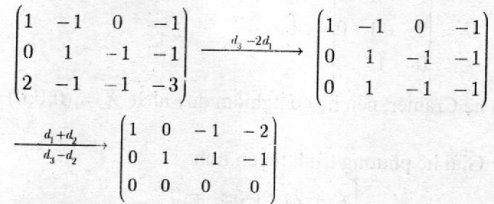
Nghiệm tổng quát là:
\(X = (\alpha + 2\beta ;\alpha + \beta ;\alpha ;\beta ) = \alpha (1;1;1;0) + \beta (2;1;0;1)\,với\,\,\alpha ,\beta \in R\)
Một hệ nghiệm cơ bản là {(1;1;1;0).(2;1;0;1)}. Số chiều của không gian nghiệm là 2.
Từ khóa » Hạng Của Ma Trận Mở Rộng
-
[PDF] Hạng Của Ma Trận & Hệ Phương Trình Tuyến Tính - TaiLieu.VN
-
Hạng (đại Số Tuyến Tính) – Wikipedia Tiếng Việt
-
Hạng Của Ma Trận Mở Rộng - 123doc
-
Hạng Của Ma Trận - YouTube
-
Các Dạng Toán Về Hạng Của Ma Trận Và Phương Pháp Giải - Vted
-
[DOC] Hạng Của Ma Trận Mở Rộng - 5pdf
-
[PDF] Bài Giảng Toán Cao Cấp PGS.TS Lê
-
[PDF] BÀI GIẢNG ĐAI SỐ TUYẾN TÍNH - FITA-VNUA
-
Top 9 Hạng Của Ma Trận Mở Rộng 2022 - Mua Trâu
-
Chương 2 - Ma Trận (tiếp Theo) | CTCT - Chúng Ta Cùng Tiến
-
[PDF] BÀI 5
-
[PDF] 4: Hạng Ma Trận
-
MA TRẬN MỞ RỘNG Tiếng Anh Là Gì - Trong Tiếng Anh Dịch - Tr-ex