Bài 1: Tìm Khoảng đơn điệu Của Hàm Số

• HOC247 KIDS
• TOÁN NÂNG CAO THCS
  • Chương trình Toán nâng cao THCS lớp 6
  • Chương trình Toán nâng cao THCS lớp 7
  • Chương trình Toán nâng cao THCS lớp 8
  • Chương trình Toán nâng cao THCS lớp 9
  • LỚP 10 CHUYÊN
• BỒI DƯỠNG HSG
  • Bồi dưỡng học sinh giỏi Quốc Gia
  • BM2E
• THPT QG 2022
  • Toán học
  • Vật lý
  • Hóa học
  • Sinh học
  • Ngữ văn
  • Tiếng Anh
  • Khoá H2 - Luyện thi THPT Quốc gia môn Toán
  • Khóa H2 - Luyện thi THPT Quốc gia môn Ngữ văn
  • Khóa H2 - Luyện thi THPT Quốc gia môn Tiếng Anh
  • Khoá H2 - Luyện thi THPT Quốc gia môn Vật Lý
  • Khóa H2 - Luyện thi THPT Quốc gia môn Hóa Học
  • Khoá H2 - Luyện thi THPT Quốc gia môn Sinh Học

• GIÁO VIÊN ĐỀ THI ONLINE
• Đăng nhập

Ra mắt HOC247 Kids nền tảng học tập Online #1 Hướng dẫn FAQ Hỗ trợ: 0973 686 401 KHÓA HỌC Nền tảng học Online#1 cho HS Tiểu Học Tải App

• CÁC KHÓA HỌC
• BM2E
• Luyện thi THPT QG 2018
• Toán học
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng Anh
• Toán nâng cao THCS
• Chương trình Toán NC THCS lớp 6
• Chương trình Toán NC THCS lớp 7
• Chương trình Toán NC THCS lớp 8
• Chương trình Toán NC THCS lớp 9
• Lớp 10 Chuyên
• Bồi dưỡng HSG
• Giáo viên
• Đề thi online

• ĐĂNG NHẬP
• Vui lòng nhập email!
• Vui lòng nhập mật khẩu!
• Tài khoản giảng viên.
• ĐĂNG NHẬP ĐĂNG KÝ

• ĐĂNG KÝ
• Vui lòng nhập email!
• Vui lòng nhập mật khẩu!
• Mật khẩu em nhập không khớp
• ĐĂNG KÝ

Trang Chủ » Khoá học: Khoá H2 - Luyện thi THPT Quốc gia môn Toán

Chuyên đề 1: Đạo hàm và ứng dụng

Bài 1: Tìm khoảng đơn điệu của hàm số Giáo viên: Thời lượng: 00:55:29 Bài tập: 10 bài

GIỚI THIỆU BÀI HỌC

Bài giảng sẽ giúp các em nắm được kiến thức cơ bản về cách tìm khoảng đơn điệu của hàm số như:

• Định nghĩa
• Điều kiện đủ để hàm số đơn điệu
• Các bước tìm khoảng đơn điệu của hàm số

NỘI DUNG BÀI HỌC

1. Định nghĩa Cho hàm số f(x) xác định trên (a;b) a) f(x) đồng biến trên (a;b) nếu \(\left\{\begin{matrix} x_1,x_2\in (a;b)\\ x_1<x_2 \end{matrix}\right.\Rightarrow f(x_1)<f(x_2)\) b) f(x) nghịch biến trên (a;b) nếu \(\left\{\begin{matrix} x_1,x_2\in (a;b)\\ x_1<x_2 \end{matrix}\right.\Rightarrow f(x_1)>f(x_2)\) 2. Điều kiện đủ để hàm số đơn điệu Cho hàm số f(x) xác định và liên tục trên (a;b) a) Nếu \(f'(x) >0 \forall x\in (a;b)\) thì f(x) đồng biến trên (a;b) Nếu \(f'(x) <0 \forall x\in (a;b)\) thì f(x) thì nghịch biến trên (a;b) b) Nếu \(f'(x)\geq 0\forall x\in (a;b)\) và f'(x) = 0 tại hữu hạn điểm thuộc (a;b) thì f(x) đồng biến trên (a;b) Nếu \(f'(x) \leqslant 0\forall x\in (a;b)\) và f'(x) = 0 tại hữu hạn điểm thuộc (a;b) thì f(x) nghịch biến trên (a;b) 3. Tìm khoảng đơn điệu của hàm số B1: Tìm TXĐ B2: Tính f'(x) Tìm nghiệm f'(x) = 0 B3: Dựa vào định lý ⇒ KL (Bảng biến thiên) Chú ý: 1) Dấu của f(x) = ax + b (\(a\neq 0\)) 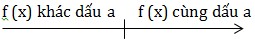2) Dấu của f(x) = ax2 + bx + c (\(a\neq 0\)) \(\Delta <0\) thì f(x) cùng dấu a 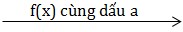\(\Delta =0\) thì f(x) cùng dấu với a 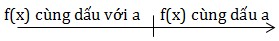\(\forall x\neq -\frac{b}{2a}(f(-\frac{b}{2a})=0)\) \(\Delta >0\) thì f(x) = 0 có 2 nghiệm \(x_1.x_2(x_1<x_2)\) 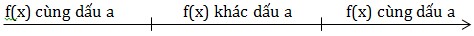Quy tắc: “Ngoài cùng trong khác” VD1: Tìm khoảng đơn điệu của hàm số \(f(x)=-x^3+3x^2\) Giải TXĐ: D = R \(f'(x)=-3x^2+3.2x\) \(=-3x(x-2)\) \(f'(x)=0\Leftrightarrow \begin{bmatrix} x=0\\ x=2 \end{matrix}\) 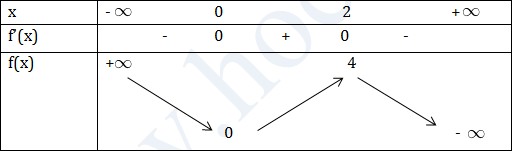Hàm số đồng biến trên (0;2) Hàm số nghịch biến trên các khoảng \((-\infty ;0);(2;+\infty)\) Chú ý: Hàm số đồng biến nghịch biến trên (a;b); (c;d) thì chưa chắc đồng biến (nghịch biến) ​trên \((a;b)\cup (c;d)\) VD2: Tìm khoảng đơn điệu của hàm số \(f(x)=x^3-3x^2+3x+2\) Giải TXĐ: D = R \(f'(x)=3x^2-6x+3\) \(=3(x^2-2x+1)\) \(=3(x-1)2\) \(f'(x)\geq 0 \ \forall x, f'(x)=0\Leftrightarrow (x-1)^2=0\Leftrightarrow x=1\) 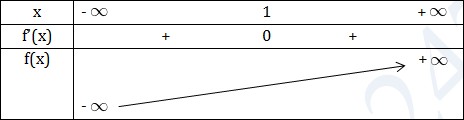Hàm số đồn biến trên R VD3: Tìm khoảng đơn điệu của hàm số \(f(x)=x^3+x^2+8x+6\) Giải TXĐ: D = R \(f'(x)=3x^2+2x+8>0 \ \forall x\in R\) Vì \(\left\{\begin{matrix} \Delta '=1-3.8=-23< 0\\ a=3>0 \end{matrix}\right.\) Kết luận: Hàm số đồng biến trên R 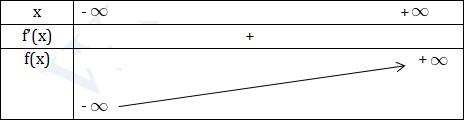VD4: Tìm khoảng đơn điệu của hàm số \(f(x)=x^4-2x^2\) Giải TXĐ: D = R \(f'(x)=4x^3-4x\) \(=4x(x^2-1)\) \(f'(x)=0\Leftrightarrow 4x(x^2-1)=0\Leftrightarrow \begin{bmatrix} x=0\\ x=1\\ x=-1 \end{matrix}\) 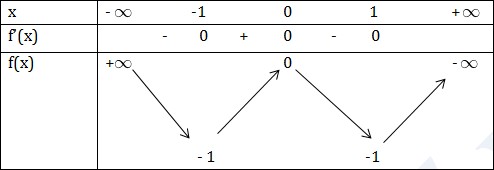KL: Hàm số đồng biến trên \((-1;0);(1;+\infty )\) Hàm số nghịch biến trên \((-\infty ;-1);(0;1 )\) VD5: Tìm khoảng đơn điệu của hàm số \(f(x)=\frac{8x+6}{2x-3}\) Giải TXĐ: \(D = R \setminus\left \{ \frac{3}{2} \right \}\) \(f'(x)=\frac{8(2x-3)-2(8x+6)}{(2x-3)^2}=\frac{-36}{(2x-3)^2}< 0\) KL: Hàm số nghịch biến \((-\infty ;\frac{3}{2}); (\frac{3}{2};+\infty )\) VD6: Tìm khoảng đơn điệu của hàm số \(f(x)=\sqrt{x-2}+\sqrt{4-x}\) Giải TXĐ: Hàm số xác định khi \(\left\{\begin{matrix} x-2\geqslant 0\\ 4-x\geq 0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geqslant 2\\ x\leqslant 4 \end{matrix}\right.\) D=[2;4] \(f'(x)=\frac{1}{2\sqrt{x-2}}-\frac{1}{2\sqrt{4-x}}\) \(f(x)=0\Rightarrow \sqrt{x-2}=\sqrt{4-x}\) \(\Rightarrow x-2=4-x\) \(\Rightarrow x=3\in [2;4]\) 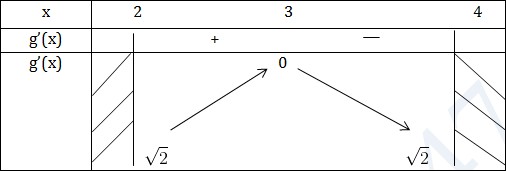Hàm số nghịch biến trên (3;4) Hàm số đồng biến trên (2;3)

HỎI ĐÁP PHẦN BÀI HỌC (5)

• Trần Thảo 21:33 ngày 19/08/2018 thầy dạy từ bài 6 vậy k có bài 1,2,3,4,5 ạ Thích Chưa trả lời
• Trần Thảo 20:13 ngày 19/08/2018 thầy giảng kĩ quá ^^ Thích Chưa trả lời
• Bin bin 10:43 ngày 04/01/2018 em khong hieu a Thích (1) 1 Trả lời
  • Trần Thảo 19:30 ngày 19/08/2018 bạn phải hỏi rõ là k hiểu chỗ nào chứ Thích (1)
• Ngô Tùng Dương 11:30 ngày 25/08/2017 ở ví dụ 5 tại sao khi tính lim trong bảng biến thiên lại ra 4 ạ Thích 1 Trả lời
  • Mod Toán Học 14:09 ngày 25/08/2017

    Đây là kiến thức tính cơ bản của chương trình Giải tích lớp 11 em nhé!

    \(\mathop {\lim }\limits_{x \to + \infty } \frac{{8x + 6}}{{2x - 3}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{8 + \frac{6}{x}}}{{2 - \frac{3}{x}}} = \frac{8}{2} = 4.\)

    Thích
• Trần Đình Đức 22:03 ngày 10/08/2017 e vẫn chưa rõ về chỗ " hàm số đồng biến trên khoảng (a,b) hàm số đồng biến trên khoảng (c,d) nhưng hàm số chưa chắc đã đồng biến trên khoảng hợp của hai khoảng đó " thầy có thể giải thích rõ hơn đc ko ạ Thích 1 Trả lời
  • Mod Toán Học 14:08 ngày 11/08/2017

    Chào Đức!

    Mod lấy một ví dụ minh họa cho em hiểu luôn nhé.

    Xét hàm số \(y = \frac{{x - 1}}{{x + 2}}\)

    TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\)

    \(y' = \frac{3}{{{{(x + 2)}^2}}} > 0,\forall x \in D\)

    Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\)

    Hàm số không đồng biến trên \(\left( { - \infty ; - 2} \right) \cup \left( { - 2; + \infty } \right),\) thật vậy:

    Với \({x_1} = - 3 \in \left( { - \infty ; - 2} \right) \cup \left( { - 2; + \infty } \right)\) ta có: \(f({x_1}) = 4.\)

    Với \({x_2} = 1 \in \left( { - \infty ; - 2} \right) \cup \left( { - 2; + \infty } \right)\) ta có: \(f({x_2}) = 0.\)

    Ta thấy \({x_1} < {x_2}\) nhưng \(f({x_1}) > f({x_2})\) suy ra hàm số không đồng biến trên \(\left( { - \infty ; - 2} \right) \cup \left( { - 2; + \infty } \right).\)

    Nên nhớ trong chương trình phổ thông mình chỉ xét tính đơn điệu trên một khoảng, đoạn, nửa khoảng, không xét trên các khoảng hợp em nhé.

    Chúc em học tốt!

    Thích

Miễn phí Đăng ký ngay

NỘI DUNG KHÓA HỌC

Đăng ký miễn phí

Học thử khóa H2 môn Toán năm 2018

Trải nghiệm miễn phí 8 bài học Chuyên đề 1: Đạo hàm và ứng dụng 1 00:55:29 Bài 1: Tìm khoảng đơn điệu của hàm số Hỏi đáp 10 Bài tập 2 00:28:42 Bài 2: Tìm tham số để hàm số đơn điệu trên một miền Hỏi đáp 10 Bài tập 3 Kiểm tra: Đề thi online Xác định khoảng đơn điệu của hàm số 0 Hỏi đáp 45 phút 20 Câu hỏi 100.000đ Đăng ký chuyên đề

Chuyên đề 1: Đạo hàm và ứng dụng

4 00:32:49 Bài 3: Ứng dụng tính đơn điệu giải phương trình Hỏi đáp 10 Bài tập 5 00:32:29 Bài 4: Ứng dụng tính đơn điệu giải bất phương trình Hỏi đáp 9 Bài tập 6 00:29:14 Bài 5: Ứng dụng tính đơn điệu giải hệ phương trình Hỏi đáp 6 Bài tập 7 00:43:58 Bài 6: Ứng dụng tính đơn điệu chứng minh bất đẳng thức Hỏi đáp 7 Bài tập 8 00:35:43 Bài 7: Bài toán tìm cực trị Hỏi đáp 10 Bài tập 9 00:24:57 Bài 8: Tìm tham số để hàm số đạt cực trị thỏa mãn điều kiện cho trước Hỏi đáp 15 Bài tập 10 00:22:45 Bài 9: Bài toán tìm GTLN, GTNN của hàm số Hỏi đáp 15 Bài tập 11 00:32:39 Bài 10: Tiệm cận Hỏi đáp 15 Bài tập 12 Kiểm tra: Đề thi online Tìm cực trị, GTLN, GTNN của hàm số 0 Hỏi đáp 45 phút 20 Câu hỏi 13 00:15:29 Bài 11: Ôn tập, nâng cao Hỏi đáp 10 Bài tập 14 Kiểm tra: Đề thi online chuyên đề Đạo hàm và ứng dụng 0 Hỏi đáp 90 phút 20 Câu hỏi 60.000đ Đăng ký chuyên đề

Chuyên đề 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số

15 00:31:52 Bài 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba Hỏi đáp 10 Bài tập 16 00:16:20 Bài 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn Hỏi đáp 10 Bài tập 17 00:20:18 Bài 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số phân thức b1/b1 Hỏi đáp 10 Bài tập 18 00:40:05 Bài 4: Bài toán viết phương trình tiếp tuyến Hỏi đáp 16 Bài tập 19 00:27:55 Bài 5: Bài toán tương giao giữa các đồ thị Hỏi đáp 10 Bài tập 20 01:30:04 Bài 6: Ôn tập, nâng cao Hỏi đáp 10 Bài tập 21 Kiểm tra: Đề thi online chuyên đề Khảo sát sự biến thiên và vẽ đồ thị hàm số 0 Hỏi đáp 90 phút 20 Câu hỏi 60.000đ Đăng ký chuyên đề

Chuyên đề 3: Khối đa diện

22 00:23:11 Bài 1: Khái niệm khối đa diện Hỏi đáp 10 Bài tập 23 00:33:36 Bài 2: Tính thể tích bằng cách trực tiếp Hỏi đáp 10 Bài tập 24 00:41:57 Bài 3: Tính thể tích bằng cách gián tiếp Hỏi đáp 10 Bài tập 25 00:34:15 Bài 4: Ứng dụng của thể tích tính khoảng cách, chứng minh hệ thức Hỏi đáp 10 Bài tập 26 00:41:18 Bài 5: Ôn tập, nâng cao Hỏi đáp 27 Kiểm tra: Đề thi online chuyên đề Khối đa diện 0 Hỏi đáp 90 phút 20 Câu hỏi 100.000đ Đăng ký chuyên đề

Chuyên đề 4: Khối tròn xoay

28 00:20:04 Bài 1: Mặt nón - hình nón - khối nón Hỏi đáp 10 Bài tập 29 00:31:25 Bài 2: Thể tích khối nón Hỏi đáp 10 Bài tập 30 00:19:03 Bài 3: Diện tích xung quanh, diện tích toàn phần hình nón Hỏi đáp 10 Bài tập 31 00:23:04 Bài 4: Mặt trụ - hình trụ - khối trụ Hỏi đáp 10 Bài tập 32 00:16:58 Bài 5: Thể tích khối trụ Hỏi đáp 10 Bài tập 33 00:27:18 Bài 6: Diện tích xung quanh, diện tích toàn phần hình trụ Hỏi đáp 10 Bài tập 34 00:58:51 Bài 7: Mặt cầu - hình cầu Hỏi đáp 10 Bài tập 35 00:21:56 Bài 8: Thể tích khối cầu Hỏi đáp 10 Bài tập 36 00:15:37 Bài 9: Diện tích mặt cầu Hỏi đáp 10 Bài tập 37 00:32:41 Bài 10: Ôn tập, nâng cao Hỏi đáp 10 Bài tập 38 Đề thi online chuyên đề Khối tròn xoay 0 Hỏi đáp 60 phút 20 Câu hỏi 140.000đ Đăng ký chuyên đề

Chuyên đề 5: Phương pháp tọa độ trong không gian

39 00:27:49 Bài 1: Tọa độ của vectơ trong không gian Hỏi đáp 5 Bài tập 40 00:40:44 Bài 2: Tọa độ của điểm trong không gian Hỏi đáp 5 Bài tập 41 00:21:18 Bài 3: Ứng dụng của tích vô hướng chứng minh quan hệ vuông góc, tính góc Hỏi đáp 5 Bài tập 42 00:19:56 Bài 4: Ứng dụng tích vô hướng giải phương trình, bất phương trình, hệ phương trình Hỏi đáp 6 Bài tập 43 00:28:49 Bài 5: Ứng dụng chứng minh bất đẳng thức, tìm cực trị Hỏi đáp 6 Bài tập 44 00:18:00 Bài 6: Ứng dụng tích có hướng chứng minh bốn điểm không đồng phẳng Hỏi đáp 5 Bài tập 45 00:18:23 Bài 7: Ứng dụng tích có hướng tính diện tích Hỏi đáp 3 Bài tập 46 00:22:03 Bài 8: Ứng dụng tích có hướng tính thể tích Hỏi đáp 5 Bài tập 47 Kiểm tra: Đề thi online phần Ứng dụng tích vô hướng, có hướng 0 Hỏi đáp 45 phút 20 Câu hỏi 48 00:32:07 Bài 9: Bài toán viết phương trình mặt phẳng Hỏi đáp 6 Bài tập 49 00:30:07 Bài 10: Bài toán về vị trí tương đối giữa các mặt phẳng Hỏi đáp 7 Bài tập 50 00:29:42 Bài 11: Bài toán khoảng cách từ điểm đến mặt phẳng Hỏi đáp 7 Bài tập 51 00:19:42 Bài 12: Bài toán góc giữa các mặt phẳng Hỏi đáp 6 Bài tập 52 00:37:37 Bài 13: Bài toán xác định điểm liên quan đến mặt phẳng Hỏi đáp 8 Bài tập 53 Kiểm tra: Đề thi online phần Mặt phẳng 0 Hỏi đáp 45 phút 20 Câu hỏi 54 00:30:03 Bài 14: Viết phương trình đường thẳng trong không gian Hỏi đáp 6 Bài tập 55 00:37:40 Bài 15: Bài toán về vị trí tương đối giữa các đường thẳng Hỏi đáp 6 Bài tập 56 00:36:12 Bài 16: Khoảng cách giữa hai đường thẳng, đường thẳng và mặt phẳng song song Hỏi đáp 5 Bài tập 57 00:14:57 Bài 17: Góc giữa hai đường thẳng Hỏi đáp 5 Bài tập 58 00:15:13 Bài 18: Góc giữa đường thẳng và mặt phẳng Hỏi đáp 5 Bài tập 59 00:28:24 Bài 19: Xác định tọa độ điểm liên quan đến đường thẳng Hỏi đáp 6 Bài tập 60 Kiểm tra: Đề thi online phần Đường thẳng 0 Hỏi đáp 45 phút 20 Câu hỏi 61 00:19:21 Bài 20: Bài toán viết phương trình mặt cầu Hỏi đáp 6 Bài tập 62 00:16:08 Bài 21: Bài toán về vị trí tương đối giữa mặt cầu và mặt phẳng Hỏi đáp 5 Bài tập 63 00:31:38 Bài 22: Bài toán về vị trí tương đối giữa mặt cầu và đường thẳng Hỏi đáp 6 Bài tập 64 00:26:28 Bài 23: Xác định tọa độ điểm liên quan đến mặt cầu Hỏi đáp 5 Bài tập 65 Kiểm tra: Đề thi online phần Mặt cầu 0 Hỏi đáp 45 phút 20 Câu hỏi 66 00:37:14 Bài 24: Ôn tập, nâng cao Hỏi đáp 67 Kiểm tra: Đề thi online chuyên đề Phương pháp tọa độ trong không gian 0 Hỏi đáp 45 phút 20 Câu hỏi 70.000đ Đăng ký chuyên đề

Chuyên đề 6: Phương trình, bất phương trình mũ

68 00:21:04 Bài 1: Lũy thừa Hỏi đáp 5 Bài tập 69 00:10:51 Bài 2: Phương trình mũ - Phương pháp đưa về cùng cơ số Hỏi đáp 5 Bài tập 70 00:20:48 Bài 3: Phương trình mũ - Phương pháp logarit hóa Hỏi đáp 5 Bài tập 71 00:26:50 Bài 4: Phương trình mũ - Phương pháp đặt ẩn phụ Hỏi đáp 8 Bài tập 72 00:19:10 Bài 5: Phương trình mũ - Phương pháp hàm số Hỏi đáp 5 Bài tập 73 Kiểm tra: Đề thi online Phương trình mũ 0 Hỏi đáp 45 phút 20 Câu hỏi 74 00:13:30 Bài 6: Bất phương trình mũ - Phương pháp đưa về cùng cơ số Hỏi đáp 6 Bài tập 75 00:13:05 Bài 7: Bất phương trình mũ - Phương pháp logarit hóa Hỏi đáp 5 Bài tập 76 00:24:27 Bài 8: Bất phương trình mũ - Phương pháp đặt ẩn phụ Hỏi đáp 5 Bài tập 77 00:16:40 Bài 9: Bất phương trình mũ - Phương pháp hàm số Hỏi đáp 5 Bài tập 78 Kiểm tra: Đề thi online Bất phương trình mũ 0 Hỏi đáp 45 phút 20 Câu hỏi 79 00:35:27 Bài 10: Ôn tập, nâng cao Hỏi đáp 80 Kiểm tra: Đề thi online chuyên đề Phương trình, bất phương trình mũ 0 Hỏi đáp 45 phút 20 Câu hỏi 70.000đ Đăng ký chuyên đề

Chuyên đề 7: Phương trình, bất phương trình logarit

81 00:21:11 Bài 1: Logarit Hỏi đáp 5 Bài tập 82 00:23:32 Bài 2: Phương trình logarit - Phương pháp đưa về cùng cơ số Hỏi đáp 5 Bài tập 83 00:10:13 Bài 3: Phương trình logarit - Phương pháp mũ hóa Hỏi đáp 6 Bài tập 84 00:24:59 Bài 4: Phương trình logarit - Phương pháp đặt ẩn phụ Hỏi đáp 5 Bài tập 85 00:24:57 Bài 5: Phương trình logarit - Phương pháp hàm số Hỏi đáp 5 Bài tập 86 Kiểm tra: Đề thi online Phương trình logarit 0 Hỏi đáp 45 phút 87 00:15:21 Bài 6: Bất phương trình logarit - Phương pháp đưa về cùng cơ số Hỏi đáp 5 Bài tập 88 00:19:56 Bài 7: Bất phương trình logarit - Phương pháp mũ hóa Hỏi đáp 9 Bài tập 89 00:19:26 Bài 8: Bất phương trình logarit - Phương pháp đặt ẩn phụ Hỏi đáp 6 Bài tập 90 00:19:07 Bài 9: Bất phương trình logarit - Phương pháp hàm số Hỏi đáp 5 Bài tập 91 Kiểm tra: Đề thi online Bất phương trình logarit 0 Hỏi đáp 45 phút 20 Câu hỏi 92 00:24:37 Bài 10: Ôn tập, nâng cao Hỏi đáp 93 Kiểm tra: Đề thi online chuyên đề Phương trình logarit, bất phương trình lograit 0 Hỏi đáp 45 phút 20 Câu hỏi 70.000đ Đăng ký chuyên đề

Chuyên đề 8: Nguyên hàm, tích phân và ứng dụng

94 00:23:07 Bài 1: Nguyên hàm - Phương pháp biến đổi về nguyên hàm cơ bản Hỏi đáp 10 Bài tập 95 00:13:50 Bài 2: Nguyên hàm - Phương pháp đổi biến Hỏi đáp 10 Bài tập 96 00:15:03 Bài 3: Nguyên hàm - Phương pháp nguyên hàm từng phần Hỏi đáp 10 Bài tập 97 Kiểm tra: Đề thi online phần Nguyên hàm 0 Hỏi đáp 45 phút 20 Câu hỏi 98 00:23:24 Bài 4: Tích phân - Phương pháp biến đổi về tích phân cơ bản Hỏi đáp 10 Bài tập 99 00:15:59 Bài 5: Tích phân - Phương pháp đổi biến Hỏi đáp 10 Bài tập 100 00:17:53 Bài 6: Tích phân - Phương pháp tích phân từng phần Hỏi đáp 10 Bài tập 101 Kiểm tra: Đề thi online phần Tích phân 0 Hỏi đáp 45 phút 20 Câu hỏi 102 00:22:31 Bài 7: Ứng dụng của tích phân - Tính diện tích Hỏi đáp 10 Bài tập 103 00:26:30 Bài 8: Ứng dụng của tích phân - Tính thể tích Hỏi đáp 10 Bài tập 104 Kiểm tra: Đề thi online phần Ứng dụng của tích phân 0 Hỏi đáp 45 phút 20 Câu hỏi 105 00:20:44 Bài 9: Ôn tập, nâng cao Hỏi đáp 10 Bài tập 106 Kiểm tra: Đề thi online chuyên đề Nguyên hàm, Tích phân và Ứng dụng 0 Hỏi đáp 90 phút 30.000đ Đăng ký chuyên đề

Chuyên đề 9: Số phức

107 00:18:56 Bài 1: Các khái niệm cơ bản Hỏi đáp 10 Bài tập 108 00:16:15 Bài 2: Phép toán với số phức Hỏi đáp 10 Bài tập 109 00:25:32 Bài 3: Giải phương trình Hỏi đáp 10 Bài tập 110 00:21:41 Bài 4: Ôn tập, nâng cao Hỏi đáp 10 Bài tập 111 Kiểm tra: Đề thi online chuyên đề Số phức 0 Hỏi đáp 45 phút 20 Câu hỏi 140.000đ Đăng ký chuyên đề

Chuyên đề 10: Ôn tập chương trình Toán lớp 11

Giáo viên: TS.Phạm Sỹ Nam 112 Bài học 1 Hỏi đáp 113 Bài học 2 Hỏi đáp 114 Bài học 3 Hỏi đáp 115 Bài học 4 Hỏi đáp 116 Bài học 5 Hỏi đáp ×

THÔNG BÁO

Lời đầu tiên, HOC247 xin cảm ơn các em học sinh đã tin tưởng và đồng hành cùng website hoc247.vn trong suốt thời gian vừa qua.

Vì mong muốn tạo điều kiện cho các em học sinh trên cả nước có thể tham gia học tập Online hoàn toàn miễn phí nên HOC247 chuyển toàn bộ các khoá học thu phí trên webiste hoc247.vn sang App HOC247 học miễn phí trên nền tảng iOS và Android.

Các em hãy cài đặt ngay App HOC247 để học tập hoàn toàn miễn phí các khoá học và luyện tập thư viện đề thi trắc nghiệm THPT QG.

ĐĂNG KÝ NHẬN EMAIL ĐĂNG KÝ EMAIL nhận thông tin bài giảng video, đề thi và ưu đãi đặc biệt từ HỌC247 Đăng ký ngay

• VỀ HỌC247
  • Giới thiệu
  • Liên hệ
  • Đối tác phân phối
  • Thỏa thuận sử dụng
  • Chính sách bảo mật
• TRỢ GIÚP
  • Hướng dẫn sử dụng
  • Câu hỏi thường gặp
  • Hotline: 0973 686 401
  • Thứ 2 - thứ 7: từ 08h30 - 21h00
  • Email: [email protected]
• KẾT NỐI MXH
  • Facebook
  • Youtube
• PHƯƠNG THỨC NẠP TIỀN
  • Hướng dẫn nạp tiền
  • Nạp tiền qua thẻ ATM, Visa, Master
  • Nạp tiền qua chuyển khoản ngân hàng

Copyright © 2022 Hoc247.vn Đơn vị chủ quản: Công Ty Cổ Phần Giáo Dục HỌC 247 GPKD: 0313983319 cấp ngày 26/08/2016 tại Sở Kế Hoạch và Đầu Tư TP.Hồ Chí Minh Giấy phép Mạng Xã Hội số: 638/GP-BTTTT cấp ngày 29/12/2020 Địa chỉ: P401, 54A Nơ Trang Long, Phường 14, Quận Bình Thạnh, TP. HCM, Việt Nam. Chịu trách nhiệm nội dung: Nguyễn Công Hà - Giám đốc Công ty CP Giáo Dục Học 247

Copyright © 2022 Hoc247.vn

Hotline: 0973 686 401 /Email: [email protected]

Chịu trách nhiệm nội dung: Nguyễn Công Hà - Giám đốc Công ty CP Giáo Dục Học 247