Bài 10 Trang 51 SGK Đại Số 10 | SGK Toán Lớp 10

Có thể bạn quan tâm

LG a

\(y = x^2– 2x – 1\)

Phương pháp giải:

Sử dụng các bảng biến thiên của hàm số bậc hai và đồ thị của hàm số trong các trường hợp \(a<0\) và \(a>0\). Xem tại đây.

Lời giải chi tiết:

Hàm số y = x2 – 2x – 1 có a = 1 > 0 ; b = –2 ; c = –1;

\(\Delta = {\left( { - 2} \right)^2} - 4.1.\left( { - 1} \right) = 8\)

+ Tập xác định D = R.

\(\begin{array}{l} - \frac{b}{{2a}} = - \frac{{ - 2}}{{2.1}} = 1\\ - \frac{\Delta }{{4a}} = - \frac{8}{{4.1}}= - 2\end{array}\)

+ Hàm số nghịch biến trên (–∞ ; 1) ; đồng biến trên (1 ; + ∞).

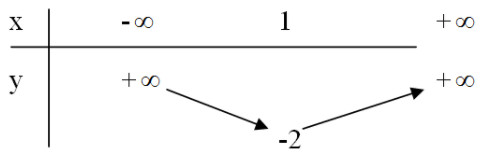
Bảng biến thiên

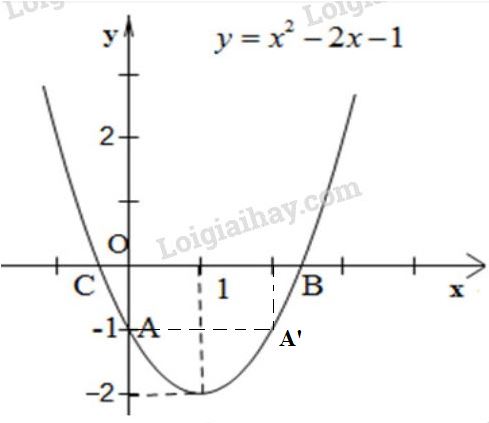
Đồ thị hàm số

Đồ thị là parabol có bề lõm hướng lên trên.

+ Đỉnh \(I(1; -2)\) với trục đối xứng \(x = 1\)

+ Giao điểm với trục tung là \(A(0;-1)\)

+ Điểm đối xứng với A qua đường thẳng x = 1 là A'(2 ; –1).

+ Giao điểm với trục hoành \(C (1-\sqrt2; 0)\) và \(B((1+\sqrt2; 0)\)