Bài 2.1, 2.2, 2.3 Phần Bài Tập Bổ Sung Trang 154 SBT Toán 7 Tập 1

Trang chủ » Bài Ii.2 Trang 154 Sbt Toán 7 » Bài 2.1, 2.2, 2.3 Phần Bài Tập Bổ Sung Trang 154 SBT Toán 7 Tập 1

Có thể bạn quan tâm

Bài II.1

Trên hình bs 6 , có bao nhiêu cặp tam giác bằng nhau ?

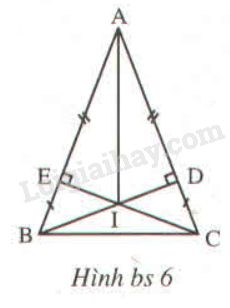
(A) \(2\);          (B) \(3\);         (C) \(4\)       (D) \(5\);

Hãy chọn đáp án đúng. 

Phương pháp giải:

Áp dụng các trường hợp bằng nhau của tam giác thường và tam giác vuông.

Lời giải chi tiết:

Xét hai tam giác vuông \(AEI\) và \(ADI\) có:

\(AI\) chung

\(AE=AD\) (gt)

\(\widehat {AEI} = \widehat {ADI} = {90^o}\)

\( \Rightarrow ΔAEI = ΔADI\) (cạnh huyền - cạnh góc vuông).

\( \Rightarrow EI=DI\) (hai cạnh tương ứng).

Xét hai tam giác vuông \(BEI\) và \(CDI\) có:

\(\widehat {BEI} = \widehat {CDI} = {90^o}\)

\(EI=DI\) (chứng minh trên)

\(BE=CD\) (gt)

\( \Rightarrow  ΔBEI = ΔCDI\) (c.g.c)

\( \Rightarrow  BI =CI\) (hai cạnh tương ứng).

\(AE=AD\) (gt)

\(BE=CD\) (gt)

\( \Rightarrow  AE+BE=AD+CD\)

\( \Rightarrow  AB=AC\).

Xét \(ΔAIB \) và \( ΔAIC\) có:

\(AB=AC\) (chứng minh trên)

\(BI=CI\) (chứng minh trên)

\(AI\) cạnh chung

\( \Rightarrow  ΔAIB = ΔAIC\) (c.c.c)

Xét \(ΔABD\) và \(ΔACE\) có:

\(AB=AC\) (chứng minh trên)

\(AD=AE\) (gt)

\(\widehat A\) chung

\( \Rightarrow  ΔABD = ΔACE\) (c.g.c)

\( \Rightarrow BD=CE\) (hai cạnh tương ứng).

Xét \(ΔBEC\) và \(ΔCDB\) có:

\(CE=BD\) (chứng minh trên)

\(BC \) chung

\(BE = CD\) (gt)

\( \Rightarrow ΔBEC = ΔCDB\) (c.c.c).

Vậy có \(5\) cặp tam giác bằng nhau.

Chọn D. 

Từ khóa » Bài Ii.2 Trang 154 Sbt Toán 7