Bài 2. Giá Trị Lượng Giác Của Một Cung - SureTEST
Có thể bạn quan tâm
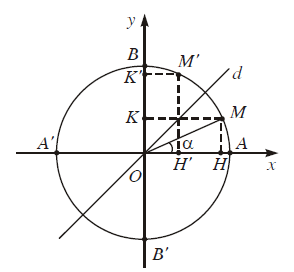
I. Giá trị của cung $\alpha $
1. Định nghĩa
Các giá trị sin$\alpha $, cos$\alpha $, tan$\alpha $, cot$\alpha $ được gọi là giá trị lượng giác của cung $\alpha $.
Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin.
2. Hệ quả
Bảng xác định dấu của các giá trị lượng giác

3. Giá trị lượng giác của các cung đặc biệt

II. Ý nghĩa hình học của tan và cot
1. Ý nghĩa hình học của tan$\alpha $
tan$\alpha $ được biểu diễn bởi độ dài đại số của vectơ $\overrightarrow {AT} $ trên trục t’At.
Trục t’At được gọi là trục tan.

2. Ý nghĩa hình học của cot$\alpha $
cot$\alpha $ được biểu diễn bởi độ dài đại số của vectơ $\overrightarrow {BS} $ trên trục s’Bs. Trục s’Bs được gọi là trục cot.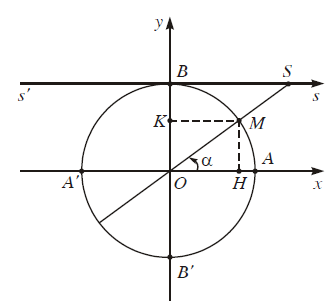
III. Quan hệ giữa các giá trị lượng giác
1. Công thức lượng giác cơ bản
$\begin{gathered} {\sin ^2}\alpha + {\cos ^2}\alpha = 1 \hfill \\ 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }},\alpha \ne \frac{\pi }{2} + k\pi ,k \in Z \hfill \\ 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }},\alpha \ne k\pi ,k \in Z \hfill \\ \tan \alpha .\cot \alpha = 1,\alpha \ne \frac{{k\pi }}{2},k \in Z \hfill \\ \end{gathered} $
2. Giá trị lượng giác của các cung có liên quan đặc biệt
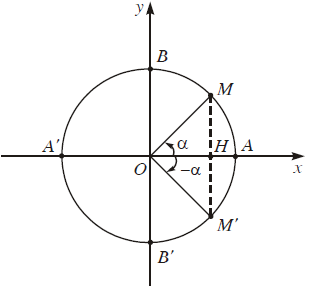
a) Cung đối nhau $\alpha $ và -$\alpha $
cos(-$\alpha $) = cos$\alpha $
sin(-$\alpha $) = -sin$\alpha $
tan(-$\alpha $) = -tan$\alpha $
cot(-$\alpha $) = -cot$\alpha $
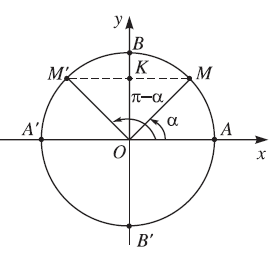
b) Cung bù nhau $\alpha $ và $\left( {\pi - \alpha } \right)$
$\begin{gathered} \sin \left( {\pi - \alpha } \right) = \sin \alpha \hfill \\ \cos \left( {\pi - \alpha } \right) = - \cos \alpha \hfill \\ \tan \left( {\pi - \alpha } \right) = - \tan \alpha \hfill \\ \cot \left( {\pi - \alpha } \right) = - \cot \alpha \hfill \\ \end{gathered} $
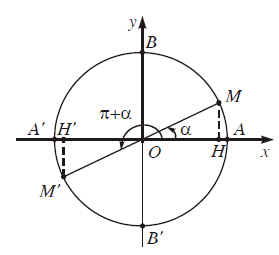
c) Cung hơn kém $\pi $: $\alpha $ và $\left( {\alpha + \pi } \right)$
$\begin{gathered} \sin \left( {\alpha + \pi } \right) = - \sin \alpha \hfill \\ \cos \left( {\alpha + \pi } \right) = - \cos \alpha \hfill \\ \tan \left( {\alpha + \pi } \right) = \tan \alpha \hfill \\ \cot \left( {\alpha + \pi } \right) = \cot \alpha \hfill \\ \end{gathered} $
d) Cung phụ nhau: $\alpha $ và $\left( {\frac{\pi }{2} - \alpha } \right)$
$\begin{gathered} \sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \hfill \\ \cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \hfill \\ \tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \hfill \\ \cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \hfill \\ \end{gathered} $
Từ khóa » Trục Tan X
-
Đường Tròn Lượng Giác - Tỷ Mỷ Làm Toán. Độc Lập Suy Nghĩ.
-
Vòng Tròn Lượng Giác Cơ Bản Và Hướng Dẫn Sử Dụng Chi Tiết
-
Đường Tròn Lượng Giác Lớp 11-Những Kiến Thức Cơ Bản Không Thể ...
-
[ Đường Tròn Lượng Giác ] Những Thông Tin Và Một Số Lưu ý Khi Dùng
-
Đường Tròn Lượng Giác - Một Số Kết Quả Cần Nhớ
-
Giá Trị Lượng Giác Của Góc (cung) Lượng Giác - Baitap123
-
Vòng Tròn Lượng Giác
-
Phương Trình Lượng Giác Cơ Bản Và Cách Giải - Toán Thầy Định
-
Hàm Lượng Giác – Wikipedia Tiếng Việt
-
Phương Pháp Đường Tròn Lượng Giác Vật Lý 12 - Kiến Guru
-
Phương Pháp Giải Bài Tập Toán 11 – Phần Hàm Số Lượng Giác
-
Tìm Các Giao Điểm Với Trục X Và Trục Y Y=tan(x) | Mathway
-
Bài 1: Hàm Số Lượng Giác - Hoc24