Bài 2. Hai đường Thẳng Vuông Góc - SureTEST
Có thể bạn quan tâm
I. Tích vô hướng của hai vectơ trong không gian
1. Góc giữa hai vectơ trong không gian
Trong không gian, cho $\overrightarrow u $ và $\overrightarrow v $ là hai vectơ – không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho $\overrightarrow {AB} = \overrightarrow u ,\overrightarrow {AC} = \overrightarrow v $. Khi đó ta gọi góc $\widehat {BAC}\left( {{0^o} \le \widehat {BAC} \le {{180}^o}} \right)$ là góc giữa hai vectơ $\overrightarrow u $ và $\overrightarrow v $ trong không gian, kí hiệu là $\left( {\overrightarrow u ,\overrightarrow v } \right)$.
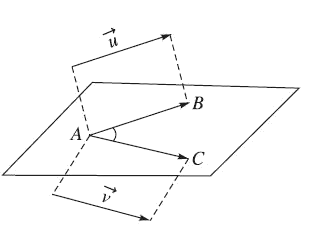
2. Tích vô hướng của hai vectơ trong không gian
Trong không gian, cho $\overrightarrow u $ và $\overrightarrow v $ là hai vectơ – không. Tích vô hướng của hai vectơ $\overrightarrow u $ và $\overrightarrow v $ là một số, kí hiệu là $\overrightarrow u .\overrightarrow v $, được xác định bởi công thức:
$\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.\cos \left( {\overrightarrow u .\overrightarrow v } \right)$
II. Vectơ chỉ phương của đường thẳng
Vectơ $\overrightarrow a $ là vectơ – không được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ $\overrightarrow a $ song song hoặc trùng với đường thẳng d.

* Nhận xét:
a) Nếu $\overrightarrow a $ là vectơ chỉ phương của đường thẳng d thì vectơ $k\overrightarrow a $ với $k \ne 0$ cũng là vectơ chỉ phương của d.
b) Một đường thẳng d trong không gian hoàn toàn được xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương $\overrightarrow a $ của nó.
c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vectơ chỉ phương cùng phương.
III. Góc giữa hai đường thẳng trong không gian
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.
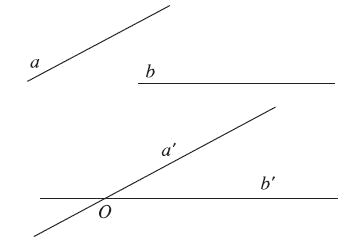
* Nhận xét:
a) Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.
b) Nếu $\overrightarrow u $ là vectơ chỉ phương của đường thẳng a và $\overrightarrow v $ là vectơ chỉ phương của đường thẳng b và $\left( {\overrightarrow u .\overrightarrow v } \right) = \alpha $ thì góc giữa hai đường thẳng a và b bằng $\alpha $ nếu ${0^o} \le \alpha \le {90^o}$ và bằng ${180^o} - \alpha $ nếu ${90^o} \le \alpha \le {180^o}$. Nếu a và b song song hoặc trùng nhau thì góc giữa chúng bằng ${0^o}$.
IV. Hai đường thẳng vuông góc
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng ${90^o}$.
Người ta kí hiệu hai đường thẳng a và b vuông góc với nhau là $a \bot b$.
* Nhận xét:
a) Nếu $\overrightarrow u $ và $\overrightarrow v $ lần lượt là các vectơ chỉ phương của hai đường thẳng a và b thì $a \bot b \Leftrightarrow \overrightarrow u .\overrightarrow v = 0$.
b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.Từ khóa » Tính Vecto U.v
-
Công Thức Tính Tích Vô Hướng Của Hai Vecto Trong Không Gian Cực Hay
-
Tích Vô Hướng, Tích Có Hướng Của Hai Vectơ - Ứng Dụng
-
Cho Vecto U=i+3j Và Vecto V=(2;-1) . Tính Vecto U.v - Hoc24
-
Lý Thuyết Tích Vô Hướng Của Hai Vectơ | SGK Toán Lớp 10
-
Công Thức Tính độ Dài Véc Tơ ( Overrightarrow U = ( (a;b;c) ) )
-
Xác định Tọa độ điểm, Vectơ Liên Quan đến Biểu Thức Dạng U + V, U
-
Cách để Tìm Góc Giữa Hai Véc Tơ - WikiHow
-
Cách Tính độ Dài Vecto
-
Cho Vecto U, V. Tính Tọa độ Của Các Vecto U + V, U - 1, 3u - 4v
-
Trong Không Gian Oxyz Cho Hai Vectơ U, Vecto V...
-
Công Thức Tính Góc Giữa 2 Vectơ Trong Mặt Phẳng Và Trong Không Gian
-
[PDF] Phƣơng Pháp Tọa độ Trong Không Gian
-
Tích Vô Hướng Của Hai Vectơ - Công Thức Học Tập
-
Tích Vô Hướng Của Hai Vecto, Trắc Nghiệm Toán Học Lớp 10 - Baitap123