Bài 2 - Lực Hấp Dẫn – Trọng Lực | Vật Lý Đại Cương
Có thể bạn quan tâm
Hai chất điểm bất kì luôn hút nhau một lực gọi là lực hấp dẫn. Lực này tỉ lệ thuận với tích khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
\( {{F}_{hd}}=G\frac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}} \) hay \( {{\overrightarrow{F}}_{hd}}=-G\frac{{{m}_{1}}{{m}_{2}}}{{{r}^{3}}}\vec{r} \) (2.8)
G: gọi là hằng số hấp dẫn, \( G=6,{{68.10}^{-11}}\text{ }\left( N{{m}^{2}}/k{{g}^{2}} \right) \)
Để tính lực hấp dẫn của một vật thể khối lượng m1 bất kì lên một chất điểm khối lượng m2, ta chia nhỏ vật thể đó thành những phần tử khối lượng dm1 rồi vận dụng (2.8), tích phân trên miền thể tích (V) của vật m1:
\( {{F}_{hd}}=G{{m}_{2}}\int\limits_{(V)}{\frac{d{{m}_{1}}}{{{r}^{2}}}} \) (2.9)
Kết quả tính tích phân (2.9) cho phép rút ra một số kết luận sau:
+ Lực hấp dẫn của một quả cầu đồng nhất lên một chất điểm ở ngoài quả cầu tựa hồ như toàn bộ khối lượng của quả cầu tập trung tại tâm của nó.
+ Lực hấp dẫn của một quả cầu rỗng đồng nhất lên một chất điểm ở trong quả cầu luôn bằng không. Nói cách khác, vỏ cầu đồng nhất không hấp dẫn bất kì vật nào bên trong nó.
Từ kết quả trên suy ra, lực hấp dẫn của Trái Đất tác dụng lên một vật nhỏ ở ngoài Trái Đất là:
\( {{F}_{hd}}=G\frac{mM}{{{\left( R+h \right)}^{2}}} \) (2.10)
Với M là khối lượng và R là bán kính của Trái Đất, h là độ cao từ mặt đất đến vật.
Nếu vật nằm trong lòng Trái Đất thì chỉ có phần nằm trong khối cầu bán kính r (r < R) là tác dụng lực hấp dẫn lên vật, do đó lực hấp dẫn trong trường hợp này là: \( {{F}_{hd}}=G\frac{mM’}{{{r}^{2}}} \), với M’ là khối lượng phần Trái Đất nằm trong hình cầu bán kính r. Coi mật độ khối lượng Trái Đất phân bố đều thì ta có:
\( \frac{M’}{V’}=\frac{M}{V}\Rightarrow M’=M\frac{V’}{V}=M\frac{{{r}^{3}}}{{{R}^{3}}} \) \( \Rightarrow {{F}_{hd}}=G\frac{Mm}{{{R}^{3}}}.r \) (2.11)
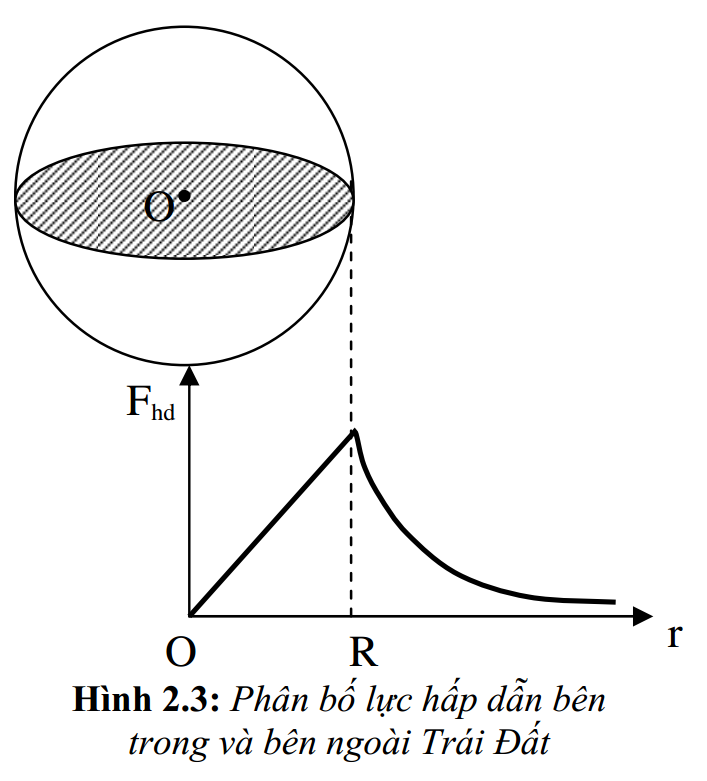
Vậy trong lòng Trái Đất, lực hấp dẫn tỉ lệ thuận với bán kính r; tại tâm Trái Đất, lực hấp dẫn triệt tiêu; tại bề mặt Trái Đất, lực hấp dẫn đạt cực đại; bên ngoài Trái Đất, lực hấp dẫn tỉ lệ nghịch với bình phương khoảng cách từ tâm Trái Đất đến vật. Hình (2.3) biểu diễn phân bố lực hấp dẫn của Trái Đất lên một vật nhỏ theo khoảng cách từ tâm Trái Đất đến vật.
Trong trường hợp tổng quát, tích phân (2.9) khá phức tạp, nên ta có thể tính gần đúng lực hấp dẫn giữa các vật thể bằng cách coi chúng là những chất điểm đặt tại khối tâm của chúng.

Bảng 2.1 Lực hấp dẫn của các vật trong vũ trụ
Do trị số của G quá nhỏ nên lực hấp dẫn chỉ đáng kể đối với vật có khối lượng rất lớn (các thiên thể). Chính vì thế, trong cuộc sống, ta không phát hiện ra lực hấp dẫn của các vật xung quanh. Bảng 2.1 cho ta một số giá trị của lực hấp dẫn giữa các vật khác nhau.
Từ khóa » Trọng Lượng Và Lực Hấp Dẫn
-
Lý Thuyết Lực Hấp Dẫn Và Trọng Lượng KHTN 6 Chân Trời Sáng Tạo
-
Lý Thuyết Trọng Lượng, Lực Hấp Dẫn KHTN 6 Kết Nối Tri Thức Với Cuộc ...
-
Lực Hấp Dẫn Là Gì? Trọng Lực Là Gì?
-
Trọng Lực Là Gì? Lực Hấp Dẫn Là Gì? - Công Thức Tính, đơn Vị đo
-
Trọng Lực, Lực Hấp Dẫn Và Những điều Chúng Ta Vẫn Lầm Tưởng
-
Bài 43: Trọng Lượng Lực Hấp Dẫn - KHTN Lớp 6 [Kết Nối Tri Thức]
-
Tương Tác Hấp Dẫn – Wikipedia Tiếng Việt
-
Lý Thuyết Lực Hấp Dẫn Và Trọng Lượng KHTN 6 Chân Trời Sáng Tạo
-
Lý Thuyết Lực Hấp Dẫn KHTN 6 Cánh Diều - Blog
-
Trọng Lực, Lực Hấp Dẫn Và Những điều Chúng Ta Vẫn Lầm Tưởng - Genk
-
Giải Bài 37: Lực Hấp Dẫn Và Trọng Lượng - Ibaitap
-
Sự Khác Biệt Giữa Trọng Lực Và Trọng Lượng - Sawakinome
-
Khoa Học Tự Nhiên 6 - Bài 43 - Trọng Lượng, Lực Hấp Dẫn - Kết Nối
-
Công Thức Xác định Lực Hấp Dẫn.