Bài 3. Nhị Thức Niu - Tơn - SureTEST

Trang chủ » Công Thức Khai Triển Niu Tơn » Bài 3. Nhị Thức Niu - Tơn - SureTEST

Có thể bạn quan tâm

SureLRN THÔNG BÁO Bạn có 0 thông báo mới Đang tải thông báo ...
Xem tất cả
  1. Trang chủ
  2. Củng cố kiến thức
  3. Lớp 11
  4. Toán

Bài 3. Nhị thức Niu - Tơn

I. Công thức nhị thức Newton

1. Khi khai triển nhị thức ${\left( {a + b} \right)^n}$, ta được công thức:

$\begin{array}{l} {\left( {a + b} \right)^n} = C_n^0{a^n} + C_n^1{a^{n - 1}}b + ... + C_n^{n - 1}a{b^{n - 1}} + C_n^n{b^n}\\ = C_n^0{b^n} + C_n^1{b^{n - 1}}a + ... + C_n^{n - 1}a{b^{n - 1}} + C_n^n{a^n} \end{array}$ (1)

(công thức Nhị thức Newton)

2. Trong vế phải của công thức (1) ta có:

a) Số hạng tử là n + 1;

b) Số hạng (hạng tử) thứ k + 1 là $C_n^k{a^{n - k}}{b^k},k = 0,1,...n$ (quy ước ${a^o} = 1,a \ne 0$).

c) Số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n.

d) Các hạng tử cách đều hạng tử đầu và hạng cuối có hệ số bằng nhau.

II. Tam giác Pascal

Trong công thức nhị thức Newton, cho n=0,1... và xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pascal.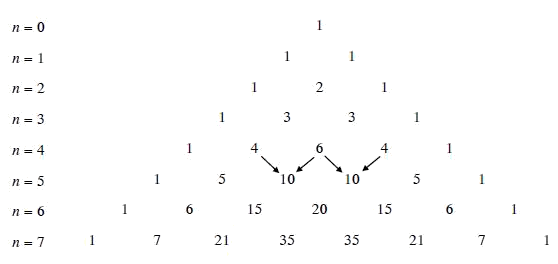

* Nhận xét:

Từ công thức $C_n^k = C_{n - 1}^{k - 1} + C_{n - 1}^k$ suy ra cách tính các số ở mỗi dòng dựa vào các số ở dòng trước nó. Chẳng hạn: $C_5^2 = C_4^1 + C_4^2 = 4 + 6 = 20$. Bài tập

Bạn chưa đăng nhập !

Vui lòng đăng nhập trước khi thực hiện thao tác này.

Đăng nhập Quay lại Đồng ý Đóng

Từ khóa » Công Thức Khai Triển Niu Tơn