Bài 4. Phép đối Xứng Tâm - Củng Cố Kiến Thức

Trang chủ » đối Xứng Tâm O » Bài 4. Phép đối Xứng Tâm - Củng Cố Kiến Thức

Có thể bạn quan tâm

SureLRN THÔNG BÁO Bạn có 0 thông báo mới Đang tải thông báo ...
Xem tất cả
  1. Trang chủ
  2. Củng cố kiến thức
  3. Lớp 11
  4. Toán

Bài 4. Phép đối xứng tâm

I. Định nghĩa

Cho điểm $I$. Phép biến hình biến điểm $I$ thành chính nó, biến mỗi điểm M khác $I$ thành M’ sao cho $I$ là trung điểm của đoạn thẳng MM’ được gọi là phép đối xứng tâm $I$.

II. Biểu thức tọa độ của phép đối xứng qua gốc tọa độ

Trong mặt phẳng tọa độ Oxy, cho $I = \left( {{x_0};{y_0}} \right)$, gọi $M = \left( {x;y} \right)$ và $M' = \left( {x';y'} \right)$ là ảnh của M qua phép đối xứng tâm $I$. Khi đó:

$\left\{ \begin{array}{l} x' = 2{x_0} - x\\ y' = 2{y_0} - y \end{array} \right.$

III. Tính chất

* Tính chất 1

Nếu Đ1(M) = M’ và Đ1(N) = N’ thì $\overrightarrow {M'N'} = \overrightarrow { - MN} $, từ đó suy ra $M'N' = MN$.

* Tính chất 2

Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

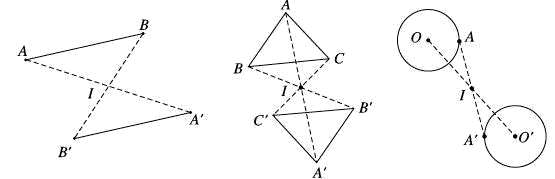
IV. Tâm đối xứng của một hình

Điểm $I$ được gọi là tâm đối xứng của hình Hnếu phép đối xứng tâm $I$ biến Hthành chính nó.

Khi đó Hlà hình có tâm đối xứng.

Bài tập

Bạn chưa đăng nhập !

Vui lòng đăng nhập trước khi thực hiện thao tác này.

Đăng nhập Quay lại Đồng ý Đóng

Từ khóa » đối Xứng Tâm O