Bài 4: Phép đối Xứng Tâm - Hoc24
Có thể bạn quan tâm
I. ĐỊNH NGHĨA
Cho điểm \(I\). Phép biến hình biến điểm \(I\) thành chính nó, biến mỗi điểm \(M\) khác \(I\) thành \(M'\) sao cho \(I\) là trung điểm của đoạn thẳng \(MM'\) được gọi là phép đối xứng tâm \(I\).
Điểm \(I\) được gọi là tâm đối xứng.

Phép đối xứng tâm \(I\) thường được kí hiệu là \(Đ_I\).
Từ định nghĩa trên ta suy ra
\(M'=Đ_I\left(M\right)\Leftrightarrow\overrightarrow{IM'}=-\overrightarrow{IM}\)
Nhận xét: \(M'=Đ_I\left(M\right)\Leftrightarrow M=Đ_I\left(M'\right)\)
Ví dụ: Trong hình vẽ dưới đây, các điểm \(X,Y,Z\) tương ứng là ảnh của các điểm \(D,E,C\) qua phép đối xứng tâm \(I\) và ngược lại:

Nếu hình \(H'\) là ảnh của hình \(H\) qua \(Đ_I\) thì ta còn nói \(H'\) đối xứng với \(H\) qua tâm \(I\), hay \(H\) và \(H'\) đối xứng qua tâm \(I\).
Ví dụ 1: Trong mặt phẳng toạ độ \(Oxy\) cho điểm \(A\left(1;2\right)\) và điểm \(I\left(3;2\right)\). Tìm ảnh của điểm \(A\) qua phép đối xứng tâm \(I\).
Giải:
Gọi \(B\) là ảnh của điểm \(A\) qua phép đối xứng tâm \(I\)
Thì ta có \(I\) là trung điểm của đoạn thẳng \(AB\) \(\Rightarrow\) \(\left\{{}\begin{matrix}\dfrac{x_A+x_B}{2}=x_I\\\dfrac{y_A+y_B}{2}=y_I\end{matrix}\right.\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}x_B=2x_I-x_A=2.3-1=5\\y_B=2y_I-y_A=2.2-2=2\end{matrix}\right.\) \(\Rightarrow\) \(B\left(5;2\right)\)
Vậy \(B\left(5;2\right)\) là ảnh của điểm \(A\) qua phép đối xứng tâm \(I\).
@2095029@II. BIỂU THỨC TOẠ ĐỘ CỦA PHÉP ĐỐI XỨNG QUA GỐC TOẠ ĐỘ
Trong hệ toạ độ \(Oxy\) cho điểm \(M\left(x;y\right)\), \(M'=Đ_I\left(M\right)=\left(x';y'\right)\) , khi đó \(\left\{{}\begin{matrix}x'=-x\\y'=-y\end{matrix}\right.\).
Biểu thức này được gọi là biểu thức toạ độ của phép đối xứng qua gốc toạ độ.
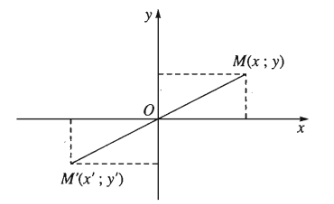
Ví dụ 2: Trong mặt phẳng \(Oxy\) cho điểm \(A\left(-4;3\right)\). Tìm ảnh của \(A\) qua phép đối xứng tâm \(O\)
Giải:
Gọi \(A'\left(a;b\right)\) là ảnh của \(A\) qua phép đối xứng tâm \(O\)
Theo biểu thức toạ độ của phép đối xứng qua gốc toạ độ ta có:
\(\left\{{}\begin{matrix}a=-\left(-4\right)\\b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=-3\end{matrix}\right.\)
Vậy \(A'\left(4;-3\right)\) ảnh của \(A\) qua phép đối xứng tâm \(O\).
@51019@III. TÍNH CHẤT
a) Tính chất 1:
Nếu \(Đ_I\left(M\right)=M'\) và \(Đ_I\left(N\right)=N'\) thì \(\overrightarrow{M'N'}=-\overrightarrow{MN}\), từ đó suy ra \(M'N'=MN\).
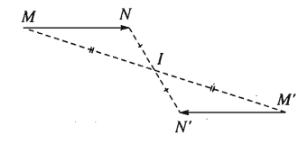
Thật vậy, vì \(\overrightarrow{IM'}=-\overrightarrow{IM}\) và \(\overrightarrow{IN'}=-\overrightarrow{IN}\)
nên \(\overrightarrow{M'N'}=\overrightarrow{IN'}-\overrightarrow{IM'}=-\overrightarrow{IN}-\left(-\overrightarrow{IM}\right)=-\left(\overrightarrow{IN}-\overrightarrow{IM}\right)=-\overrightarrow{MN}\).
Nói cách khác, phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì.b) Tính chất 2:
Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
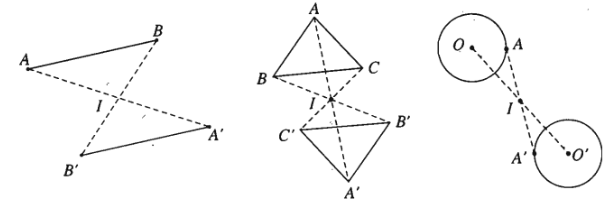
Ví dụ 3: Trong mặt phẳng \(Oxy\) cho đường thẳng \(\left(d\right):x-2y+3=0\) . Tìm ảnh của \(\left(d\right)\) qua phép đối xứng tâm \(O\).
Giải:
Gọi \(\left(d'\right)\) là ảnh của \(\left(d\right)\) qua phép đối xứng tâm \(O\).
Vì \(O\notin\left(d\right)\) nên ta có \(\left(d'\right)\) // \(\left(d\right)\)
Suy ra \(\left(d'\right)\) có dạng \(x-2y+m=0\).
Lấy điểm \(A\left(-3;0\right)\in\left(d\right)\), \(Đ_O\left(A\right)=A'\in\left(d'\right)\)
Ta có \(\left\{{}\begin{matrix}x_{A'}=-x_A=-\left(-3\right)=3\\y_{A'}=-y_A=-0=0\end{matrix}\right.\) \(\Rightarrow A'\left(3;0\right)\in\left(d'\right)\)
Thay vào phương trình \(x-2y+m=0\) ta được \(m=-3\)
Vậy ảnh của \(\left(d\right)\) qua phép đối xứng tâm \(O\) là đường thẳng \(\left(d'\right)\): \(x-2y-3=0\).
Ví dụ 4: Cho đường tròn \(\left(C\right):\left(x-2\right)^2+\left(y+4\right)^2=5\). Tìm phương trình đường tròn \(\left(C'\right)\) là ảnh của \(\left(C\right)\) qua phép đối xứng tâm \(O\) .
Giải:Đường tròn \(\left(C\right)\) có tâm \(I\left(2;-4\right)\) và bán kính \(R=\sqrt{5}\)
Do đó \(\left(C'\right)\) có tâm \(I'=Đ_O\left(I\right)=\left(2;-4\right)\) và bán kính \(R=\sqrt{5}\)
Vậy \(\left(C'\right)\): \(\left(x+2\right)^2+\left(y-4\right)^2=5\).
@50915@IV. TÂM ĐỐI XỨNG CỦA MỘT HÌNH
Định nghĩa:
Điểm \(I\) được gọi là tâm đối xứng của hình \(H\) nếu phép đối xứng tâm \(I\) biến \(H\) thành chính nó.
Khi đó ta nói \(H\) là hình có tâm đối xứng.
Ví dụ: Các hình sau là các hình có tâm đối xứng:
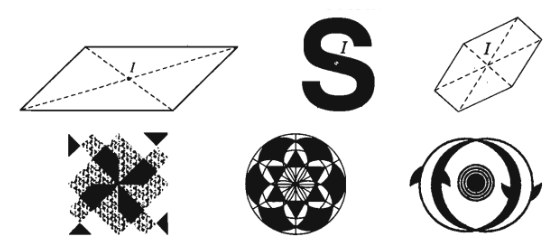
Từ khóa » Ví Dụ Phép đối Xứng Tâm
-
Hình Học 11 Bài 4: Phép đối Xứng Tâm - HOC247
-
Bài 4: Phép đối Xứng Tâm - Tìm đáp án, Giải Bài Tập, để Học Tốt
-
Phép Đối Xứng Tâm: Lý Thuyết, Công Thức Và Bài Tập (Có Đáp Án)
-
Phép Đối Xứng Tâm
-
Các Bài Toán Về Phép đối Xứng Tâm Và Cách Giải
-
Công Thức Về Phép đối Xứng Tâm Hay Nhất | Toán Lớp 11
-
Phép đối Xứng Tâm - Nội Dung Lý Thuyết Và Các Dạng Bài Tập
-
Phép đối Xứng Tâm-Học Toán 11 - Itoan
-
Phép đối Xứng Tâm, Trắc Nghiệm Toán Học Lớp 11 - Baitap123
-
Phép đối Xứng Tâm Là Gì? Các Dạng Toán Của Phép đối Xứng Tâm
-
Phép đối Xứng Tâm – Bài Tập Hình Học Lớp 11
-
Lý Thuyết, Các Dạng Toán Và Bài Tập Phép đối Xứng Tâm
-
Các Dạng Toán Phép đối Xứng Tâm
-
Soạn Hình Học 11 Bài 4: Phép đối Xứng Tâm