Bài 4: Thuật Toán Tìm Kiếm Theo Chiều Sâu DFS Pascal C++
Có thể bạn quan tâm
Thuật toán tìm kiếm theo chiều sâu DFS là thuật toán tìm kiếm trên cây hoặc đồ thị. Thuật toán này khác với BFS ở chỗ BFS duyệt theo chiều rộng (những đỉnh gần đỉnh gốc sẽ được thăm trước), còn DFS duyệt theo chiều sâu (Xuất phát từ đỉnh gốc, từ đỉnh đó phát triển xa nhất có thể theo mỗi nhánh)
1. Ý tưởng và cài đặt thuật toán DFS
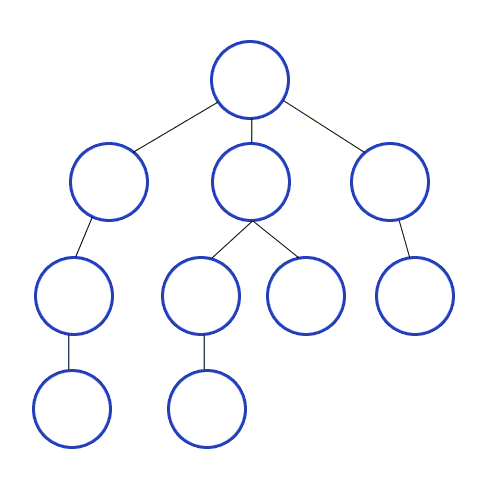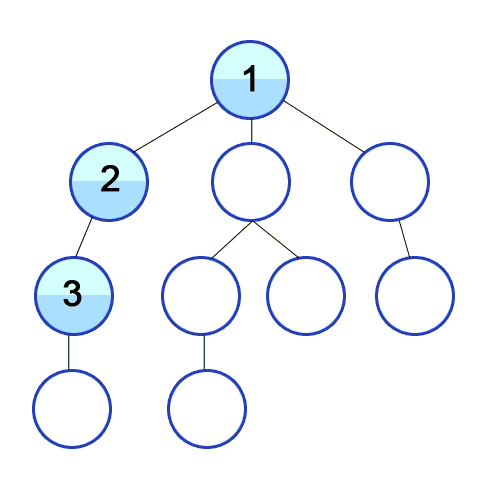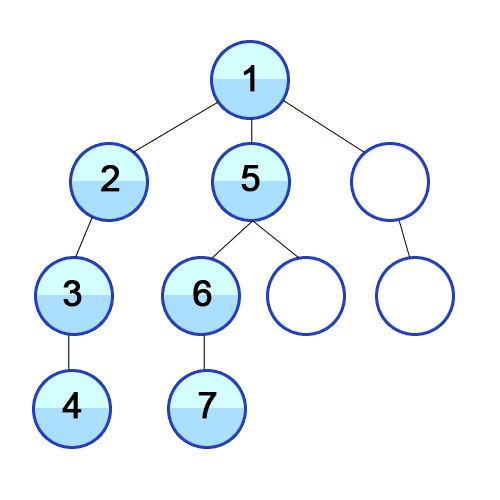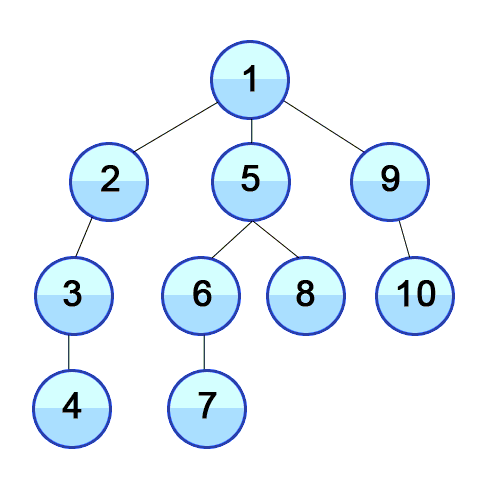
Hình ảnh minh họa DFS, nguồn wikipedia
Tư tưởng thuật toán có thể trình bày như sau: Từ một đỉnh S ban đầu ta sẽ có các đỉnh kề là x, từ đỉnh x ta sẽ có các đỉnh kề là y, và nó cũng thuộc nhánh s-x-y… Chúng ta thăm các nhánh đó theo chiều sâu (thăm đến khi không còn đỉnh kề chưa duyệt). Điều đó gợi cho chúng ta viết một thủ tục đệ quy DFS(u) để mô tả việc duyệt từ đỉnh u sang đỉnh kề v chưa được thăm.
Bạn có thể tham khảo thêm:
Thuật toán tìm kiếm theo chiều rộng BFS pascal c++
a. Mô hình giải thuật DFS
Giải thuật DFS có thể viết theo mô hình dưới đây:
void dfs(int u) { free[u]=false; // đánh dấu đỉnh u đã được thăm for (int v=1; v<=n; v++) if ((tồn tại cạnh u, v) và (free[u][v]==true)) // tồn tại đỉnh kề với u, chưa được thăm dfs(v); //duyệt đỉnh v }b. Đề bài ví dụ
Ví dụ: Viết chương trình ghi ra thứ tự duyệt DFS xuất phát từ đỉnh s. Đồ thi gồm n đỉnh, m cạnh 2 chiều, các thành phần trên đồ thị liên thông với nhau.
Dữ liệu vào:
- Dòng đầu: gồm 3 số nguyên n, m, s (1<=n, m<=100, 1<=s<=n)
- M dòng tiếp theo: mỗi dòng gồm 2 số u, v, mô tả 1 cạnh trong đồ thị
Dữ liệu ra:
- Gồm nhiều dòng, là thứ tự duyệt DFS
c. Code thuật toán DFS
1. Code DFS C++ tổ chức ma trận kề
Tham khảo thêm về ma trận kề: https://kienthuc24h.com/ma-tran-ke-cpascal-ly-thuyet-thi/
#include <bits/stdc++.h> using namespace std; int a[101][101]; int n, m, Free[101], u, v, s; void DFS(int u) { cout << u << endl; Free[u] = false; for (int v = 1; v <= n; v++) if (a[u][v] == 1 && Free[v]) DFS(v); } int main() { cin >> n >> m >> s; for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) a[i][j] = 0; for (int i = 1; i <= m; i++) { cin >> u >> v; a[u][v] = 1; a[v][u] = 1; } for (int i = 1; i <= n; i++) Free[i] = 1; DFS(s); return 0; }2. Code DFS Pascal tổ chức ma trận kề
Const maxn = 101; Var a : array [1..maxn,1..maxn] of boolean; free : array [1..maxn] of boolean; Q : array [1..maxn] of integer; n, m, s: integer; dau, cuoi : integer; Procedure init; Begin fillchar(a,sizeof(a),false); fillchar(Free,sizeof(Free),true); end; Procedure readf; Var i, u, v : integer; Begin readln(n,m,s); for i := 1 to m do begin readln(u,v); A[u,v] := true; A[v,u] := true; end; end; Procedure DFS(u : integer); Var v : integer; Begin writeln(u); Free[u] := false; For v := 1 to n do If A[u,v] and Free[v] then dfs(v); end; Procedure main; Var i : integer; Begin init; readf; DFS(s); end; BEGIN main; END.d. Test ví dụ
Các bạn có thể thử các bộ test sau:
Test 1:
| Input | Output |
| 7 7 11 2 1 3 1 5 2 4 2 6 3 7 5 6 | 1 2 4 6 5 3 7 |
Test 2:
| Input | Output |
| 7 7 41 2 1 3 1 5 2 4 2 6 3 7 5 6 | 4 2 1 3 7 5 6 |
2. Độ phức tạp DFS
Độ phức tạp thời gian: O(|V|+|E|) với |V| là số đỉnh của đồ thị, |E| là số cạnh
3. Bài tập ứng dụng thuật toán DFS
Bạn có thể áp dụng ngay để làm các bài tập sau về DFS:
Yêu cầu hiểu về thành phần liên thông VBGRASS spoj – Bãi cỏ ngon nhất BCLKCOUN spoj PTIT – Đếm số ao
MTNTRAI spoj THPTCBT – 21697. Nông Trại
BCISLAND PTIT spoj – Nước biển
ADS spoj – Quảng cáo
Yêu cầu có kiến thức về cầu – khớp
BCACM11E spoj PTIT – Phương án bắn pháo
Từ khóa » Bài Tập Dfs
-
Cây DFS (Depth-First Search Tree) Và ứng Dụng - VNOI
-
Các Chủ đề Cơ Bản Về đồ Thị - VNOI
-
Bài Tập Về đồ Thị (DFS, BFS, Vùng Liên Thông)
-
DFSDEMO - Minh Họa Thuật Toán DFS (cơ Bản) - Bài Tập
-
Tài Liệu Bồi Dưỡng Học Sinh Giỏi Môn Tin Học Thpt Chuyên đề ứng ...
-
[PDF] Toán Rời Rạc 2,ngô Xuân Bách,hvcnbcvt
-
Chuyen Dề ứng Dụng Duyệt đồ Thị - Trường THPT Chuyên Lào Cai
-
Các Giải Thuật Tìm Kiếm Trên đồ Thị - Viblo
-
Chuyên đề Một Số Bài Tập ứng Dụng Của Tìm Kiếm ưu Tiên Theo Chiều ...
-
Thuật Toán Về Tìm Kiếm Theo Chiều Sâu DFS Bằng Ngôn Ngữ C/C++
-
DFS – BFS | LÀM HẾT MÌNH
-
[Bài Tập] Các Bài Tập Pascal Về DFS - BFS - Tin Học Việt
-
Tìm Kiếm Theo Chiều Sâu DFS - Depth First Search - Toán Rời Rạc