Bài 40. Cách Tính Số Fibonacci Trong C/C++

Chắc các bạn cũng đã biết dãy Fibonacci là gì rồi. Đó là dãy số mà số tiếp theo là tổng của hai số liền trước, ví dụ: 1, 1, 2, 3, 5, 8, 13, …. Bài viết này sẽ hướng dẫn cho các bạn cách tính số fibonacci bằng phương pháp dùng đệ quy và không dùng đệ quy.

1. Dùng đệ quy để tính số fibonacci
2. Cách tính số Fibonacci không dùng đệ quy
3. Tìm 1000 số Fibonacci đầu tiên

Dùng đệ quy để tính số fibonacci

Công thức truy hồi của dãy fibonacci có dạng: f(n) = f(n-1) + f(n-2) .

Với f(1) = 1;  f(2) =1;

Cách tính số Fibonacci trong C

#include <stdio.h> #include <conio.h> int Fibonacci(int n) { if (n == 1 || n == 2) return 1; return Fibonacci(n - 1) + Fibonacci(n - 2); } int main() { int n; printf("nhap n: "); scanf("%d", &n); printf("So Fibonacci thu %d la: %d", n, Fibonacci(n)); return 0; }nhap n: 6 So Fibonacci thu 6 la: 8

Cách tính số Fibonacci trong C++

#include <iostream> using namespace std; int Fibonacci(int n) { if (n == 1 || n == 2) return 1; return Fibonacci(n - 1) + Fibonacci(n - 2); } int main() { int n; cout << "nhap n: "; cin >> n; cout << "So Fibonacci thu " << n << " la: " << Fibonacci(n); return 0; } nhap n: 6 So Fibonacci thu 6 la: 8

Khi đã có hệ thức truy hồi thì việc viết hàm đệ quy rất đơn giản phải không nào ? Nhưng liệu bạn có thử nhập n lớn ( cỡ 30 – 40 ) không ạ. Nếu thử rồi thì chắc các bạn cũng thấy nó chậm hơn rất nhiều. Nguyên nhân là khi tính số fibonacci thứ 5 chương trình sẽ yêu cầu tính hai số fibonacci thứ 4 và thứ 3. Nó lại tiếp tục như vậy đến khi tính được số fibonacci thứ 2 hoặc thứ 1 mới dừng lại.

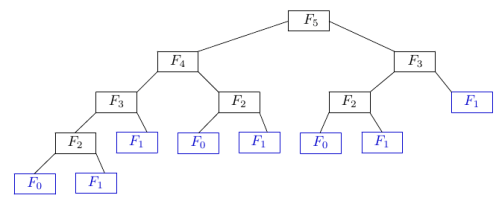
Vậy nếu muốn chương trình của chúng ta chạy nhanh hơn thì chúng ta phải khử đệ quy. Cùng làm nhé !

Cách tính số Fibonacci không dùng đệ quy

Ý tưởng cách này là chúng ta sẽ dùng một vòng lặp để tính số Fibonacci .

• Nếu n = 1 hoặc n = 2 thì chúng ta return 1
• Sau đó tạo một biến i có giá trị bằng 3
• Trong vòng while chúng ta tính a = a1 + a2
• Sau đó gán a1 = a2 và a2 = a cứ chạy đến khi nào i = n thì dừng

#include <stdio.h> int Fibonacci(int n) { int a1 = 1, a2 = 1; if (n == 1 || n == 2) return 1; int i = 3, a; while (i <= n) { a = a1 + a2; a1 = a2; a2 = a; i++; } return a; } int main() { int n; printf("nhap n: "); scanf("%d", &n); printf("So Fibonacci thu %d la: %d", n, Fibonacci(n)); return 1; }nhap n: 40 So Fibonacci thu 40 la: 102334155

Cách tính số Fibonacci trong C++

#include <iostream> using namespace std; int Fibonacci(int n) { int a1 = 1, a2 = 1; if (n == 1 || n == 2) return 1; int i = 3, a; while (i <= n) { a = a1 + a2; a1 = a2; a2 = a; i++; } return a; } int main() { int n; cout << "nhap n: "; cin >> n; cout << "So Fibonacci thu " << n << " la: " << Fibonacci(n); return 1; }nhap n: 40 So Fibonacci thu 40 la: 102334155

Tìm 1000 số Fibonacci đầu tiên

Với code trên bạn tìm đến số Fibo thứ 50 là bị tràn số rồi. Code với số nguyên lớn dưới đây sẽ giúp bạn tính được số Fibo thứ 1000 hoặc hơn thế nữa. Có thể bạn sẽ cần đọc bài viết dưới đây trước khi tham khảo code này.

Cộng trừ nhân chia 2 số nguyên lớn trong C/C++

[wpcc-iframe class=”wp-embedded-content” sandbox=”allow-scripts” security=”restricted” style=”position: absolute; clip: rect(1px, 1px, 1px, 1px);” title=”“Cộng trừ nhân chia 2 số nguyên lớn trong C/C++” — Luyện Code” src=”https://nguyenvanhieu.vn/cong-tru-nhan-chia-2-so-nguyen-lon/embed/#?secret=NnOp7CYZm7%23?secret=1H7BE6XQIF” data-secret=”1H7BE6XQIF” width=”600″ height=”338″ frameborder=”0″ marginwidth=”0″ marginheight=”0″ scrolling=”no”]

Lời giải cho chương trình in ra 1000 số Fibo đầu tiên.

#include <bits/stdc++.h> using namespace std; const int base = 1000000000; const int base_digits = 9; struct bigint { vector<int> a; int sign; bigint() : sign(1) { } bigint(long long v) { *this = v; } bigint(const string &s) { read(s); } void operator=(const bigint &v) { sign = v.sign; a = v.a; } void operator=(long long v) { sign = 1; if (v < 0) sign = -1, v = -v; for (; v > 0; v = v / base) a.push_back(v % base); } bigint operator+(const bigint &v) const { if (sign == v.sign) { bigint res = v; for (int i = 0, carry = 0; i < (int)max(a.size(), v.a.size()) || carry; ++i) { if (i == (int)res.a.size()) res.a.push_back(0); res.a[i] += carry + (i < (int)a.size() ? a[i] : 0); carry = res.a[i] >= base; if (carry) res.a[i] -= base; } return res; } return *this - (-v); } bigint operator-(const bigint &v) const { if (sign == v.sign) { if (abs() >= v.abs()) { bigint res = *this; for (int i = 0, carry = 0; i < (int)v.a.size() || carry; ++i) { res.a[i] -= carry + (i < (int)v.a.size() ? v.a[i] : 0); carry = res.a[i] < 0; if (carry) res.a[i] += base; } res.trim(); return res; } return -(v - *this); } return *this + (-v); } void operator*=(int v) { if (v < 0) sign = -sign, v = -v; for (int i = 0, carry = 0; i < (int)a.size() || carry; ++i) { if (i == (int)a.size()) a.push_back(0); long long cur = a[i] * (long long)v + carry; carry = (int)(cur / base); a[i] = (int)(cur % base); //asm("divl %%ecx" : "=a"(carry), "=d"(a[i]) : "A"(cur), "c"(base)); } trim(); } bigint operator*(int v) const { bigint res = *this; res *= v; return res; } friend pair<bigint, bigint> divmod(const bigint &a1, const bigint &b1) { int norm = base / (b1.a.back() + 1); bigint a = a1.abs() * norm; bigint b = b1.abs() * norm; bigint q, r; q.a.resize(a.a.size()); for (int i = a.a.size() - 1; i >= 0; i--) { r *= base; r += a.a[i]; int s1 = r.a.size() <= b.a.size() ? 0 : r.a[b.a.size()]; int s2 = r.a.size() <= b.a.size() - 1 ? 0 : r.a[b.a.size() - 1]; int d = ((long long)base * s1 + s2) / b.a.back(); r -= b * d; while (r < 0) r += b, --d; q.a[i] = d; } q.sign = a1.sign * b1.sign; r.sign = a1.sign; q.trim(); r.trim(); return make_pair(q, r / norm); } bigint operator/(const bigint &v) const { return divmod(*this, v).first; } bigint operator%(const bigint &v) const { return divmod(*this, v).second; } void operator/=(int v) { if (v < 0) sign = -sign, v = -v; for (int i = (int)a.size() - 1, rem = 0; i >= 0; --i) { long long cur = a[i] + rem * (long long)base; a[i] = (int)(cur / v); rem = (int)(cur % v); } trim(); } bigint operator/(int v) const { bigint res = *this; res /= v; return res; } int operator%(int v) const { if (v < 0) v = -v; int m = 0; for (int i = a.size() - 1; i >= 0; --i) m = (a[i] + m * (long long)base) % v; return m * sign; } void operator+=(const bigint &v) { *this = *this + v; } void operator-=(const bigint &v) { *this = *this - v; } void operator*=(const bigint &v) { *this = *this * v; } void operator/=(const bigint &v) { *this = *this / v; } bool operator<(const bigint &v) const { if (sign != v.sign) return sign < v.sign; if (a.size() != v.a.size()) return a.size() * sign < v.a.size() * v.sign; for (int i = a.size() - 1; i >= 0; i--) if (a[i] != v.a[i]) return a[i] * sign < v.a[i] * sign; return false; } bool operator>(const bigint &v) const { return v < *this; } bool operator<=(const bigint &v) const { return !(v < *this); } bool operator>=(const bigint &v) const { return !(*this < v); } bool operator==(const bigint &v) const { return !(*this < v) && !(v < *this); } bool operator!=(const bigint &v) const { return *this < v || v < *this; } void trim() { while (!a.empty() && !a.back()) a.pop_back(); if (a.empty()) sign = 1; } bool isZero() const { return a.empty() || (a.size() == 1 && !a[0]); } bigint operator-() const { bigint res = *this; res.sign = -sign; return res; } bigint abs() const { bigint res = *this; res.sign *= res.sign; return res; } long long longValue() const { long long res = 0; for (int i = a.size() - 1; i >= 0; i--) res = res * base + a[i]; return res * sign; } friend bigint gcd(const bigint &a, const bigint &b) { return b.isZero() ? a : gcd(b, a % b); } friend bigint lcm(const bigint &a, const bigint &b) { return a / gcd(a, b) * b; } void read(const string &s) { sign = 1; a.clear(); int pos = 0; while (pos < (int)s.size() && (s[pos] == '-' || s[pos] == '+')) { if (s[pos] == '-') sign = -sign; ++pos; } for (int i = s.size() - 1; i >= pos; i -= base_digits) { int x = 0; for (int j = max(pos, i - base_digits + 1); j <= i; j++) x = x * 10 + s[j] - '0'; a.push_back(x); } trim(); } friend istream &operator>>(istream &stream, bigint &v) { string s; stream >> s; v.read(s); return stream; } friend ostream &operator<<(ostream &stream, const bigint &v) { if (v.sign == -1) stream << '-'; stream << (v.a.empty() ? 0 : v.a.back()); for (int i = (int)v.a.size() - 2; i >= 0; --i) stream << setw(base_digits) << setfill('0') << v.a[i]; return stream; } static vector<int> convert_base(const vector<int> &a, int old_digits, int new_digits) { vector<long long> p(max(old_digits, new_digits) + 1); p[0] = 1; for (int i = 1; i < (int)p.size(); i++) p[i] = p[i - 1] * 10; vector<int> res; long long cur = 0; int cur_digits = 0; for (int i = 0; i < (int)a.size(); i++) { cur += a[i] * p[cur_digits]; cur_digits += old_digits; while (cur_digits >= new_digits) { res.push_back(int(cur % p[new_digits])); cur /= p[new_digits]; cur_digits -= new_digits; } } res.push_back((int)cur); while (!res.empty() && !res.back()) res.pop_back(); return res; } typedef vector<long long> vll; static vll karatsubaMultiply(const vll &a, const vll &b) { int n = a.size(); vll res(n + n); if (n <= 32) { for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) res[i + j] += a[i] * b[j]; return res; } int k = n >> 1; vll a1(a.begin(), a.begin() + k); vll a2(a.begin() + k, a.end()); vll b1(b.begin(), b.begin() + k); vll b2(b.begin() + k, b.end()); vll a1b1 = karatsubaMultiply(a1, b1); vll a2b2 = karatsubaMultiply(a2, b2); for (int i = 0; i < k; i++) a2[i] += a1[i]; for (int i = 0; i < k; i++) b2[i] += b1[i]; vll r = karatsubaMultiply(a2, b2); for (int i = 0; i < (int)a1b1.size(); i++) r[i] -= a1b1[i]; for (int i = 0; i < (int)a2b2.size(); i++) r[i] -= a2b2[i]; for (int i = 0; i < (int)r.size(); i++) res[i + k] += r[i]; for (int i = 0; i < (int)a1b1.size(); i++) res[i] += a1b1[i]; for (int i = 0; i < (int)a2b2.size(); i++) res[i + n] += a2b2[i]; return res; } bigint operator*(const bigint &v) const { vector<int> a6 = convert_base(this->a, base_digits, 6); vector<int> b6 = convert_base(v.a, base_digits, 6); vll a(a6.begin(), a6.end()); vll b(b6.begin(), b6.end()); while (a.size() < b.size()) a.push_back(0); while (b.size() < a.size()) b.push_back(0); while (a.size() & (a.size() - 1)) a.push_back(0), b.push_back(0); vll c = karatsubaMultiply(a, b); bigint res; res.sign = sign * v.sign; for (int i = 0, carry = 0; i < (int)c.size(); i++) { long long cur = c[i] + carry; res.a.push_back((int)(cur % 1000000)); carry = (int)(cur / 1000000); } res.a = convert_base(res.a, 6, base_digits); res.trim(); return res; } }; int main() { bigint first, second, temp; first = 1; second = 1; int i = 3; cout << 1 << " " << first << "n"; cout << 2 << " " << second << "n"; while (i < 1000) { i++; temp = first + second; cout << i << " " << temp << "n"; first = second; second = temp; } }

Dưới đây là giá trị của số Fibo thứ 1000:

26863810024485359386146727202142923967616609318986952340123175997617981700247881689338369654483356564191827856161443356312976673642210350324634850410377680367334151172899169723197082763985615764450078474174626

Theo dõi lập trình không khó tại:

• Forum: https://www.facebook.com/groups/LapTrinhKhongKho/
• Youtube: https://www.youtube.com/HieuNguyenVanOfficial