Bài 54 Trang 97 SBT Toán 8 Tập 2 - Tìm đáp án

Trang chủ » Khái Niệm 2 Tam Giác đồng Dạng Sbt » Bài 54 Trang 97 SBT Toán 8 Tập 2 - Tìm đáp án

Có thể bạn quan tâm

Đề bài

Tứ giác \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O,\) \(\widehat {ABD} = \widehat {ACD}\). Gọi \(E\) là giao điểm của hai đường thẳng \(AD\) và \(BC\) (h.39)

Chứng minh rằng :

a) \(∆ AOB\) đồng dạng \(∆ DOC\)

b) \(∆ AOD\) đồng dạng \(∆ BOC\)

c) \(EA.ED = EB.EC\).

Phương pháp giải - Xem chi tiết

Sử dụng:

- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

- Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đồng dạng.

Lời giải chi tiết

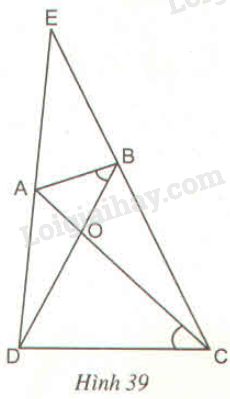
a) \(\widehat {ABD} = \widehat {ACD}\) (gt) hay \(\widehat {ABO} = \widehat {OCD}\)

Xét \(∆ AOB\) và \(∆ DOC\) có:

+) \(\widehat {ABO} = \widehat {OCD}\) (chứng minh trên)

+) \(\widehat {AOB} = \widehat {DOC}\) (đối đỉnh)

\(\Rightarrow  ∆ AOB\) đồng dạng \(∆ DOC\) (g.g)

b) Vì \(∆ AOB\) đồng dạng \(∆ DOC \) suy ra  \(\displaystyle {{AO} \over {OB}} = {{DO} \over {OC}}\)

Xét \(∆ AOD\) và \(∆ BOC\) có:

\(\displaystyle {{AO} \over {OB}} = {{DO} \over {OC}}\) (chứng minh trên)

\(\widehat {AOD} = \widehat {BOC}\) (đối đỉnh)

\(\Rightarrow ∆ AOD\) đồng dạng \(∆ BOC\) (c.g.c)

c) Vì \(∆ AOD\) đồng dạng \(∆ BOC\) suy ra \(\widehat {ADO} = \widehat {BCO}\) hay \(\widehat {EDB} = \widehat {ECA}\)

Xét \(∆ EDB\) và \(∆ ECA\) có:

+) \(\widehat E\) chung

+) \(\widehat {EDB} = \widehat {ECA}\) (chứng minh trên)

\(\Rightarrow ∆ EDB\) đồng dạng \(∆ ECA \) (g.g)

\(\Rightarrow \displaystyle{{ED} \over {EC}} = {{EB} \over {EA}}\)

\(\Rightarrow ED.EA = EC.EB\)

Từ khóa » Khái Niệm 2 Tam Giác đồng Dạng Sbt