Bài 6 (SGK Trang 50)Xác định Tọa độ Của đỉnh, Phương Trình Của Trục ...

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Tất cả
• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Hãy tham gia nhóm Học sinh Hoc24OLM Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Câu hỏi

Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay

• Pham Trong Bach

10 tháng 5 2019 lúc 16:50

Xác định tọa độ đỉnh, phương trình của trục đối xứng của parabol y = ax2 + bx + c.

Xem chi tiết Lớp 10 Toán 1 0 Gửi Hủy Cao Minh Tâm 10 tháng 5 2019 lúc 16:51

Parabol y = ax2 + bx + c có:

+ Tọa độ đỉnh D là:

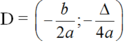
+ Phương trình trục đối xứng là:

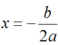
Đúng 0 Bình luận (0) Gửi Hủy

• Bài 6

SGK trang 50 29 tháng 3 2017 lúc 10:46

Xác định tọa độ của đỉnh, phương trình của trục đối xứng của parabol :

                      \(y=ax^2+bx+c\)

Xem chi tiết Lớp 10 Toán Ôn tập chương II 1 0 Gửi Hủy qwerty 30 tháng 3 2017 lúc 7:59

Tọa độ đỉnh \(\left(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\right)\)

Trục đối xứng \(x=\dfrac{-b}{2a}\)

Đúng 0 Bình luận (0) Gửi Hủy

• pham kiet

19 tháng 12 2023 lúc 22:10

Xác định phương trình của Parabol (P): y = x2 + bx + c (P) có tọa độ đỉnh là S(-4;7).vậy (P) cắt trục hoành bao nhiêu độ

 

Xem chi tiết Lớp 10 Toán 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 20 tháng 12 2023 lúc 7:36

        

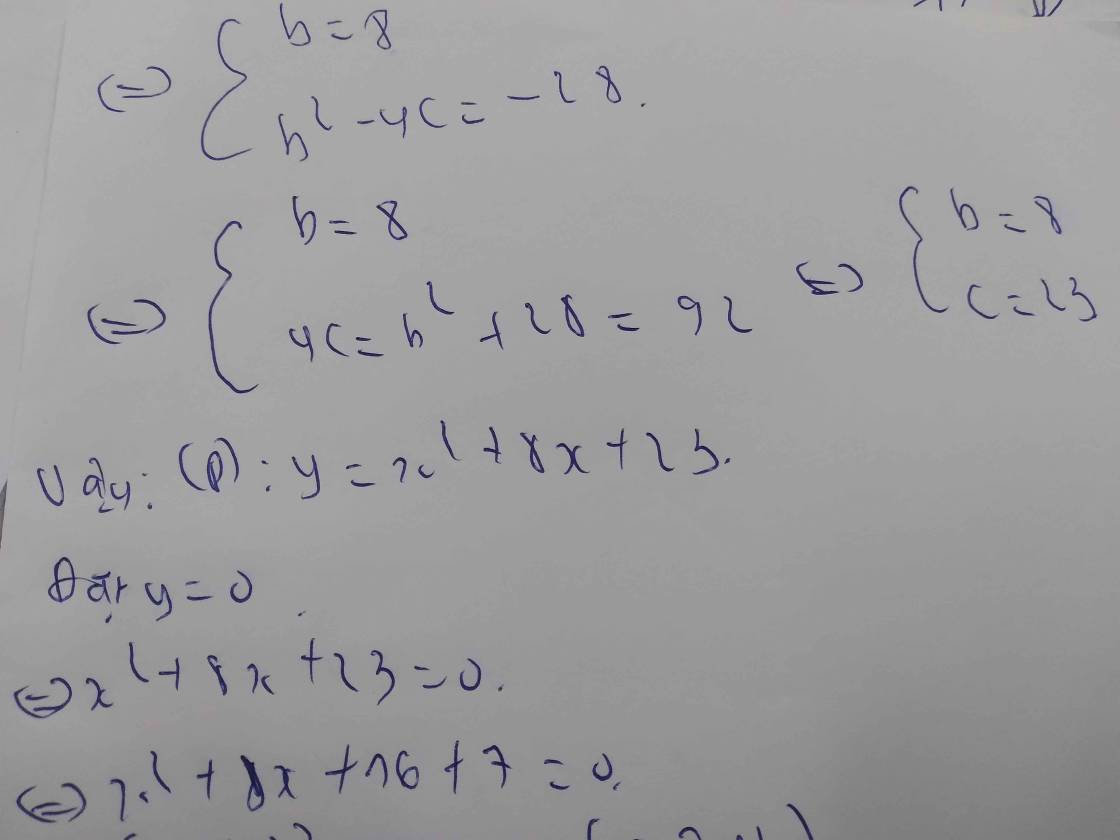
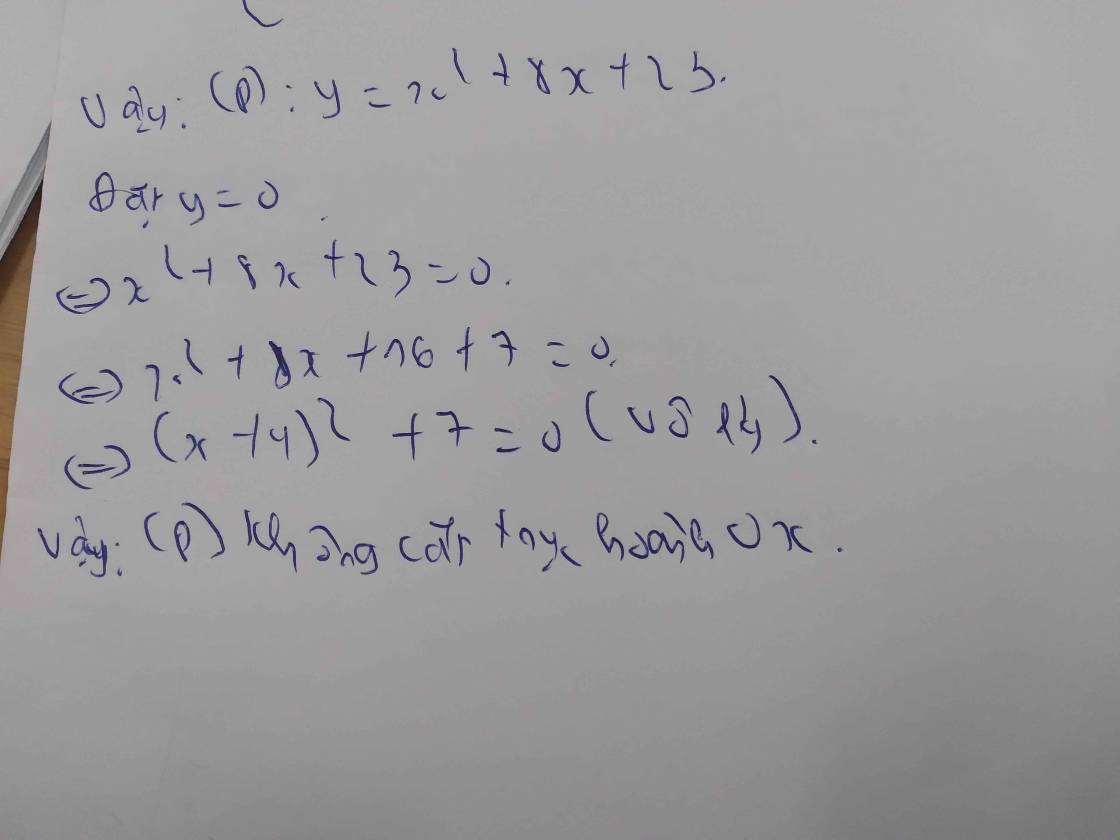
Đúng 0 Bình luận (0) Gửi Hủy

• Pham Trong Bach

20 tháng 12 2019 lúc 10:08

Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.

  y   =   2 x 2 -   x   -   2

Xem chi tiết Lớp 10 Toán 1 0 Gửi Hủy Cao Minh Tâm 20 tháng 12 2019 lúc 10:09

Ở đây a = 2; b = -2; c = -2. Ta có Δ   =   ( - 1 ) 2   -   4 . 2 . ( - 2 )   =   17

    Trục đối xứng là đường thẳng x = 1/4; đỉnh I(1/4; -17/8) giao với trục tung tại điểm (0; -2).

    Để tìm giao điểm với trục hoành ta giải phương trình

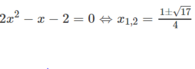
Vậy các giao điểm với trục hoành là

Đúng 0 Bình luận (0) Gửi Hủy

• Pham Trong Bach

26 tháng 6 2019 lúc 16:42

Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.

y   =   - 2 x 2   -   x   +   2

Xem chi tiết Lớp 10 Toán 1 0 Gửi Hủy Cao Minh Tâm 26 tháng 6 2019 lúc 16:43

Trục đối xứng x = -1/4; đỉnh I(-1/4; -17/8) giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm

Đúng 0 Bình luận (0) Gửi Hủy

• Chu Thị Dương

22 tháng 11 2023 lúc 20:49

Câu T. Cho parabol (P): y= x +5x-6. Xác định trục đối xứng, tọa độ đinh của parabol (P), tọa độ giao điểm của parabol (P) với trục hoành.

Xem chi tiết Lớp 10 Toán §2. Hàm số y=ax+b 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 22 tháng 11 2023 lúc 22:45

Sửa đề: (P): \(y=x^2+5x-6\)

Tọa độ đỉnh của (P) là:

\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=-\dfrac{5}{2}\\y=-\dfrac{\text{Δ}}{4a}=-\dfrac{5^2-4\cdot1\cdot\left(-6\right)}{4\cdot1}=-\dfrac{25+24}{4}=-\dfrac{49}{4}\end{matrix}\right.\)

=>Trục đối xứng của (P) là \(x=-\dfrac{5}{2}\)

Tọa độ giao điểm của (P) với trục Ox sẽ là nghiệm của hệ phương trình sau đây:

\(\left\{{}\begin{matrix}x^2+5x-6=0\\y=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\left(x+6\right)\left(x-1\right)=0\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{-6;1\right\}\\y=0\end{matrix}\right.\)

Vậy: Tọa độ các giao điểm của (P) với trục Ox là A(-6;0) và B(1;0)

Đúng 1 Bình luận (0) Gửi Hủy

• Nguyễn Thị Lan Anh

27 tháng 1 2023 lúc 21:47

Xác định trục đối xứng, tọa độ đỉnh , các giao điểm với trục tung và trục hoành của các parabol :

a, y= 2x2-x-2

b,y= -3x2-6x+4

c, y=-2x2-x+2

Xem chi tiết Lớp 10 Toán Ôn tập chương III 1 0 Gửi Hủy Nguyễn Lê Phước Thịnh CTV 28 tháng 1 2023 lúc 0:10

a: Trục đối xứng là x=-(-1)/4=1/4

Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{1}{4}\\y=-\dfrac{\left(-1\right)^2-4\cdot2\cdot\left(-2\right)}{4\cdot2}=-\dfrac{17}{8}\end{matrix}\right.\)

Thay y=0 vào (P), ta được:

2x^2-x-2=0

=>\(x=\dfrac{1\pm\sqrt{17}}{4}\)

thay x=0 vào (P), ta được:

y=2*0^2-0-2=-2

b: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{-\left(-6\right)}{2\cdot\left(-3\right)}=\dfrac{6}{-6}=-1\\y=-\dfrac{\left(-6\right)^2-4\cdot\left(-3\right)\cdot4}{4\cdot\left(-3\right)}=7\end{matrix}\right.\)

=>Trục đối xứng là x=-1

Thay y=0 vào (P), ta được:

-3x^2-6x+4=0

=>3x^2+6x-4=0

=>\(x=\dfrac{-3\pm\sqrt{21}}{3}\)

Thay x=0 vào (P), ta được:

y=-3*0^2-6*0+4=4

c: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{-\left(-1\right)}{2\cdot\left(-2\right)}=\dfrac{1}{-4}=\dfrac{-1}{4}\\y=-\dfrac{\left(-1\right)^2-4\cdot\left(-2\right)\cdot2}{4\cdot\left(-2\right)}=\dfrac{17}{8}\end{matrix}\right.\)

=>Trục đối xứng là x=-1/4

Thay y=0 vào (P), ta được:

-2x^2-x+2=0

=>2x^2+x-2=0

=>\(x=\dfrac{-1\pm\sqrt{17}}{4}\)

Thay x=0 vào (P), ta được:

y=-2*0^2-0+2=2

Đúng 0 Bình luận (0) Gửi Hủy

• ManDoo Ami 태국

12 tháng 8 2021 lúc 21:58

Xác định phương trình của Parabol (P) y = ax\(^2\)+ bx + c biết rằng (P) có đỉnh I ( 1 ; 4 )

Xem chi tiết Lớp 10 Toán Ôn tập chương III 1 0 Gửi Hủy Nguyễn Việt Lâm CTV 12 tháng 8 2021 lúc 22:12

Đề bài thiếu, không thể xác định chính xác (P) khi chỉ biết đỉnh

Đúng 0 Bình luận (0) Gửi Hủy

• Nguyễn Phương Linh

12 tháng 10 2021 lúc 7:36 1. Xác định tọa độ đỉnh, trục đối xứng và giao điểm của parabol với trục tung và trục hoành (nếu có).             a) 𝑦   𝑥2 − 6𝑥 + 5                                                              b) 𝑦   −2𝑥2 + 2𝑥 − 1                          c) 𝑦   −3𝑥2 + 4𝑥 − 1                                                          d) 𝑦 2𝑥2 − 5𝑥 + 2Đọc tiếp

1. Xác định tọa độ đỉnh, trục đối xứng và giao điểm của parabol với trục tung và trục hoành (nếu có).

             a) 𝑦 =  𝑥2 − 6𝑥 + 5                                                              b) 𝑦 =  −2𝑥2 + 2𝑥 − 1           

 

              c) 𝑦 =  −3𝑥2 + 4𝑥 − 1                                                          d) 𝑦 = 2𝑥2 − 5𝑥 + 2

Xem chi tiết Lớp 10 Toán §3. Hàm số bậc hai 0 0 Gửi Hủy

• Bài 7

SGK trang 50 29 tháng 3 2017 lúc 10:47

Xác định tọa độ giao điểm của parabol \(y=ax^2+bx+c\) với trục tung ?

Tìm điều kiện để parabol này cắt trục hoành tại hai điểm phân biệt và viết tọa độ của các giao điểm trong trường hợp đó ?

Xem chi tiết Lớp 10 Toán Ôn tập chương II 1 0 Gửi Hủy Bùi Thị Vân 5 tháng 6 2017 lúc 15:41

Điều kiện để (P): \(y=ax^2+bx+c\) cắt trục hoành tại hai điểm phân biệt là \(\Delta>0\). Gọi \(x_1;x_2\) là hoành độ của hai giao điểm. Ta có: \(x_{1,2}=\dfrac{-b\pm\sqrt{\Delta}}{2a}\); Tọa độ giao điểm là: \(A\left(\dfrac{-b+\sqrt{\Delta}}{2a};0\right)\); \(A\left(\dfrac{-b-\sqrt{\Delta}}{2a};0\right)\).

Đúng 0 Bình luận (0) Gửi Hủy