Bài 6: Thể Tích Của Hình Lăng Trụ đứng - Hoc24

HOC24

Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng

• Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn

Đóng Đăng nhập Đăng ký

Lớp học

• Lớp 12
• Lớp 11
• Lớp 10
• Lớp 9
• Lớp 8
• Lớp 7
• Lớp 6
• Lớp 5
• Lớp 4
• Lớp 3
• Lớp 2
• Lớp 1

Môn học

• Toán
• Vật lý
• Hóa học
• Sinh học
• Ngữ văn
• Tiếng anh
• Lịch sử
• Địa lý
• Tin học
• Công nghệ
• Giáo dục công dân
• Tiếng anh thí điểm
• Đạo đức
• Tự nhiên và xã hội
• Khoa học
• Lịch sử và Địa lý
• Tiếng việt
• Khoa học tự nhiên
• Hoạt động trải nghiệm
• Hoạt động trải nghiệm, hướng nghiệp
• Giáo dục kinh tế và pháp luật

Chủ đề / Chương

Bài học

HOC24

Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng

• Lớp 8
• Toán lớp 8 (Chương trình cũ)
• Hình lăng trụ đứng. Hình chóp đều.

Chủ đề

• Bài 1: Hình hộp chữ nhật
• Bài 2: Hình hộp chữ nhật (Tiếp)
• Bài 3: Thể tích hình hộp chữ nhật
• Bài 4: Hình lăng trụ đứng
• Bài 5: Diện tích xung quanh của hình lăng trụ đứng
• Bài 6: Thể tích của hình lăng trụ đứng
• Bài 7: Hình chóp đều và hình chóp cụt đều
• Bài 8: Diện tích xung quanh của hình chóp đều
• Bài 9: Thể tích hình chóp đều
• Ôn tập chương Hình lăng trụ đứng. Hình chóp đều.

Bài 6: Thể tích của hình lăng trụ đứng

• Lý thuyết
• Trắc nghiệm
• Giải bài tập SGK
• Hỏi đáp
• Đóng góp lý thuyết

1. Công thức tính thể tích

Ở bài trước ta đã biết công thức tính thể tích hình hộp chữ nhật có các kích thước lần lượt là \(a,b,c\) là:

\(V=abc\) hay V = Diện tích đáy x chiều cao

Công thức trên vẫn đúng đối với lăng trụ đứng.

Tổng quát:

Thể tích hình lăng trụ đứng bằng diện tích đáy nhân với chiều cao.

\(V=S.h\)

(\(S\) là diện tích đáy, \(h\) là chiều cao)

@1567239@

2. Các ví dụ

Ví dụ 1: Một lăng trụ đứng có các kích thước được cho như hình vẽ. Tính thể tích của lăng trụ đứng đã cho.

Giải:

Xét đáy tam giác \(ABC\) có: \(AB^2+AC^2=3^2+4^2=25=5^2\)

\(\Rightarrow AB^2+AC^2=BC^2\)

\(\Rightarrow\Delta ABC\) vuông tại \(A\)

Diện tích đáy \(ABC\) là: \(\dfrac{1}{2}.3.4=6\left(cm^2\right)\)

Thể tích hình lăng trụ là: \(6.7=42\left(cm^3\right)\)

Ví dụ 2: Cho một lăng trụ đứng có đáy là hình thoi \(ABCD\) cạnh bằng \(3cm\) và \(\widehat{BAD}=60^0\). Biết chiều cao lăng trụ là 7cm. Tính thể tích hình lăng trụ đứng trên?

Giải:

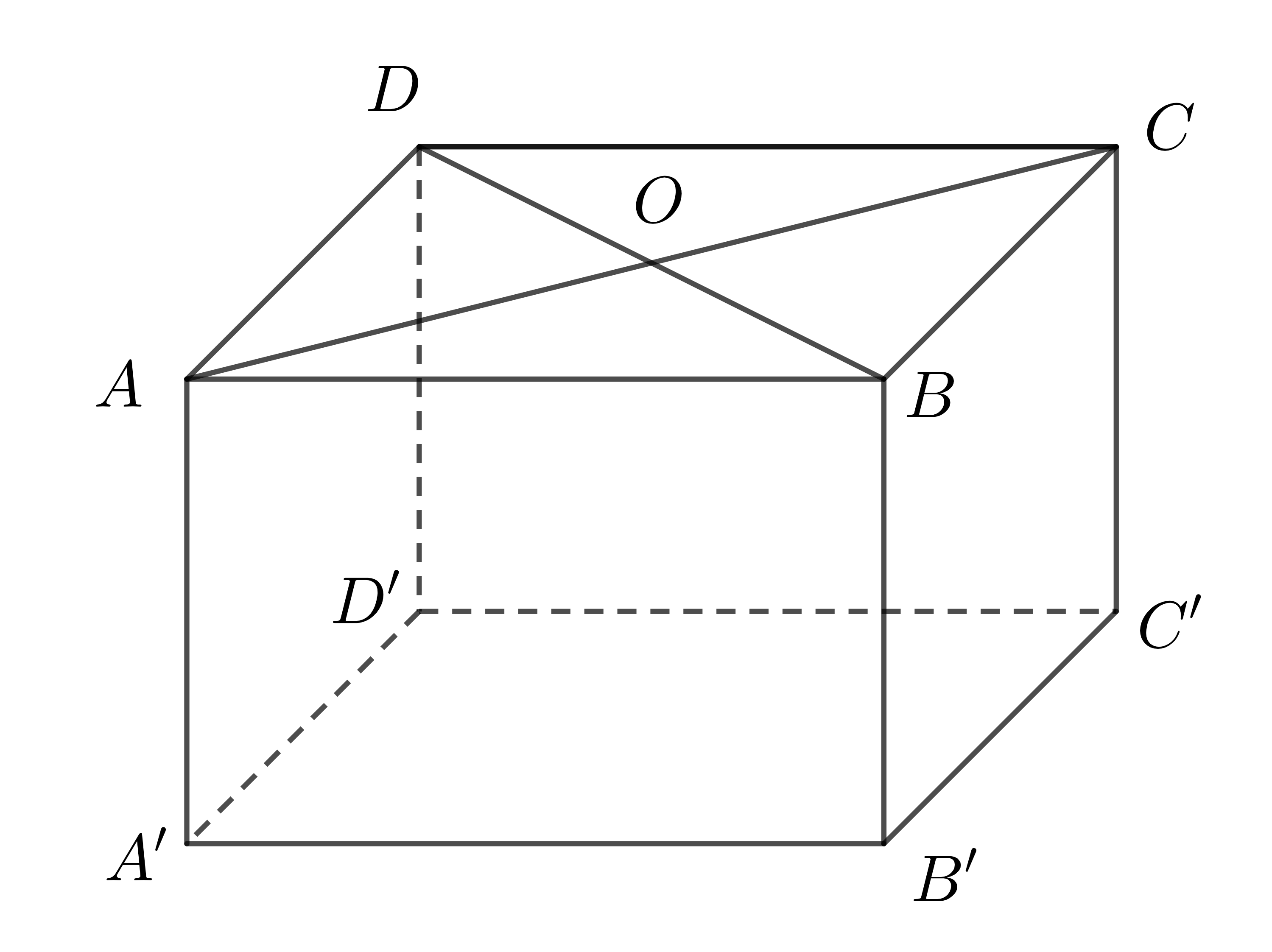
Xét hình thoi \(ABCD\) có \(AB=BC=CD=DA=3cm\)

\(\Rightarrow\Delta BAD\) cân tại \(A\) mà \(\widehat{BAD}=60^0\) \(\Rightarrow\Delta BAD\) đều

\(\Rightarrow BD=3cm\)

Gọi \(O\) là giao điểm 2 đường chéo \(AC,BD\) \(\Rightarrow\) \(O\) là trung điểm mỗi đường và \(AC\perp BD\) tại \(O\)

\(\Rightarrow OB=OD=\dfrac{BD}{2}=1,5\left(cm\right)\)

Xét \(\Delta OAB\) vuông tại \(O\) có \(AB=3cm,OB=1,5cm\)

Áp dụng định lí Py-ta-go ta có: \(OA^2+OB^2=AB^2\)

\(\Rightarrow OA=\sqrt{AB^2-OB^2}=\sqrt{3^2-1,5^2}=\sqrt{6,75}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)

\(\Rightarrow AC=3\sqrt{3}\left(cm\right)\)

Diện tích hình thoi \(ABCD\) là: \(\dfrac{1}{2}.3.3\sqrt{3}=\dfrac{9\sqrt{3}}{2}\) (cm2)

Thể tích hình lăng trụ là: \(7.\dfrac{9\sqrt{3}}{2}=\dfrac{63\sqrt{3}}{2}\approx54,56\left(cm^3\right)\)

Ví dụ 3: Cho hình lăng trụ đứng ngũ giác có các kích thước như hình vẽ (đơn vị: cm). Tính thể tích lăng trụ đã cho.

Giải:

Hình lăng trụ đã cho gồm một hình hộp chữ nhật và một lăng trụ đứng tam giác có cùng chiều cao.

Hình hộp chữ chật có các kích thước là \(4cm,5cm,7cm\)

Thể tích hình hộp chữ nhật là: \(V_1=4.5.7=140\left(cm^3\right)\)

Hình lăng trụ tam giác có đáy là hình một tam giác có cạnh đáy \(5cm\) và đường cao \(2cm\)

Diện tích đáy tam giác là: \(\dfrac{1}{2}.5.2=5\left(cm^2\right)\)

Thể tích lăng trụ tam giác là: \(V_2=5.7=35\left(cm^3\right)\)

Thể tích của hình lăng trụ đã cho là:

\(V=V_1+V_2=140+35=175\left(cm^3\right)\)

Với bài toán này, ta có thể tính riêng diện tích đáy sao đó lấy diện tích đáy nhân với chiều cao như sau:

Diện tích đáy ngũ giác là: \(4.5+\dfrac{1}{2}.5.2=25\left(cm^2\right)\)

Suy ra thể tích hình lăng trụ là: \(V=25.7=175\left(cm^3\right)\)

@1567368@@1567147@

• Lý thuyết
• Trắc nghiệm
• Giải bài tập SGK
• Hỏi đáp
• Đóng góp lý thuyết

Bài trước Bài tiếp theo

Khoá học trên OLM (olm.vn)

• Toán lớp 8 (Kết nối tri thức với cuộc sống)
• Toán lớp 8 (Cánh Diều)
• Toán lớp 8 (Chân trời sáng tạo)
• Ngữ văn lớp 8 (Kết nối tri thức với cuộc sống)
• Ngữ văn lớp 8 (Cánh Diều)
• Ngữ văn lớp 8 (Chân trời sáng tạo)
• Tiếng Anh lớp 8 (i-Learn Smart World)
• Tiếng Anh lớp 8 (Global Success)
• Khoa học tự nhiên lớp 8 (Kết nối tri thức với cuộc sống)
• Khoa học tự nhiên lớp 8 (Cánh diều)
• Khoa học tự nhiên lớp 8 (Chân trời sáng tạo)
• Lịch sử và địa lý lớp 8 (Kết nối tri thức với cuộc sống)
• Lịch sử và địa lý lớp 8 (Cánh diều)
• Lịch sử và địa lý lớp 8 (Chân trời sáng tạo)
• Giáo dục công dân lớp 8 (Kết nối tri thức với cuộc sống)
• Giáo dục công dân lớp 8 (Cánh diều)
• Giáo dục công dân lớp 8 (Chân trời sáng tạo)
• Công nghệ lớp 8 (Kết nối tri thức với cuộc sống)

Khoá học trên OLM (olm.vn)

• Toán lớp 8 (Kết nối tri thức với cuộc sống)
• Toán lớp 8 (Cánh Diều)
• Toán lớp 8 (Chân trời sáng tạo)
• Ngữ văn lớp 8 (Kết nối tri thức với cuộc sống)
• Ngữ văn lớp 8 (Cánh Diều)
• Ngữ văn lớp 8 (Chân trời sáng tạo)
• Tiếng Anh lớp 8 (i-Learn Smart World)
• Tiếng Anh lớp 8 (Global Success)
• Khoa học tự nhiên lớp 8 (Kết nối tri thức với cuộc sống)
• Khoa học tự nhiên lớp 8 (Cánh diều)
• Khoa học tự nhiên lớp 8 (Chân trời sáng tạo)
• Lịch sử và địa lý lớp 8 (Kết nối tri thức với cuộc sống)
• Lịch sử và địa lý lớp 8 (Cánh diều)
• Lịch sử và địa lý lớp 8 (Chân trời sáng tạo)
• Giáo dục công dân lớp 8 (Kết nối tri thức với cuộc sống)
• Giáo dục công dân lớp 8 (Cánh diều)
• Giáo dục công dân lớp 8 (Chân trời sáng tạo)
• Công nghệ lớp 8 (Kết nối tri thức với cuộc sống)

Đóng góp

Lưu lại Lớp học Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Bộ sách Chương trình cũ Hỗ trợ học sinh học sách Cánh Diều Hỗ trợ học sinh học sách Kết nối tri thức với cuộc sống Hỗ trợ học sinh học sách Chân trời sáng tạo Explore English Global Success Friends Plus I-learn Smart World Chủ đề cha Đang tải dữ liệu... Lọc câu hỏi Đang tải dữ liệu... Nội dung