Bài 6 Trang 9 Sgk Toán 8 Tập 2

Lời giải bài 6 trang 9 sgk Toán 8 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 8 bài 2 Phương trình bậc mất một ẩn và cách giải để tự tin hoàn thành tốt các bài tập về phương trình bậc nhất một ẩn khác.

Đề bài 6 trang 9 SGK Toán 8 tập 2

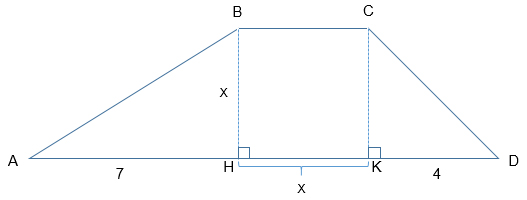
Tính diện tích của hình thang ABCD (h.1) theo x bằng hai cách:

1) Tính theo công thức \(S = BH \times (BC + DA) : 2\)

2) \(S = {S_{ABH}} + {S_{BCKH}} + {S_{CKD}}\)

Sau đó sử dụng giả thiết \(S = 20\) để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

» Bài tập trước: Bài 5 trang 7 SGK Toán 8 tập 2

Giải bài 6 trang 9 sgk Toán 8 tập 2

Hướng dẫn cách làm

Phương trình có dạng \(ax+b=0\), với \(a\) và \(b\) là hai số đã cho và \(a\ne0\), được gọi là phương trình bậc nhất một ẩn.

Bài giải chi tiết

Dưới đây là các cách giải bài 6 trang 9 SGK Toán 8 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

Gọi \(S\) là diện tích hình thang \(ABCD\).

1) Theo công thức

\(S =  \dfrac{BH(BC+DA)}{2}\)

Ta có: \(AD = AH + HK + KD\)

\(\Rightarrow AD = 7 + x + 4 = 11 + x\)

Có \(BH\bot HK, CK\bot HK\) (giả thiết)

Mà \(BC//HK\) (vì \(ABCD\) là hình thang)

Do đó \(BH\bot BC, CK\bot BC\)

Tứ giác \(BCKH\) có bốn góc vuông nên \(BCKH\) là hình chữ nhật

Mặt khác: \(BH=HK=x\) (giả thiết) nên \(BCKH\) là hình vuông

\(\Rightarrow BH = BC =CK=KH= x\)

Thay \(BH=x\)), \(BC=x\), \(DA=11+x\) vào biểu thức tính \(S\) ta được:

\(S = \dfrac{{x\left( {x + 11 + x} \right)}}{2} = \dfrac{{x(11 + 2x)}}{2}\)\(\,=\dfrac{{11x + 2{x^2}}}{2}\)

2) Ta có:

\(\eqalign{ & S = {S_{ABH}} + {S_{BCKH}} + {S_{CKD}} \cr & \,\,\,\,\, = {1 \over 2}BH.AH + BH.HK + {1 \over 2}CK.KD \cr & \,\,\,\,\, = {1 \over 2}x.7 + x.x + {1 \over 2}.x.4 \cr & \,\,\,\,\, = {7 \over 2}x + {x^2} + 2x \cr} \)

Vậy \(S = 20\) ta có hai phương trình:

\(\dfrac{{11x + 2{x^2}}}{2}= 20\)          (1)

\(\dfrac{7}{2}x + x^2+ 2x  = 20 \)       (2)

Cả hai phương trình không có phương trình nào là phương trình bậc nhất.

Giải bài tập khác

Xem thêm hướng dẫn giải các bài tập tiếp theo

• Bài 7 trang 10 sgk Toán 8 tập 2
• Bài 8 trang 10 sgk Toán 8 tập 2

Nội dung trên đã giúp bạn nắm được cách làm và đáp án bài 6 trang 9 sgk toán 8 tập 2. Mong rằng những bài hướng dẫn giải toán 8 của Đọc Tài Liệu sẽ là người đồng hành giúp các bạn học tốt môn học này.