Bài 65 Trang 132 Sách Bài Tập Hình Học Lớp 12 Nâng Cao: Tìm Tập ...

a)Tìm tập hợp các điểm cách đều ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2).. Bài 65 trang 132 Sách bài tập Hình học lớp 12 Nâng cao - Bài 3. Phương trình đường thẳng

a) Tìm tập hợp các điểm cách đều ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2).

b) Tìm quỹ tích các điểm M cách đều hai trục tọa độ Ox, Oy và điểm A(1;1;0).

a) Điểm M(x ; y ; z) cách đều ba điểm A, B, C khi và chỉ khi

      \(\left\{ \matrix{  M{A^2} = M{B^2} \hfill \cr  M{A^2} = M{C^2} \hfill \cr}  \right.\) 

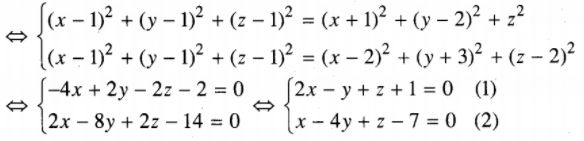
Vậy tập hợp điểm M(x; y; z) là đường thẳng giao tuyến của hai mặt phẳng lần lượt có phương trình (1) và (2). Đường thẳng đó có phương trình là:

                              \(\left\{ \matrix{  x =  - 8 - 3t \hfill \cr  y = t \hfill \cr  z = 15 + 7t \hfill \cr}  \right.\)

Nó chính là trục của đường tròn ngoại tiếp tam giác ABC.

b) Xét điểm M(x ; y ; z). Khi đó khoảng cách dx từ M tới trục Ox là

                  \({d_x} = {{\left| {\left[ {\overrightarrow {OM} ,\overrightarrow i } \right]} \right|} \over {\left| {\overrightarrow i } \right|}} = \sqrt {{y^2} + {z^2}} .\)

khoảng cách dy từ M tới trục Oy là

Advertisements (Quảng cáo)

                  \({d_y} = {{\left| {\left[ {\overrightarrow {OM} ,\overrightarrow j } \right]} \right|} \over {\left| {\overrightarrow j } \right|}} = \sqrt {{x^2} + {z^2}} .\)

Mặt khác \(MA = \sqrt {{{(x - {\rm{ 1}})}^2} + {\rm{ }}{{\left( {y{\rm{ }} - {\rm{ 1}}} \right)}^2} + {\rm{ }}{z^2}.} \)

Vậy M  là một điểm của quỹ tích khi

\(\left\{ \matrix{  {y^2} + {z^2} = {x^2} + {z^2} \hfill \cr  {y^2} + {z^2} = {x^2} + {y^2} + {z^2} - 2(x + y) + 2 \hfill \cr}  \right.\)

\(\Leftrightarrow \left\{ \matrix{  {x^2} = {y^2}  (1) \hfill \cr  {x^2} - 2(x + y) + 2 = 0.   (2) \hfill \cr}  \right.\) 

Từ (1) suy ra x = y hoặc x = -y.

Khi x = y, phương trình (2) có dạng: \({x^2} - 4x + 2 = 0 \Rightarrow x = 2 \pm \sqrt 2 .\)

Trong trường hợp này, quỹ tích M là những điểm (x; y; z) mà:

\(\left\{ \matrix{  x = 2 + \sqrt 2  \hfill \cr  y = 2 + \sqrt 2  \hfill \cr  z = t \hfill \cr}  \right.\)      (3)      và        \(\left\{ \matrix{  x = 2 - \sqrt 2  \hfill \cr  y = 2 - \sqrt 2  \hfill \cr  z = t \hfill \cr}  \right.\)     (4)

Khi \(x =  - y\), phương trình (2) trở thành: \({x^2} + 2 = 0\). Điều này không xảy ra.

Vậy quỹ tích cầm tìm là hai đường thẳng có phương trình (3) và (4)