Bài 7. Phép Vị Tự - Củng Cố Kiến Thức

I. Định nghĩa

Cho điểm O và số $k \ne 0$. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho $\overrightarrow {OM'} = k.\overrightarrow {OM} $ được gọi là phép vị tự tâm O, tỉ số k.

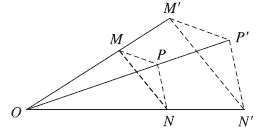
II. Tính chất

* Tính chất 1

Nếu phép vị tự tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M’, N’ thì $\overrightarrow {M'N'} = k.\overrightarrow {MN} $ và $M'N' = \left| k \right|MN$.

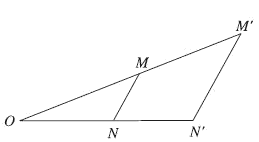
* Tính chất 2

Phép vị tự tỉ số k:

a)Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy

b) Biến đường thảng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

d) Biến đường tròn bán kính R thành đường tròn bán kính $\left| k \right|R$.

III. Tâm tự vị của hai đường tròn

* Định lí

Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia.

* Cách tìm tâm tự vị của hai đường tròn

Cho hai đường tròn $\left( {I;R} \right)$ và $\left( {I';R'} \right)$. Có 3 trường hợp xảy ra:

a) Trường hợp $I$ trùng với ${I'}$

Khi đó phép vị tự tâm $I$ tỉ số $\frac{{R'}}{R}$ và phép vị tự tâm $I$ tỉ số $ - \frac{{R'}}{R}$ biến đường tròn $\left( {I;R} \right)$ thành đường tròn $\left( {I';R'} \right)$.

b) Trường hợp $I$ khác ${I'}$ và $R \ne R'$.

Khi đó phép vị tự tâm O tỉ số $k = \frac{{R'}}{R}$ và phép tự vị tâm ${O_1}$ tỉ số ${k_1} = - \frac{{R'}}{R}$ sẽ biến đường tròn $\left( {I;R} \right)$ thành đường tròn $\left( {I';R'} \right)$. Ta gọi O là tâm vị tự ngoài, còn ${O_1}$ là tâm vị tự trong của hai đường tròn trên.

c) Nếu $I$ khác ${I'}$ và $R = R'$.

Khi đó chỉ có phép vị tự tâm ${O_1}$ tỉ số $k = - \frac{R}{{R'}} = - 1$ biến đường tròn $\left( {I;R} \right)$ thành đường tròn $\left( {I';R'} \right)$. Đó chính là phép đối xứng qua tâm ${O_1}$.