Bài 8: Thể Tích Khối Cầu

I. Lý thuyết Cho khối cầu bán kính R \(V=\frac{4}{3}\pi .R^3\) II. Bài tập Ví dụ 1: Cho hình lập phương ABCD.A'B'C'D'. Tính thể tích khối cầu. a) Ngoại tiếp hình lập phương b) Nội tiếp hình lập phương. Giải

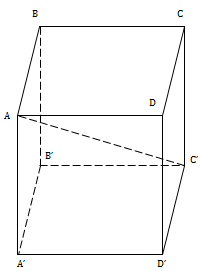
a) Bán kính khối cầu ngoại tiếp hình lập phương là \(R=\frac{1}{2}AC'=\frac{1}{2}\sqrt{a^2+a^2+a^2}=\frac{a\sqrt{3}}{2}\) \(V_1=\frac{4}{3}\pi R^3=\frac{4}{3}\pi .\frac{a^3.3\sqrt{3}}{8}=\frac{a^3\pi .\sqrt{3}}{2}\)(đvtt)

b) Khối cầu nội tiếp hình lập phương có bán kính

\(2r=a\Leftrightarrow r=\frac{a}{2}\) Thể tích khối cầu \(V_2=\frac{4}{3}\pi .r^3=\frac{4}{3}\pi .\frac{a^3}{8}=\frac{\pi a^3}{6}\) (đvtt) ​Ví dụ 2: Thể tích của khối cầu sẽ thay đổi như thế nào nếu. a) Tăng bán kính lên k lần. b) Giảm bán kính k lần.

Giảm a) \(R_1=k.R_2\) \(\frac{V_1}{V_2}=\frac{\frac{4}{3}\pi R^3_1}{\frac{4}{3}.\pi .R^3_2}= \left ( \frac{R_1}{R_2} \right )^3=k^3\) Nếu tăng bán kính lên k lần thì thể tích khối cầu tăng gấp k3 lần. b) \(R_1=\frac{1}{k}.R_2\) \(\frac{V_1}{V_2}=\frac{\frac{4}{3}\pi .R^3_1}{\frac{4}{3}\pi .R^3_2}= \left ( \frac{R_1}{R_2} \right )^3=\frac{1}{k^3}\) Nếu giảm bán kính k lần thì thể tích khối cầu giảm k3 lần. Ví dụ 3: Cho hình chóp S.ABC có \(SA\perp (ABC), AB=a, AC=b,\widehat{BAC}=60^0\). H, K l3 h/c của A trên SB, SC. a) CMR: 5 điểm A, B, C, H, K cùng thuộc một mặt cầu. b) Tính thể tích khối cầu đó. Giải

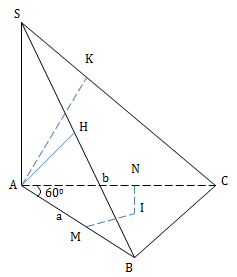
a) Gọi M, N lần lượt là trung điểm AB, AC Kẻ đường trung trực Mx của cạnh AB trong (ABC) Ta có (SAB) \(\perp\) (ABC), có giao tuyến là AB nên Mx \(\perp\) (SAB) hay Mx \(\perp\) (AHB) Vậy Mx là trục đường tròn ngoại tiếp tam giác AHB Tương tự kẻ Ny là đường trung trực của cạnh AC trong tam giác (ABC) ta có Ny là trục đường tròn ngoại tiếp tam giác AKC Trong (ABC) \(Mx\cap Ny=I\) I là tâm đường tròn ngoại tiếp tam giác ABC \(\left.\begin{matrix} I\in Mx\Rightarrow IA=IH=IB\\ I\in Ny\Rightarrow IA=IK=IC \end{matrix}\right\}\) 5 điểm A, B, C, H, K cùng thuộc mặt cầu tâm I b)

R = IA Trong tam giác ABC \(BC^2=AB^2+AC^2-2AB.AC.cos60^0=a^2+b^2-ab\) \(R=\frac{BC}{2 sin\widehat{A}}=\frac{\sqrt{a^2+b^2-ab}}{2.\frac{\sqrt{3}}{2}} =\sqrt{\frac{a^2+b^2-ab}{3}}\) \(V=\frac{4}{3}.\pi .R^3=\frac{4}{3}.\pi \frac{a^2+b^2-ab}{3}.\sqrt{\frac{a^2+b^2-ab}{3}}\)