Bài 9: Bài Toán Tìm GTLN, GTNN Của Hàm Số

1. Lý thuyết

a) M được gọi là GTLN f(x) trên D nếu \(\left\{\begin{matrix} f(x)\leq M\\ \exists x_0, f(x_0)=M \end{matrix}\right.\) m=GTNN f(x) nếu \(\left\{\begin{matrix} m\leq f(x), \forall x\in D\\ \forall x_0\in D, f(x_0)=m \end{matrix}\right.\)

b) Bài toán 1

Tìm GTLN, NN trên D

+ Lập BBT trên D

+ Từ BBT suy ra KL

Bài toán 2 Tìm GTLN, NN trên [a;b] + Tìm nghiệm f'(x) =0 trên [a;b] giả sử x1, x2 \(\begin{matrix} GTLN f(x) = GTLN f(x) \\ [a;b] \ \ \ \ \ \ [a;b] \end{matrix}\left\{\begin{matrix} f(a), f(b), f(x_1)...f(x_n) \\ \end{matrix}\right.\) \(\begin{matrix} GTNN f(x) = GTNN f(x) \\ [a;b] \ \ \ \ \ \ [a;b] \end{matrix}\left\{\begin{matrix} f(a), f(b), f(x_1)...f(x_n) \\ \end{matrix}\right.\) 2. Bài tập VD1: Tìm GTLN, NN của \(f(x)=x^3-3x\) trên [-2;3] Giải \(f'(x)=3x^2-3\) \(f'(x)=0\Leftrightarrow \begin{bmatrix} x=1\\ x=-1 \end{matrix}\)

f(-2) = -2

f(1) = -1

f(3) = 18

f(-1) = 2 \(\underset{[-2;3]}{GTLN} f(x) = 18\) khi x= 3 \(\underset{[-2;3]}{GTNN} f(x) = -2 \ khi \ \bigg \lbrack\begin{matrix} x=-2\\ x=1 \end{matrix}\)

VD2: Tìm GTNN của \(f(x)=x+\frac{1}{x}\) trên \([2;+\infty )\) Giải \(f'(x)=1-\frac{1}{x^2}=\frac{x^2-1}{x^2}\) \(f'(x)=0\Leftrightarrow x^2-1=0\) \(\Leftrightarrow \bigg \lbrack\begin{matrix} x=1\notin [2;+\infty )\\ x=-1\notin [2;+\infty ) \end{matrix}\) 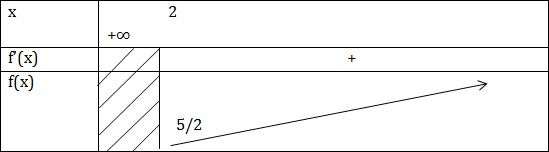\(\underset{[2;+\infty ]}{GTNN} f(x) = \frac{5}{2} \ khi \ x = 2\) VD3: Tìm GTLN của \(f(x)=\sqrt{x}+\sqrt{2-x}\) TXĐ: [0;2] \(f'(x)=\frac{1}{2\sqrt{x}}-\frac{1}{2\sqrt{2-x}}\) \(f'(x)=0\Leftrightarrow \sqrt{x}-\sqrt{2-x}\Leftrightarrow x=1\) \(f(0)=\sqrt{2}\) \(f(x)=\sqrt{2}\) \(f(1)=\sqrt{2}\) \(\underset{[0;2]}{GTLN}f(x)=2 \ khi \ x=1\) \(\underset{[0;2]}{GTLN}f(x)=\sqrt{2} \ khi \ \left\{\begin{matrix} x=0\\ x=2 \end{matrix}\right.\) VD4: Tìm GTNN của hàm số \(f(x)=sin^3x-3sin^2x\) Giải Đặt t = sinx \(t \in [-1;1]\) Bài toán trở thành tìm GTLN, GTNN của \(g(t)=t^3-3t^2\) trên [-1;1] \(g'(t)=3t^2-6t\) \(g'(t)=0\Leftrightarrow 3t(t-2)=0\) \(\Leftrightarrow \bigg \lbrack\begin{matrix} t=0\\ t=2\notin [-1;1] \end{matrix}\) g(0) = 0 g(-1) = -4, g(1) =-2 \(\underset{[-1;1]}{GTLN}g(t)=0 \ khi \ t=0\) \(\Leftrightarrow sinx=0\Leftrightarrow x=k\pi (k\in z)\) \(\underset{[-1;1]}{GTNN}g(t)=-4 \ khi \ t =1\) \(\Leftrightarrow sinx=-1\Leftrightarrow x=-\frac{\pi}{2}+k2\pi\) KL: GTLN f(x) = 0 khi \(x=k\pi\) GTNN f(x) = -4 khi \(x=-\frac{\pi}{2}+k2\pi\) VD5: Tìm GTLN của hàm số \(f(x)=\frac{x+3}{\sqrt{x^2+1}}\) Giải \(f'(x)=\frac{\sqrt{x^2+1}-\frac{2x(x+3)}{2\sqrt{x^2+1}}}{x^2+1}\) \(=\frac{x^2+1-x^2-3x}{(x^2+1)\sqrt{x^2+1}}\) \(=\frac{1-3x}{(x^2+1)\sqrt{x^2+1}}\) \(f'(x)=0\Leftrightarrow 1-3x=0\) \(\Leftrightarrow x=\frac{1}{3}\) 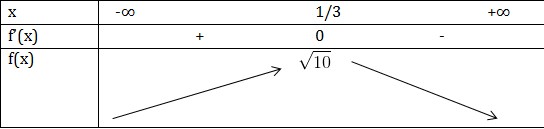\(GTLN f(x)=\sqrt{10} \ khi \ x = \frac{1}{3}\) Khai thác bt: \(\frac{x+3}{\sqrt{x^2+1}}\leq \sqrt{10}\Rightarrow \frac{1}{\sqrt{10}}(x+3)\leq \sqrt{x^2+1}\) BT cho x + y + z = 1. Tìm \(GTNN T=\sqrt{x^2+1}+\sqrt{y^2+1}+\sqrt{z^2+1}\)