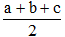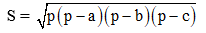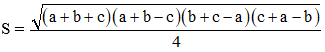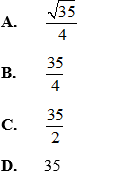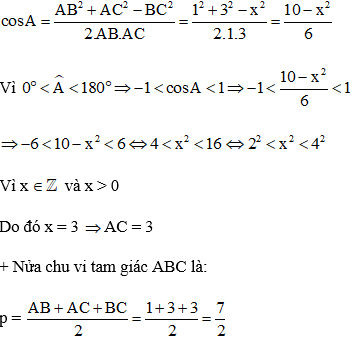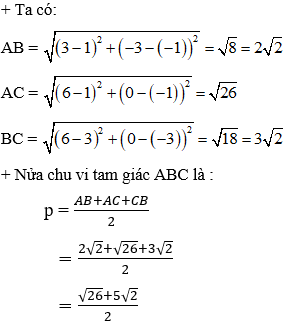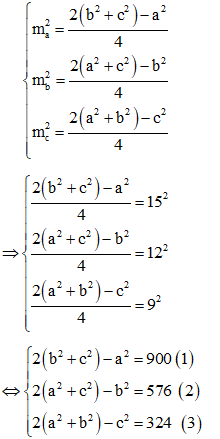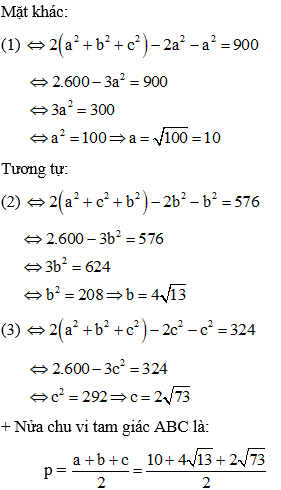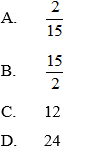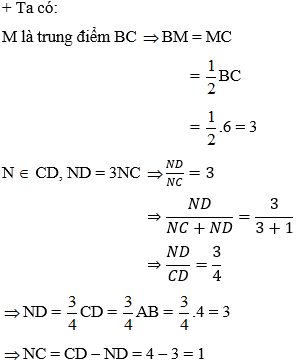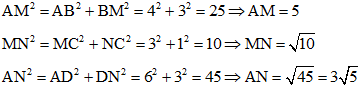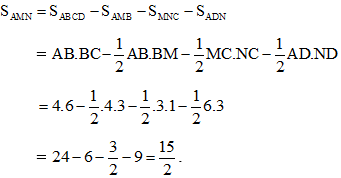Bài Tập Công Thức Heron Tính Diện Tích Tam Giác ...

A. Phương pháp giải

• Công thức Hê – rông dùng để tính diện tích của một tam giác khi biết ba cạnh của tam giác.

• Nội dung công thức Hê – rông:

Cho tam giác ABC có 3 cạnh BC = a, CA = b và AB = c

Gọi p là nửa chu vi tam giác ABC:

 p =

Khi đó ta có diện tích tam giác ABC:

 

Ngoài ra, công thức Hê – rông còn được viết dưới dạng sau:

 

• Phương pháp tìm diện tích tam giác sử dụng công thức Hê – rông:

Bước 1: Tính độ dài các cạnh của tam giác (nếu chưa có)

Bước 2: Tính nửa chu vi tam giác

Bước 3: Tính diện tích tam giác theo công thức Hê – rông.

B. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC có AB = 1, AC = 3. Biết độ dài cạnh BC là một số nguyên. Diện tích của tam giác ABC.

Hướng dẫn giải:

+ Gọi BC = x > 0, x ∈Z

Áp dụng hệ quả định lý Cô – sin trong tam giác ABC, ta có:

Đáp án A

Ví dụ 2: Cho tam giác ABC có tạo độ 3 đỉnh A(1;-1), B(3;-3), C(6;0). Tính diện tích tam giác ABC.

Hướng dẫn giải:

Vậy diện tích tam giác ABC là 6 đvdt.

Ví dụ 3: Cho tam giác ABC có độ dài các đường trung tuyến ma = 15, mb = 12, mc = 9. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Gọi BC = a, AC = b, AB = c

Áp dụng công thức trung tuyến ta có:

Lấy (1) + (2) + (3), cộng vế theo vế ta được

2(b2 + c2) - a2 + 2(a2 + c2) - b2 + 2 (a2 + b2) - c2 = 900 + 576 + 324

⇔ (2b2 - b2 + 2b2) + (2c2 + 2c2 - c2) + (-a2 + 2a2 + 2a2) = 1800

⇔ 3b2 + 3c2 + 3a2 = 1800

⇔ 3(a2 + b2 + c2) = 1800

⇔ a2 + b2 + c2 = 600

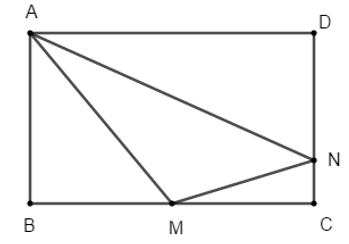
Ví dụ 4: Cho hình chữ nhật ABCD có AB = 4 và BC = 6. Gọi trung điểm của BC là M, N là một điểm trên cạnh CD sao cho ND = 3NC. Diện tích tam giác AMN là:

Hướng dẫn giải:

Áp dụng định lý Pyatgo cho các tam giác vuông ABM, MNC và AND ta có:

Theo công thức Hê – rông diện tích tam giác AMN là:

+ Ngoài ra, chúng ta có thể tính diện tích tam giác AMN bằng cách sau:

Đáp án B

Ví dụ 5: Cho tam giác ABC có BC = 9, CA = 6, AB = 5. Tính diện tích tam giác ABC.

Hướng dẫn giải: