Bài Tập GTLN - GTNN Của Số Phức - Tài Liệu ôn Tập Môn Toán Lớp 12

Download.vn Hướng dẫn sử dụng, mẹo vặt, thủ thuật phần mềm tài liệu và học tập Thông báo Mới

• Tất cả
  • Học tập
  • Tài liệu
  • Hướng dẫn
• • Học tập
  • Tài liệu
  • Hướng dẫn
  • Đề thi
  • Học tiếng Anh
  • Giáo án
  • Bài giảng điện tử
  • Tài liệu Giáo viên
  • Tập huấn Giáo viên

Gói Thành viên của bạn sắp hết hạn. Vui lòng gia hạn ngay để việc sử dụng không bị gián đoạn Download.vn Học tập Lớp 12 Toán 12 Bài tập GTLN - GTNN của Số Phức Tài liệu ôn tập môn Toán lớp 12 Tải về Bình luận

• 1

Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo

Tìm hiểu thêm » Mua Pro 79.000đ Hỗ trợ qua Zalo

Với mong muốn đem đến cho các bạn đọc có thêm nhiều tài liệu học tập môn Toán lớp 12, Download.vn giới thiệu Bài tập GTLN - GTNN của Số phức.

Bài tập giá trị lớn nhất và giá trị nhỏ nhất (viết tắt là GTLN – GTNN hoặc min – max) của biểu thức số phức là một dạng toán vận dụng cao thường gặp trong các đề thi thử THPT Quốc gia môn Toán trong những năm gần đây. Đây là dạng toán ít được đề cập đến trong sách giáo khoa Giải tích 12, do đó đã gây không ít bỡ ngỡ và khó khăn cho các bạn học sinh trong quá trình tiếp cận và tìm hướng giải quyết bài toán. Nội dung chi tiết mời các bạn cùng tham khảo và tải tại đây.

Bài tập GTLN - GTNN của Số Phức

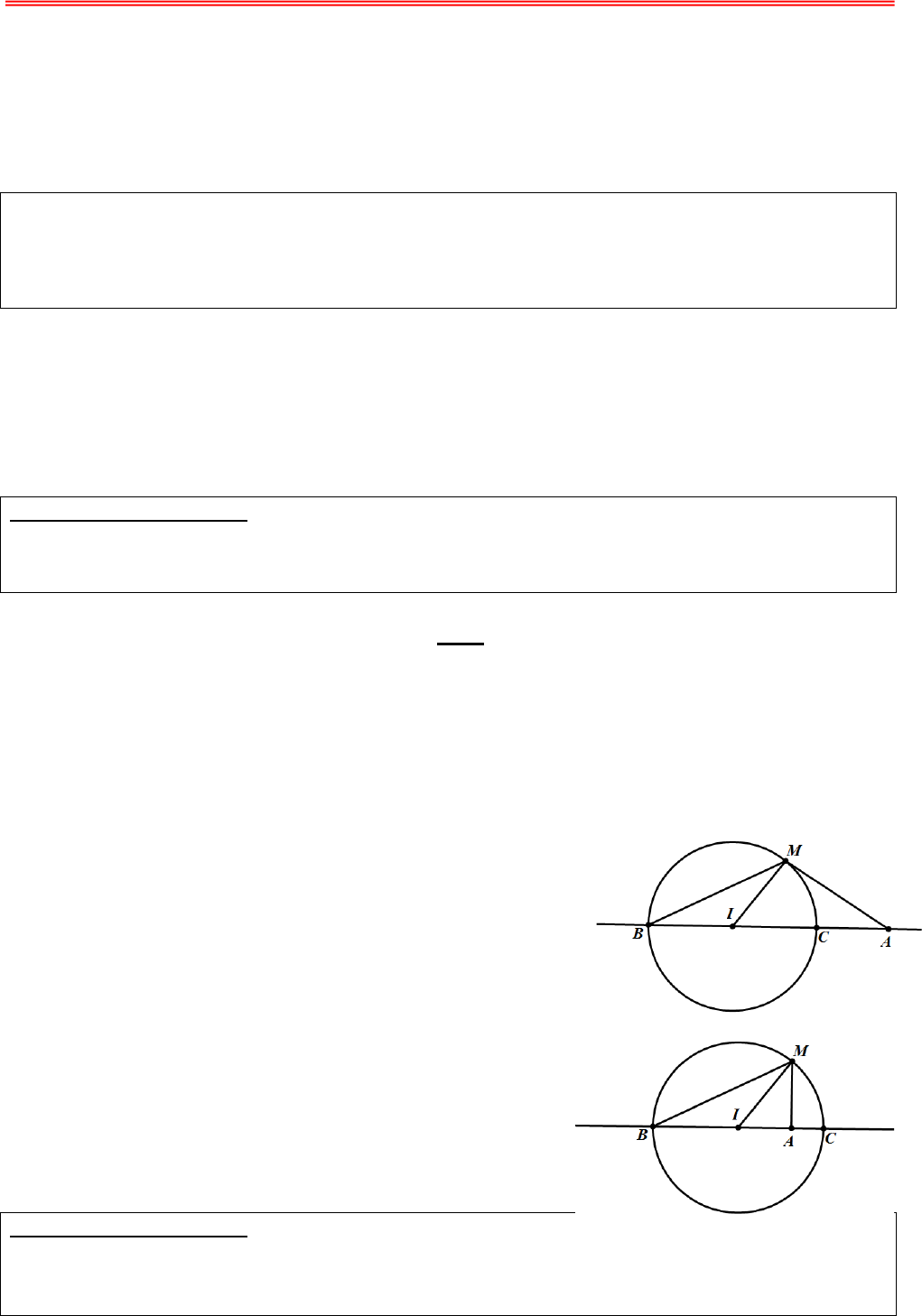https://toanmath.com/GTLN - GTNN CỦA MÔĐUN SỐ PHỨCA. BÀI TOÁN CỰC TRỊ CỦA SỐ PHỨCI. CÁC BÀI TOÁN QUI VỀBÀI TOÁN TÌM GIÁ TRỊ LỚN NHẤT, NHỎNHẤT CỦA HÀMMỘT BIẾN1. PHƯƠNG PHÁPBài toán: Trong các số phức z thoả mãn điều kiện T. Tìm số phức z để biểu thức P đạt giá trị nhỏ nhất, lớn nhất Từ điều kiện T, biến đổi để tìm cách rút ẩn rồi thế vào biểu thức P đểđược hàm một biến. Tìm giá trị lớn nhất (hoặc nhỏ nhất) tuỳ theo yêu cầu bài toán của hàm số một biến vừa tìm được.II. CÁC BÀI TOÁN QUI VỀBÀI TOÁN TÌM GIÁ TRỊ LỚN NHẤT, NHỎNHẤT CỦA MỘTBIỂU THỨC HAI BIẾN MÀ CÁC BIẾN THOẢMÃN ĐIỀU KIỆN CHO TRƯỚC.1. PHƯƠNG PHÁP:Để giải được lớp bài toán này, chúng tôi cung cấp cho học sinh các bất đẳng thức cơ bản như: Bất đẳngthức liên hệ giữa trung bình cộng và trung bình nhân, bất đẳng thức Bunhia- Cốpxki, bất đẳng thức hìnhhọc và một số bài toán công cụ sau:UBÀI TOÁN CÔNG CỤ 1:U Cho đường tròn ()T cố định có tâm I bán kính R và điểm A cố định. Điểm M di động trên đường tròn ()T. Hãy xác định vịtrí điểm M sao cho AM lớn nhất, nhỏ nhất.UGiải:TH1: A thuộc đường tròn (T) Ta có: AM đạt giá trị nhỏ nhất bằng 0 khi M trùng với A AM đạt giá trị lớn nhất bằng 2R khi M là điểm đối xứng với A qua I TH2: A không thuộc đường tròn (T) Gọi B, C là giao điểm của đường thẳng qua A,I và đường tròn (T); Giả sử AB < AC. +) Nếu A nằm ngoài đường tròn (T) thì với điểm M bất kì trên (T), ta có:AMAIIMAIIBAB≥−=−=. Đẳng thức xảy ra khi MB≡ AMAIIMAIICAC≤+=+=. Đẳng thức xảy ra khi MC≡+) Nếu A nằm trong đường tròn (T) thì với điểm M bất kì trên (T), ta có:AMIMIAIBIAAB≥−=−=. Đẳng thức xảy ra khi MB≡ AMAIIMAIICAC≤+=+=. Đẳng thức xảy ra khi MC≡ Vậy khi M trùng với B thì AM đạt gía trị nhỏ nhất. Vậy khi M trùng với C thì AM đạt gía trị lớn nhất. UBÀI TOÁN CÔNG CỤ 2:U Cho hai đường tròn 1()T có tâm I, bán kính RR1R; đường tròn 2()T có tâm J, bán kính RR2R. Tìm vị trí của điểm M trên 1()T, điểm N trên 2()T sao cho MN đạt giá trị lớn nhất, nhỏ nhất. 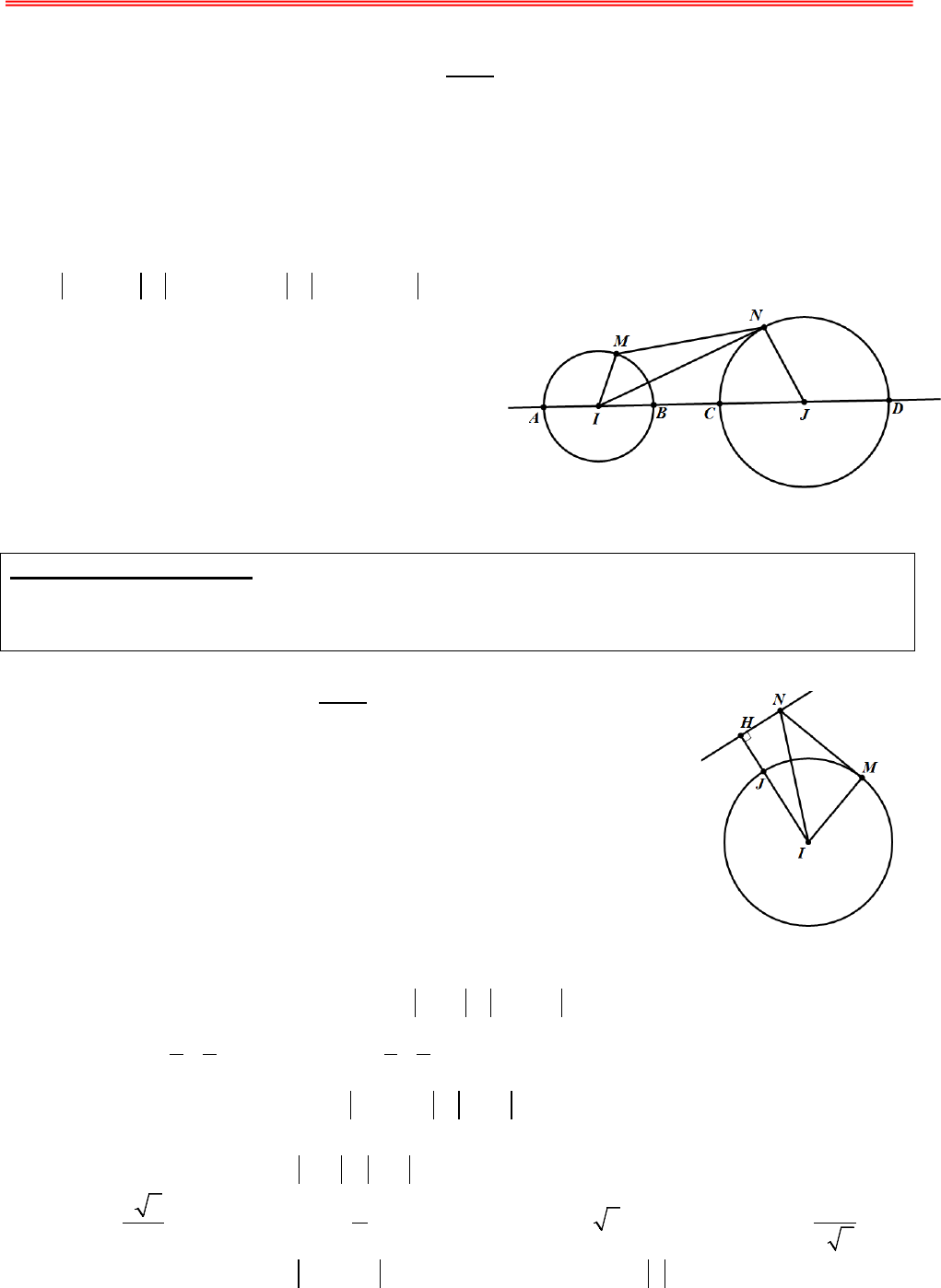https://toanmath.com/ UGiải:Gọi d là đường thẳng đi qua I, J; d cắt đường tròn 1()T tại hai điểm phân biệt A, B (giả sử JA > JB) ; d cắt 2()T tại hai điểm phân biệt C, D ( giả sử ID > IC). Với điểm M bất khì trên 1()T và điểm N bất kì trên 2()T. Ta có: 12MNIMINIMIJJNRRIJAD≤+≤++=++=. Đẳng thức xảy ra khi M trùng với A và N trùng với D12MNIMINIJIMJNIJRRBC≥−≥−−=−+=. Đẳng thức xảy ra khi M trùng với B và N trùng với C. Vậy khi M trùng với A và N trùng với D thì MN đạt giá trị lớn nhất. khi M trùng với B và N trùng với C thì MN đạt giá trị nhỏ nhất. UBÀI TOÁN CÔNG CỤ 3:U Cho hai đường tròn ()T có tâm I, bán kính R; đường thẳng ∆ không có điểm chung với ()T. Tìm vịtrí của điểm M trên ()T, điểm N trên ∆ sao cho MN đạt giá trị nhỏ nhất. UGiải:Gọi H là hình chiếu vuông góc của I trên d Đoạn IH cắt đường tròn ()T tại J Với M thuộc đường thẳng ∆, N thuộc đường tròn ()T, ta có: MNINIMIHIJJHconst≥−≥−==. Đẳng thức xảy ra khi ;MHNI≡≡ Vậy khi M trùng với H; N trùng với J thì MN đạt giá trị nhỏ nhất. B – BÀI TẬP Câu 1. Trong các số phức thỏa mãn điều kiện 32.zizi+=+− Tìm số phức có môđun nhỏ nhất? A. 1255zi=−+. B. 1255zi=−. C. 12zi=−+. D. 12zi=−.Câu 2. Trong các số phức z thỏa mãn 242zizi−−=−. Số phức z có môđun nhỏ nhất là A. 32zi=+ B. 1zi=−+ C. 22zi=−+ D. 22zi=+ Câu 3. Cho số phức z thỏa mãn 1−=−zzi. Tìm mô đun nhỏ nhất của số phứcw22=+−zi. A. 322. B. 32. C. 32. D. 322.Câu 4. Cho số phức z thỏa mãn 341zi−−=. Tìm giá trị nhỏ nhất của z. A. 6. B. 4. C. 3. D. 5. 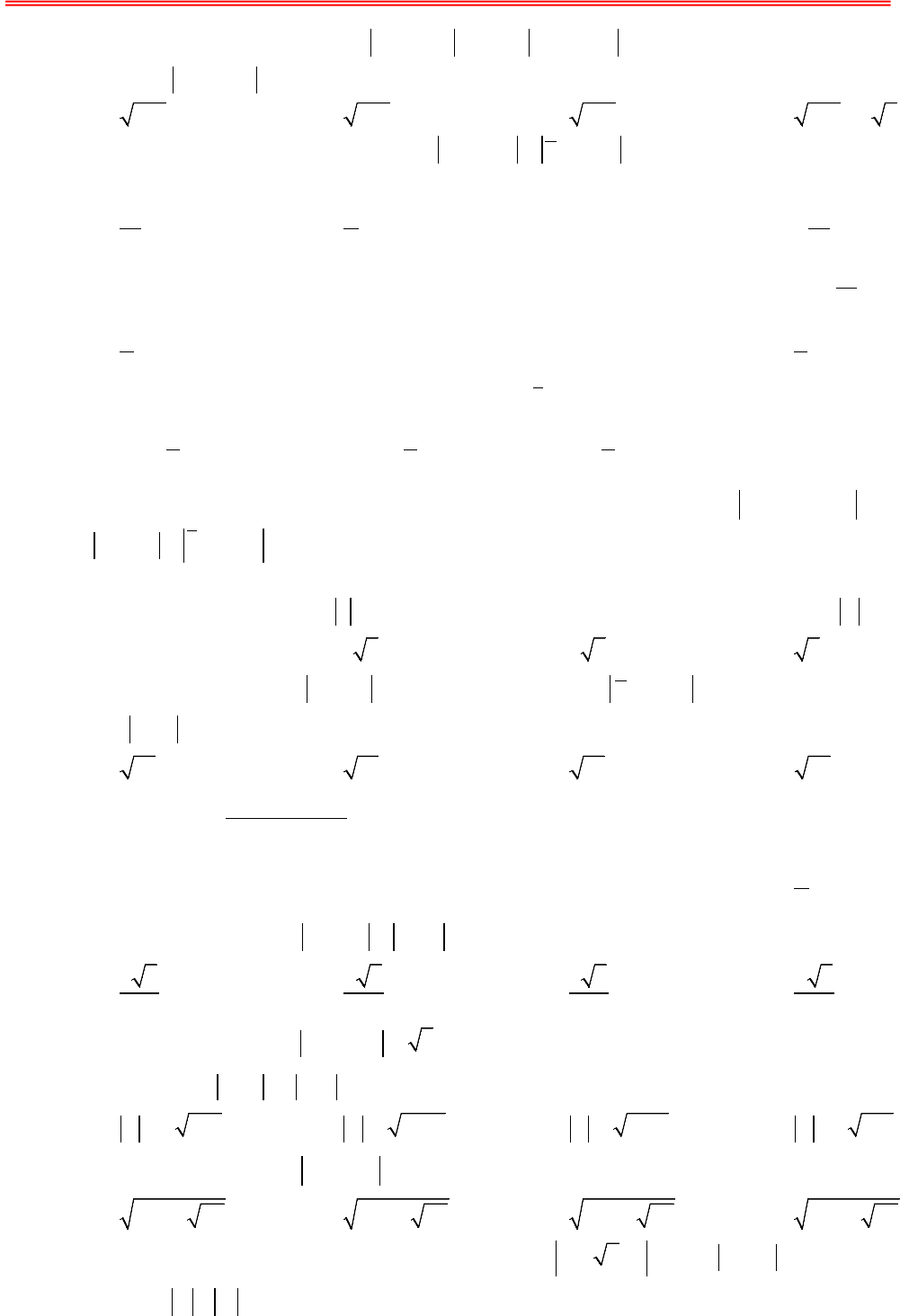https://toanmath.com/ Câu 5. Cho hai số phức 1z, 2z thỏa mãn 1352zi−+= và 2124izi−+=. Tìm giá trị lớn nhất của biểu thức 1223Tizz=+. A. 31316+. B. 313. C. 3138+. D. 31325+.Câu 6. Trong các số phức z thỏa mãn điều kiện 2312zizi+−=+−, hãy tìm phần ảo của số phức có môđun nhỏ nhất? A. 1013. B. 25. C. 2−. D. 213−.Câu 7. Xét các số phức 134zi=− và 22zmi=+, ()m∈. Giá trị nhỏ nhất của môđun số phức 21zz bằng? A. 25. B. 2. C. 3. D. 15.Câu 8. Số phức z nào sau đây có môđun nhỏ nhất thỏa |||34|zzi=−+ : A. 322zi=−−. B. 738zi=−. C. 322zi=+. D. 3–4zi=−.Câu 9. Có tất cả bao nhiêu giá trị nguyên của m để có đúng hai số phức z thỏa mãn ()18zmi−−+= và 123zizi−+=−+. A. 66. B. 130. C. 131. D. 63.Câu 10. Cho các số phức z thoả mãn 2=z. Đặt ()1212=+−+wizi. Tìm giá trị nhỏ nhất của w. A. 2. B. 35. C. 25. D. 5.Câu 11. Cho số phức z thỏa mãn 11zi−−=, số phức w thỏa mãn 232wi−−=. Tìm giá trị nhỏ nhất của zw−. A. 173+ B. 133+ C. 133− D. 173− Câu 12. Cho số phức (),12mizmmmi−+=∈−−. Tìm môđun lớn nhất của .z A. 2. B. 1. C. 0. D. 12.Câu 13. Cho số phức z thỏa mãn 13zizi+−=−. Tính môđun nhỏ nhất của zi−. A. 3510. B. 455. C. 355. D. 7510. Câu 14. Cho số phức z thoả mãn 345zi−−=. Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 222Pzzi=+−−. Tính môđun của số phức .wMmi=+ A. 2309w=. B. 2315w=. C. 1258w=. D. 3137w=.Câu 15. Cho số phức z thỏa mãn 123zi−+=. Tìm môđun lớn nhất của số phức 2.zi− A. +26817. B. −26417. C. +26617. D. −26617.Câu 16. Giả sử1z,2z là hai trong số các số phức zthỏa mãn 21izi+−= và 122zz−=. Giá trị lớn nhất của 12zz+ bằng Chia sẻ bởi: Trịnh Thị Thanh

Tải về

Liên kết tải về Bài tập GTLN - GTNN của Số Phức 1,4 MB Tải về Tìm thêm: Toán 12

Tài liệu tham khảo khác

• Bài tập trắc nghiệm biểu diễn hình học của số phức

Có thể bạn quan tâm

• 

  Phân tích đánh giá chủ đề và những nét đặc sắc về nghệ thuật của truyện Con chó xấu xí

  10.000+
• 

  Chuyên đề giá trị tuyệt đối môn Toán lớp 7

  10.000+
• 

  Bộ đề thi học kì 2 môn Tin học lớp 9 năm 2024 - 2025 (Sách mới)

  50.000+ 1
• 

  Bài giảng Kinh tế học vi mô - Tài liệu học môn kinh tế học vi mô

  50.000+
• 

  Tả con voi trong vườn thú - 4 Dàn ý & 19 bài văn tả con voi lớp 4

  100.000+ 19
• 

  Văn mẫu lớp 9: Phân tích chi tiết vết sẹo trong truyện Chiếc lược ngà

  50.000+
• 

  Viết một đoạn văn tả cảnh biển (54 mẫu)

  100.000+ 1
• 

  Cách thay thế từ/cụm từ trong bài nghị luận văn học

  100.000+ 2
• 

  Kế hoạch dạy học môn Tiếng Anh Tiểu học năm 2024 - 2025

  10.000+
• 

  Văn mẫu lớp 11: Nghị luận về giới hạn trong cuộc sống (2 Dàn ý + 10 mẫu)

  100.000+

Xem thêm

Nhiều người đang xem

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng! Xác thực ngay Số điện thoại này đã được xác thực! Bạn có thể dùng Sđt này đăng nhập tại đây! Lỗi gửi SMS, liên hệ Admin Sắp xếp theo Mặc định Mới nhất Cũ nhất Xóa Đăng nhập để Gửi KHO TÀI LIỆU GIÁO DỤC & HỖ TRỢ CAO CẤP

Hỗ trợ tư vấn

Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu

Hotline

024 322 333 96

Khiếu nại & Hoàn tiền

Giải quyết vấn đề đơn hàng & hoàn trả

Mới nhất trong tuần

• Sơ đồ tư duy môn Toán 12 (Cả năm, Chương trình mới)

  

• Các dạng bài tập cực trị của hàm số

  

• Tài liệu ôn thi Toán lớp 12

  

• Bộ đề thi chọn học sinh giỏi môn Toán lớp 12 (Cấu trúc mới)

  

• Tóm tắt lý thuyết và giải nhanh Toán 12

  

• Các dạng bài tập tính đơn điệu của hàm số

  

• Đề thi thử THPT Quốc gia năm 2025 môn Ngữ văn trường THPT Yên Dũng 2, Bắc Giang

  

• 524 câu hỏi vận dụng cao trong các đề thi THPT Quốc gia

  

• Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 12 năm 2023 - 2024

  

• Lý thuyết và bài tập trắc nghiệm số phức

  

Đóng Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm Mua Download Pro 79.000đ Nhắn tin Zalo

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Phường Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: [email protected]. Bản quyền © 2025 download.vn.