Bài Tập Toán Lớp 10 Chương 2: Hàm Số Bậc Nhất - Bậc Hai

Bài tập Toán lớp 10 chương 2: Hàm số bậc nhất - bậc hai Toán 10 chương 2: Hàm số Bài trước Tải về Bài sau Lớp: Lớp 10 Môn: Toán Loại File: Word + PDF Phân loại: Tài liệu Tính phí

Nâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi.

Tìm hiểu thêm » Mua ngay Từ 79.000đ Hỗ trợ Zalo

Bài tập Đại số lớp 10 chương 2

Bài tập Toán lớp 10 chương 2: Hàm số bậc nhất - bậc hai bao gồm các bài tập Toán lớp 10 cơ bản về hàm số, hàm số bậc nhất, hàm số bậc 2, giúp các bạn học tốt hơn. Bên cạnh đó, tài liệu cũng hữu ích với các thầy cô giáo trong việc ôn tập trọng tâm cho học sinh để đạt hiệu quả cao hơn trong môn học này.

• Bài tập mệnh đề toán học lớp 10
• Bài tập Toán lớp 10 chương 1: Mệnh đề - Tập hợp
• Bảng công thức lượng giác dùng cho lớp 10 - 11 - 12
• Bài tập Toán lớp 11: Đạo hàm
• Tóm tắt toàn bộ lý thuyết và công thức Hình học 11

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 10, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 10 sau: Nhóm Tài liệu học tập lớp 10. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

HÀM SỐ

Bài 1. Tìm tập xác định của hàm số y = f(x):

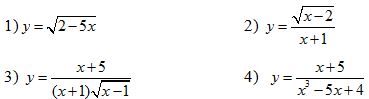
Hướng dẫn giải

a. \(y=\sqrt{2-5x}\)

Điều kiện xác định: 

\(2-5x\ge 0\Rightarrow x\le \frac{5}{2}\)

Vậy tập xác định của hàm số là: \(D=\mathbb{R}\backslash \left( \frac{5}{2},+\infty \right)\)

b. \(y=\dfrac{\sqrt{x-2}}{x+1}\)

Điều kiện xác định: \(\left\{ \begin{matrix} x-2\ge 0 \\ x+1\ne 0 \\ \end{matrix}\Leftrightarrow \left\{ \begin{matrix} x\ge 2 \\ x\ne -1 \\ \end{matrix} \right. \right.\Rightarrow x\ge 2\)

Vậy tập xác định của hàm số là: \(D=\mathbb{R}\backslash (-\infty ,2)\)

c. \(y=\frac{x+5}{\left( x+1 \right)\sqrt{x-1}}\)

Điều kiện xác định: \(\left\{ \begin{matrix} x+1\ne 0 \\ x-1\ge 0 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x\ne -1 \\ x\ge 1 \\ \end{matrix} \right.\Rightarrow x\ge 1\)

Vậy tập xác định của hàm số là \(D=\mathbb{R}\backslash (-\infty ,1)\)

d. \(y=\frac{x+5}{{{x}^{2}}-5x+4}\)

Điều kiện xác định của hàm số là: \({{x}^{2}}-5x+4\ne 0\Rightarrow x\ne 4,x\ne 1\)

Vậy tập xác định của hàm số là: \(D=\mathbb{R}\backslash \left\{ 1,4 \right\}\)

Bài 2. Tìm tập xác định của hàm số y = f(x):

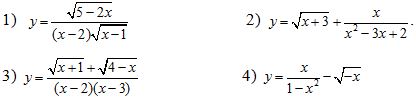
Hướng dẫn giải

a. \(y=\frac{\sqrt{5-2x}}{\left( x-2 \right)\sqrt{x-1}}\)

Điều kiện xác định của hàm số:

\(\left\{ \begin{matrix} 5-2x\ge 0 \\ x-2\ne 0 \\ x-1\ge 0 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x\le \dfrac{5}{2} \\ x\ne 2 \\ x\ge 1 \\ \end{matrix} \right.\)

Vậy tập xác định của hàm số là: \(D=\left[ 1,\frac{5}{2} \right]\backslash \left\{ 2 \right\}\)

b. \(y=\sqrt{x+3}+\frac{x}{{{x}^{2}}-3x+2}\)

Điều kiện xác định của hàm số:

\(\left\{ \begin{matrix} x+3\ge 0 \\ {{x}^{2}}-3x+2\ne 0 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} x\ge -3 \\ x\ne 2,x\ne 1 \\ \end{matrix} \right.\)

Vậy tập xác định của hàm số là: \(D=\mathbb{R}\backslash \left( -\infty ,-3 \right)\cup \left\{ 2,1 \right\}\)

Bài 3. Tìm tập xác định của hàm số y = f(x):

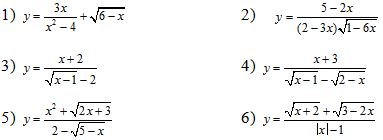
Bài 4.

a) Tìm a để hàm số có tập xác định là R.

b) Hàm số: có TXĐ là R.

Hướng dẫn giải

a. Điều kiện xác định của hàm số: \(x^2-6x+a-2\neq0\)

Để hàm số có tập xác định \(\mathbb{R}\) thì phương trình \(x^2-6x+a-2=0\) vô nghiệm