Bài Tập Về Trường Hợp Bằng Nhau Thứ Nhất Của Tam Giác Cạnh

01 Đề bài:

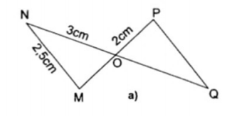
1. Cho hình vẽ bên, $\Delta $NOM = $\Delta $QOP và các cạnh có số đo ghi trên hình vẽ. Tính các cạnh còn lại của 2 tam giác. Chứng minh rằng MN // PQ.

2. Cho góc nhọn $\widehat{xOy}$, trên Ox và Oy lấy điểm A và B sao cho OA = OB. Vẽ hai đường tròn tâm A và tâm B có cùng độ dài bán kính (bán kính nhỏ hơn OA) chúng cắt nhai tại hai điểm E và F. Chứng minh rằng:

a) $\Delta $OEA = $\Delta $OEB; $\Delta $OFA = $\Delta $OFB

b) Ba điểm O, E, F thẳng hàng

c) FO là tia phân giác của góc $\widehat{AFB}$

3. Cho $\Delta $ABC. Lấy điểm B làm tâm vẽ đường tròn (B; AC). Lấy điểm C làm trâm vẽ đường tròn (C; AB). Hai đường tròn này cắt nhau tại hai điểm E và F thuộc hai nửa mặt phẳng đối nhau bờ là BC

a) Chứng minh các tam giác $\Delta $ABC = $\Delta $ECB = $\Delta $FCB

b) Chứng minh AB // CF, AC // BF

c) Chứng minh $\Delta $ABE = $\Delta $ECA

4. Cho $\Delta $ABC có AB = AC và H là trung điểm của cạnh BC. Chứng minh AH vuông góc với BC.

02 Bài giải:

1.

$\Delta $NOM = $\Delta $QOP $\Rightarrow $ OM = OP = 2cm ; OQ = ON 3cm; PQ = MN = 2,5cm

$\Delta $NOM = $\Delta $QOP $\Rightarrow $ $\widehat{MNO}=\widehat{PQO}$. Mà hai góc này ở vị trí so le trong nên MN // PQ

2.

Do độ dài bán kính bằng $\frac{1}{2}OA$ nên E và F nằm trong góc $\widehat{xOy}$.

a) Xét $\Delta $OEA và $\Delta $OEB có:

• OE chung
• OA = OB (giả thiết)
• AE = BE (E thuộc đường tròn tâm A và B có bán kính bằng nhau)

$\Rightarrow $ $\Delta $OEA = $\Delta $OEB (c.c.c)

Xét $\Delta $OFA và $\Delta $OFBcó:

• OF chung
• OA = OB (giả thiết)
• AF = BF (F thuộc đường tròn tâm A và B có bán kính bằng nhau)

$\Rightarrow $ $\Delta $OFA = $\Delta $OFBcó: (c.c.c)

b)

$\Delta $OEA = $\Delta $OEB $\Rightarrow \widehat{EOA}=\widehat{EOB}$ (hai góc tương ứng)

Do đó OE là tia phân giác của góc $\widehat{AOB}$ (1)

$\Delta $OFA = $\Delta $OFB $\Rightarrow \widehat{AOF}=\widehat{BOF}$ (hai góc tương ứng)

Do đó OF là tia phân giác của góc $\widehat{AOB}$ (2)

Từ (1) và (2) suy ra OE và OF trùng nhau, hay O, E, F thẳng hàng

c)

$\Delta $OFA = $\Delta $OFB $\Rightarrow \widehat{AFO}=\widehat{BFO}$ (hai góc tương ứng)

Do đó OF là tia phân giác của góc $\widehat{AFB}$

3.

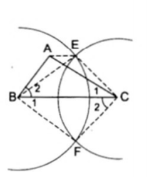
a) Xét $\Delta $ABC và $\Delta $ECB có:

• BC chung
• AC = BE (E thuộc đường tròn (B; AC))
• AB = CE (E thuộc đường tròn (C; AB))

Vậy $\Delta $ABC = $\Delta $ECB (c.c.c) (1)

Xét $\Delta $ECB và $\Delta $FCB có:

• BC chung
• CE = CF
• BF = BF (cùng bán kính)

Vậy $\Delta $ECB = $\Delta $FCB (c.c.c) (2)

Từ (1) và (2) suy ra $\Delta $ABC = $\Delta $ECB = $\Delta $FCB

b) Ta có: $\Delta $ABC = $\Delta $FCB $\Rightarrow \widehat{C_{1}}=\widehat{B_{1}}$ và $\widehat{C_{2}}=\widehat{B_{2}}$

Có: $\widehat{C_{1}}=\widehat{B_{1}}$ mà hai góc này ở vị trí so le trong của hai đường thẳng AC, BF cắt bởi BC nên AC // BF

$\widehat{C_{2}}=\widehat{B_{2}}$ mà hai góc này ở vị trí so le trong của hai đường thẳng AB, CF cắt bởi BC nên AC // BF

c) Xét $\Delta $ABE và $\Delta $ECA có:

• chung AE
• AB = EC
• BE = AC

$\Rightarrow $ $\Delta $ABE = $\Delta $ECA

4.

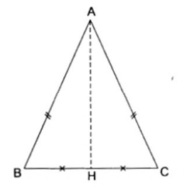
Xét $\Delta $ABH và $\Delta $ACH có:

• AH chung
• AB = AC (giả thiết)
• BH = HC (H là trung điểm của BC)

$\Rightarrow $ $\Delta $ABH = $\Delta $ACH (c.c.c)

$\Rightarrow \widehat{AHB}=\widehat{AHC}$ (hai góc tương ứng)

Mà $\widehat{AHB}=\widehat{AHC}=180^{\circ}$

$\Rightarrow \widehat{AHB}=\widehat{AHC}=90^{\circ}$

Do đó AH $\perp $ BC