Bảng Công Thức Logarit, Lũy Thừa, Mũ Dễ Nhớ - Tin Công Chức

Chuyển đến nội dung

HomeGiáo viên- Học SinhBài giảng toánToán 12Giải tích 12Bảng công thức logarit, lũy thừa, mũ dễ nhớ

Xem nhiều tuần qua:

• Bảng nguyên hàm lượng giác đầy đủ - cơ bản và mở rộng
• Tổng hợp các câu tìm nguyên hàm trong đề thi THPTQG các năm
• Tính nhanh nguyên hàm từng phần bằng sơ đồ
• Các dạng toán tìm cực trị của hàm số thi THPTQG
• Tìm nguyên hàm bằng máy tính Casio nhanh và chính xác

Bảng công thức logarit, lũy thừa, mũ dễ nhớ. Hàm số mũ và logarit là một trong những chuyên đề quan trọng trong chương trình môn Toán lớp 12. Tuy nhiên để giải tốt các bài toán liên quan đến logarit, học sinh cần thuộc tất cả các công thức. Dưới đây là tổng hợp các công thức quan trọng được sử dụng trong chương trình phổ thông.

1. Định nghĩa Logarit

Logarit viết tắt là Log là phép toán nghịch đảo của lũy thừa. Theo đó, logarit của một số a là số mũ của cơ số b (giá trị cố định), phải được nâng lên lũy thừa để tạo ra số a đó. Một cách đơn giản, logarit là một phép nhân có số lần lặp đi lặp lại.

2. Công thức Logarit

a. Các công thức Logarit đầy đủ

Bảng công thức: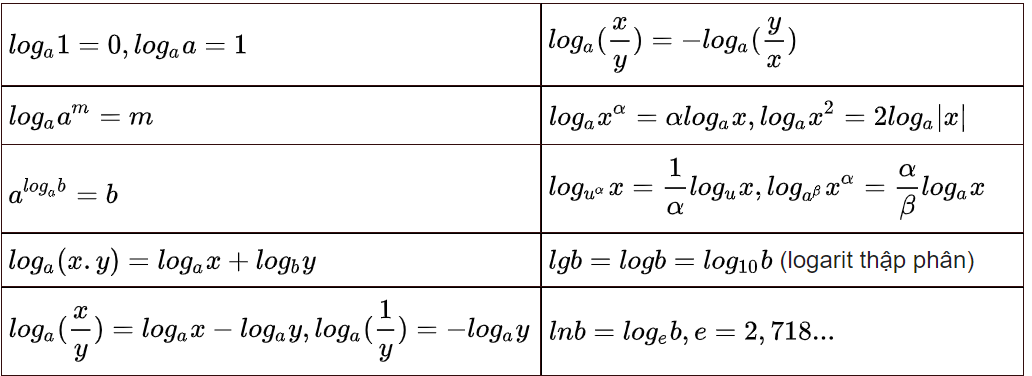

b. Công thức đạo hàm Logarit

c. Công thức Logarit Nepe

d. Công thức đổi cơ số

e. Công thức lũy thừa, mũ

Để ghi nhớ các công thức một cách nhanh chóng, chính xác và lâu dài học sinh cần làm nhiều bài tập dạng biến đổi. Thông qua việc làm bài tập các em sẽ thuộc công thức nhanh hơn. Like share và ủng hộ chúng mình nhé: Tags: bài tập logaritcông thức logarit cơ số 10công thức logarit cơ số ecông thức logarit đạo hàmcông thức logarit lncông thức logarit nepecông thức mũ logarit

Bài viết khác cùng mục:

Tính nhanh nguyên hàm từng phần bằng sơ đồ Các dạng bài tập tìm GTLN và GTNN của hàm số lượng giác 160 câu trắc nghiệm hàm số lớp 12 có đáp án Cách giải bất phương trình Mũ Logarit chứa tham số dùng bảng biến thiên Tổng hợp các câu hỏi về Mũ và Logarit trong đề thi THPTQG từ 2017 đến nay Phương pháp hàm số giải phương trình Mũ Logarit thi THPTQG Tìm m để phương trình mũ có nghiệm thỏa mãn – Phương trình mũ chứa tham số Cách bấm máy tính Logarit nhanh và chính xác nhất Cách biến đổi đẳng thức cho trước thành đẳng thức Logarit dễ hiểu – Biến đổi biểu thức Logarit Cho đồ thị của hàm y’, cách xác định GTLN GTNN của hàm hợp Tìm m để hàm số có GTLN GTNN thỏa mãn điều kiện cho trước Giải tích 12 – Cực trị hàm hợp, sự biến thiên của hàm hợp Bài viết mới

• TÔNG HỢP REVIEW Vòng Phỏng vấn Vietcombank đợt 1 NĂM 2025
• Tài liệu ôn thi Agribank 2025
• Bộ Văn hóa, Thể thao và Du lịch tuyển dụng viên chức năm 2025
• Bài tập hằng đẳng thức lớp 8 (download pdf)
• Tài liệu ôn thi công chức môn kiến thức chung

• Chia sẻ
• Sức khỏe
  • Dạy trẻ
• Giáo án
  • GA môn Công Nghệ
  • Giáo án toán 10
  • Lớp 7 Chân Trời Sáng tạo
    • GA Môn Toán 7
    • GA môn Văn 7
  • Lớp 7 sách Cánh Diều
    • GA Môn Toán 7
  • Lớp 7 sách Kết nối tri thức
    • GA môn Toán 7
    • GA môn Văn
  • Tài liệu cho giáo viên
• Giáo viên- Học Sinh
  • Bài giảng toán
    • Toán 6
      • Thi vào lớp 6 chuyên
      • Toán 6 Chân trời sáng tạo
      • Toán 6 KNTT
    • Toán 7
    • Toán 8
    • Toán 9
    • Toán 10
    • Toán 11
    • Toán 12
      • Giải tích 12
      • Hình học 12
  • Văn học
    • Ngữ Văn 9
    • Ngữ văn 10
    • Ngữ Văn 11
    • Ngữ văn 12
  • Tuyển sinh vào 10
    • Thi vào lớp 10 chuyên
  • Tiểu học
• Tài liệu chung
  • English
  • Tài liệu cao học
  • Tài liệu khác
  • Trắc nghiệm tin học
• Tuyển công chức
  • Tài liệu+ tin tuyển chung
    • Công chức thuế
    • Hải quan
    • Kho bạc nhà nước
    • Giáo dục
    • Ngân hàng
    • Tòa án-Viện kiểm sát
  • Tin tuyển dụng công chức
    • Tin tuyển sinh