Bảng đạo Hàm Cơ Bản Và Nâng Cao đầy đủ Nhất

Trang chủ » Với F(x)=2x+3 Và G(x)=sin X Thì Hàm F(g(x)) Là Hàm Nào Trong Các Hàm Dưới đây » Bảng đạo Hàm Cơ Bản Và Nâng Cao đầy đủ Nhất

Có thể bạn quan tâm

Bảng đạo hàm cơ bản và nâng cao đầy đủ nhất Nhựt Hoàng - Từ điển toán học Nhựt Hoàng Đăng: 25/10/2019 156693 lượt xem Bảng công thức đạo hàm

Bảng công thức đạo hàm

Bảng đạo hàm, công thức đạo hàm từ cơ bản đến nâng cao: các công thức tính đạo hàm, công thức đạo hàm lượng giác, công thức đạo hàm hàm số đa thức…

Bảng đạo hàm của hàm số biến x

Dưới đây là bảng đạo hàm các hàm số đa thức, hàm số lượng giác, hàm số mũ và hàm số logarit cơ bản biến x.

Bảng đạo hàm các hàm số cơ bản
(xα)’ = α.xα-1
(sin x)’ = cos x
(cos x)’ = – sin x

(tan x)’ = \[ \frac{1}{cos^2 x}\] = 1 + tan2 x

(cot x)’ = \[ \frac{-1}{sin^2 x}\] = -(1 + cot2 x)

(logα x)’ = \[ \frac{1}{x.lnα}\]

(ln x)’ = \[ \frac{1}{x}\]

(αx)’ = αx . lnα

(ex)’ = ex

Xem thêm: Công thức diện tích hình tròn

Bảng đạo hàm của hàm số biến u = f(x)

Dưới đây là bảng đạo hàm các hàm số đa thức, hàm số lượng giác, hàm số mũ và hàm số logarit của một hàm số đa thức u = f(x).

Bảng đạo hàm các hàm số nâng cao
(uα)’ = α.u’.uα-1
(sin u)’ = u’.cos u
(cos u)’ = – u’.sin u
(tan u)’ = \[ \frac{u’}{cos^2 u}\] = u'(1 + tan2 u)
(cot u)’ = \[ \frac{-u}{sin^2 u}\] = -u'(1 + cot2 x)
(logα u)’ = \[ \frac{u}{u.lnα}\]
(ln u)’ = \[ \frac{u’}{u}\]
(αu)’ = u’.αu.lnα
(eu)’ = u’.eu

Các công thức đạo hàm cơ bản

1. Đạo hàm của một số hàm số thường gặp

Định lý 1: Hàm số \[ y = {x^n}(n \in \mathbb{N}, n > 1) \] có đạo hàm với mọi \[x \in\mathbb{R} \] và: \[{\left( {{x^n}} \right)’} = n{x^{n – 1}}\].

Nhận xét:

(C)’= 0 (với C là hằng số).

(x)’=1.

Định lý 2: Hàm số \[y= \sqrt {x} \] có đạo hàm với mọi x dương và: \[\left( {\sqrt x } \right)’ = \frac{1}{{2\sqrt x }}\].

2. Đạo hàm của phép toán tổng, hiệu, tích, thương các hàm số

Định lý 3: Giả sử \[u = u\left( x \right) và v = v\left( x \right)\] là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:

\[{\left( {u + v} \right)’} = {u’} + {v’}\];

\[{\left( {u – v} \right)’} = {u’} – {v’}\];

\[{\left( {u.v} \right)’} = {u’}.v + u.{v’}\];

\[\left ( \frac{u}{v} \right )’=\frac{u’v-uv’}{v^2},(v(x) \ne 0)\]

Mở rộng:

\[({u_1} + {u_2} + … + {u_n})’ = {u_1}’ + {u_2}’ + … + {u_n}’\].

Hệ quả 1: Nếu k là một hằng số thì: (ku)’ = ku’.

Hệ quả 2: \[ {\left( {\frac{1}{v}} \right)’} = \frac{{ – v’}}{{{v^2}}} , (v(x)\ne 0)\]

\[(u.v.{\rm{w}})’ = u’.v.{\rm{w}} + u.v’.{\rm{w}} + u.v.{\rm{w}}’\]

3. Đạo hàm của hàm hợp

Định lý: Cho hàm số y = f(u) với u = u(x) thì ta có: \[y’_u=y’_u.u’_x\].

Hệ quả:

\[({u^n}) = n.{u^{n – 1}}.u’,n \in \mathbb{N}^*\].

\[\left( {\sqrt u } \right)’ = \frac{{u’}}{{2\sqrt u }}\].

Công thức đạo hàm lượng giác

Ngoài những công thức đạo hàm lượng giác nêu trên, ta có một số công thức bổ sung dưới đây:

[arcsin(x)]’ = \[ \frac{1}{ \sqrt{1 – x^2}}\]

[arccos(x)]’ = \[ \frac{-1}{ \sqrt{1 – x^2}}\]

[arctan(x)]’ = \[ \frac{1}{x^2 + 1}\]

Công thức đạo hàm cấp 2

Hàm số y = f(x) có đạo hàm tại x ∈ (a; b).

Khi đó y’ = f'(x) xác định một hàm sô trên (a;b).

Nếu hàm số y’ = f'(x) có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x.

Kí hiệu: y” hoặc f”(x).

Ý nghĩa cơ học: 

Đạo hàm cấp hai f”(t) là gia tốc tức thời của chuyển động S = f(t) tại thời điểm t.

Công thức đạo hàm cấp cao

Cho hàm số y = f(x) có đạo hàm cấp n-1 kí hiệu f (n-1) (x) (n ∈ N, n ≥ 4).

Nếu f (n-1) (x) có đạo hàm thì đạo hàm của nó được gọi là đạo hàm câp n của y = f(x), y (n) hoặc f (n) (x).

f (n) (x) = [f (n-1) (x)]’

Công thức đạo hàm cấp cao:

(x m)(n) = m(m – 1)(m – 2)…(m – n + 1).xm – n  (nếu m ≥ n)

(x m)(n) = 0 (nếu m ≤ n)

Xem tiếp các công thức đạo hàm còn lại một cách đầy đủ nhất ở bảng đạo hàm bên dưới:

Bảng đạo hàm tổng hợp đầy đủ nhất

Xem thêm bảng công thức đạo hàm cơ bản và nâng cao

Bảng công thức đạo hàm cơ bản và nâng cao

Bảng công thức đạo hàm cơ bản và nâng cao

Như vậy là các bạn đã được bổ sung lại kiến thức cơ bản và nâng cao về đạo hàm của hàm số thông qua bảng công thức đạo hàm trên đây. Các bạn có thể xem các bài tập về đạo hàm trên website TuDienToanHoc.Com.

5 / 5 ( 13 bình chọn ) Nhựt Hoàng - Từ điển toán học Nhựt Hoàng

Nhựt Hoàng sinh năm 1995 tại Nam Định trong một gia đình giáo viên nên được truyền thụ tình yêu với toán từ khi còn bé. Tự nhận thấy bản thân có một chút năng khiếu về toán nên mình quyết định xem toán học là niềm đam mê và theo đuổi lâu dài. Mình lập website này mong muốn chia sẻ tới mọi người niềm đam mê, tình yêu toán học, một trong những môn khoa học vĩ đại nhất từ xưa tới nay.

Bài viết liên quan

  • Công thức đại số tổ hợp

    Nhựt Hoàng - Từ điển toán học Nhựt Hoàng 93109 lượt xem

    Công Thức Tổ Hợp, Chỉnh Hợp, Hoán Vị HOÁN VỊ Số hoán vị của n phần tử: Pn = n! Các Nguyên Tắc Về Phép Đếm PHÉP ĐẾM 1. NGUYÊN TẮC ĐẾM Có 2 biến cố

  • Cách tính Thể Tích Khối Cầu (Hình Cầu)

    Cách tính Thể Tích Khối Cầu Nhựt Hoàng - Từ điển toán học Nhựt Hoàng 94097 lượt xem

    Khối cầu là một hình dạng vật thể phổ biến trong đời sống: quả bóng chuyền, quả cầu pha lê, Trái Đất… Do đó, bạn cần phải biết cách tính Thể

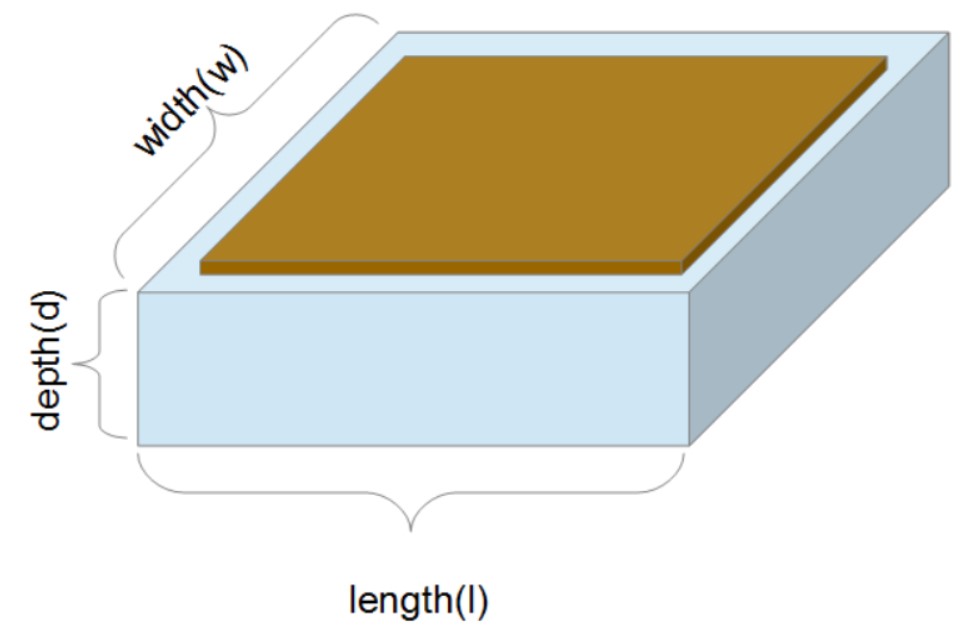
  • Công Thức Tính Thể Tích Hình Hộp Chữ Nhật

    Công Thức Tính Thể Tích Hình Hộp Chữ Nhật Nhựt Hoàng - Từ điển toán học Nhựt Hoàng 21378 lượt xem

    Thể tích hình hộp chữ nhật được xác định dễ dàng khi bạn biết chiều dài, chiều rộng và chiều cao của hình hộp. Các bạn đã biết đến công thức tính

  • Cách tính Thể Tích Hình Trụ

    Cách tính Thể Tích Hình Trụ Nhựt Hoàng - Từ điển toán học Nhựt Hoàng 98680 lượt xem

    Hình trụ là gì? Cách tính thể tích hình trụ như thế nào? Những bài tập áp dụng công thức tính thể tích hình trụ sẽ được trình bày trong bài viết sau

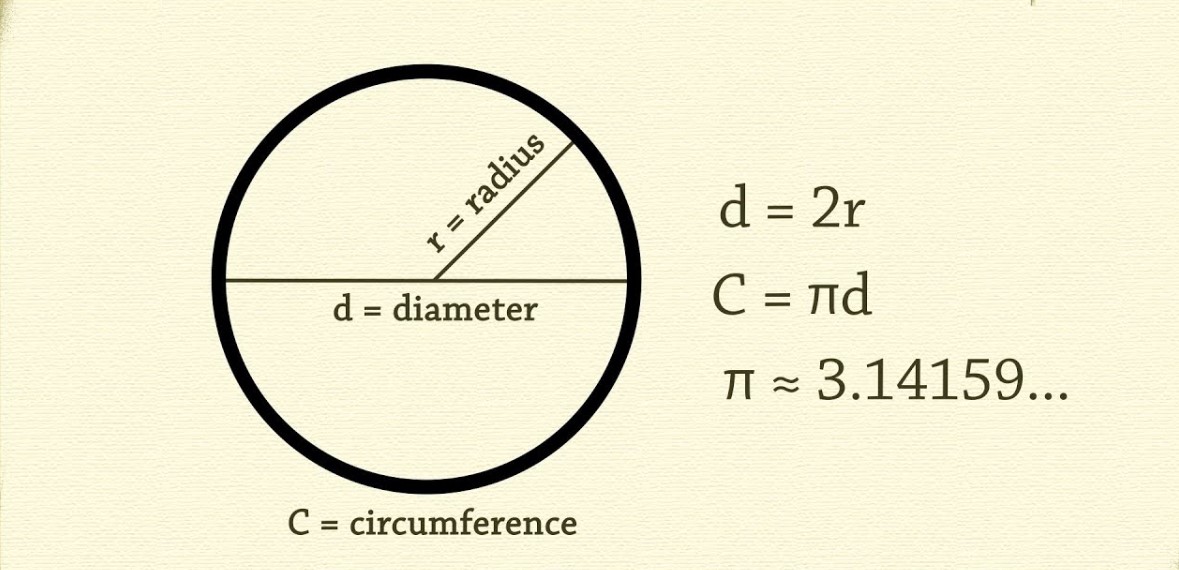
  • Công thức tính chu vi hình tròn và bài tập ví dụ

    Công thức tính chu vi hình tròn Nhựt Hoàng - Từ điển toán học Nhựt Hoàng 123312 lượt xem

    Chu vi hình tròn là gì? Công thức tính chu vi hình tròn, bài tập về cách tính chu vi hình tròn. Chu vi hình tròn Chu vi hình tròn là độ dài đường tròn hay còn gọi

  • Diện tích hình tròn là gì? Công Thức tính và Bài Tập ví dụ liên quan

    Công thức tính diện tích hình tròn Nhựt Hoàng - Từ điển toán học Nhựt Hoàng 194948 lượt xem

    Diện tích hình tròn là gì? (Diện tích thương được viết tắt là S hoặc DT). Bài viết sau đây sẽ gửi tới các bạn 3 phần là định nghĩa, công thức tính và

Chuyên mục

  • Sách, Tài liệu
  • Khảo sát hàm số
  • Chuyên đề
  • Wiki Toán Học
  • Toán lớp 4
  • Toán lớp 2
  • Toán lớp 1
  • Toán lớp 10
  • Toán lớp 9
  • Toán lớp 8
  • Toán lớp 3
  • Hỏi Đáp
  • Công Thức
  • Toán lớp 6
  • Từ điển toán

Phổ biến

  • Từ điển toán học

    Giải toán lớp 6 bài 1: Tập hợp. Phần tử của tập hợp

    09/09/2019 198220 lượt xem
  • Diện tích hình tròn là gì? Công Thức tính và Bài Tập ví dụ liên quan

    Diện tích hình tròn là gì? Công Thức tính và Bài Tập ví dụ liên quan

    25/10/2019 194948 lượt xem
  • Đề thi học kì 2 lớp 3 môn Toán – Đề 3

    Đề thi học kì 2 lớp 3 môn Toán – Đề 3

    14/06/2020 187592 lượt xem
  • Từ điển toán học

    Giải bài tập luyện tập trang 98 99 100 SGK toán lớp 6 tập 1

    09/11/2019 176335 lượt xem
  • Bất đẳng thức Cosi – Công thức, bài tập cơ bản và nâng cao

    Bất đẳng thức Cosi – Công thức, bài tập cơ bản và nâng cao

    10/09/2019 176210 lượt xem
  • Bán Trú Vệ Tinh Tại Tân Bình UY TÍN

    Bán Trú Vệ Tinh Tại Tân Bình UY TÍN

    26/05/2020 176107 lượt xem
  • Từ điển toán học

    Giải toán lớp 6 bài 7 chương 2: Phép trừ hai số nguyên

    24/10/2019 175286 lượt xem
  • Từ điển toán học

    Giải bài tập Luyện tập 2 trang 19 – 20 SGK toán lớp 6 tập 1

    16/09/2019 175174 lượt xem
  • Từ điển toán học

    Giải toán lớp 6 bài 2 hình học: Ba Điểm Thẳng Hàng

    11/11/2019 174912 lượt xem
  • Từ điển toán học

    Giải bài tập luyện tập 1 trang 59, 60 SGK toán lớp 6 tập 1

    08/10/2019 174332 lượt xem

Thuật ngữ tìm nhiều

  • bicircular quartic là gì? (152256 lượt xem)
  • synthetical substituend là gì? (152177 lượt xem)
  • neutral equilibrium là gì? (152171 lượt xem)
  • universal joint là gì? (152022 lượt xem)
  • mutiplicatively closed là gì? (151847 lượt xem)

Đề xuất

  • Sách các chuyên đề hình học bồi dưỡng học sinh giỏi THCS

    Sách các chuyên đề hình học bồi dưỡng học sinh giỏi THCS

    12/03/2022 3844 lượt xem
  • Từ điển toán học

    Giải toán lớp 6 bài 2 chương 2: Tập hợp các số nguyên

    19/10/2019 89706 lượt xem
  • Diện tích hình tròn là gì? Công Thức tính và Bài Tập ví dụ liên quan

    Diện tích hình tròn là gì? Công Thức tính và Bài Tập ví dụ liên quan

    25/10/2019 194948 lượt xem

Page Từ Điển Toán Học

    Từ Điển Toán Học
arrow_upward
    TỪ ĐIỂN TOÁN HỌC.COM
  • Giới thiệu
  • Liên hệ

    • Copyright© 2019 Tudientoanhoc.com

Yêu cầu bổ sung thuật ngữ toán học cần dịch

Gửi yêu cầu

Mỗi một yêu cầu bổ sung thuật ngữ toán học của bạn là một đóng góp to lớn cho sự hoàn thiện của chúng tôi. Xin chân thành cảm ơn!

Hủy

Gửi câu hỏi toán học và nhận giải đáp miễn phí từ Nhựt Hoàng cùng các cộng sự

Gửi câu hỏi Hủy

Đăng ký nhận thông báo khi có bài viết mới

Gửi yêu cầu Hủy apps
  • notifications_active
  • format_quote
  • mode_edit

Từ khóa » Với F(x)=2x+3 Và G(x)=sin X Thì Hàm F(g(x)) Là Hàm Nào Trong Các Hàm Dưới đây