Bất đẳng Thức Lớp 10 Và Cách Giải Bài Tập

Bất đẳng thức lớp 10 và cách giải bài tập – Toán lớp 10

I. Lý thuyết về Bất đẳng thức

1. Bất đẳng thức là gì?

Các mệnh đề dạng “a > b” hoặc “a < b” được gọi là bất đẳng thức.

Nếu mệnh đề “a < b⇒ c < d” đúng thì ta nói bất đẳng thức c < d là bất đẳng thức hệ quả của bất đẳng thức a < b và cũng viết là a < b⇒ c < d.

Nếu bất đẳng thức a < b là hệ quả của bất đẳng thức c < d và ngược lại thì ta nói hai bất đẳng thức tương đương với nhau và viết là a < b ⇔c < d.

2. Tính chất của bất đẳng thức

Tên gọi và điều kiện		Nội dung
Cộng hai vế của bất đẳng thức với số bất kì		a<b⇔a+c<b+c
Nhân hai vế của bất đẳng thức với một số	c > 0	a<b⇔ac<bc
	c < 0	a<b⇔ac>bc
Cộng hai bất đẳng thức cùng chiều		a>bc>d⇒a+c>b+d
Nhân hai bất đẳng thức cùng chiều		0<a<b0<c<d⇒ac<bd
Nâng hai vế của bất đẳng thức lên một lũy thừa	n∈ℕ*	a<b⇔a2n+1<b2n+1
	n∈ℕ*và a > 0	a<b⇔a2n<b2n
Khai căn hai vế của một bất đẳng thức	a > 0	a<b⇔a<b
	a bất kỳ	a<b⇔a3<b3

Chú ý

Ta còn gặp các mệnh đề dạng a ≤ b hoặc a ≥ b. Các mệnh đề dạng này cũng được gọi là bất đẳng thức. Để phân biệt, ta gọi chúng là các bất đẳng thức không ngặt và gọi các bất đẳng thức dạng a < b hoặc a > b là các bất đẳng thức ngặt. Các tính chất nêu trong bảng trên cũng đúng cho bất đẳng thức không ngặt.

3. Bất đẳng thức hệ quả và bất đẳng thức tương đương

- Nếu mệnh đề "a < b => c < d" đúng thì ta nói bất đẳng thức c < d là bất đẳng thức hệ quả của bất đẳng thức a<b và cũng viết là a < b => c < d

Ví dụ: a < b và b < c => a < c (tính chất bắc cầu)

a < b, c tùy ý => a + c < b + c (tính chất cộng hai vế bất đẳng thức với một số)

- Nếu bất đẳng thức a < b là hệ quả của bất đẳng thức c < d và ngược lại thì ta nói hai bất đẳng thức tương đương với nhau và viết là a < b ⇔ c < d

II. Các bất đẳng thức thường gặp

1. Bất đẳng thức Cô-si

∀a≥0; b≥0 thì ta có: a+b2≥ab. Dấu “=” xảy ra khi và chỉ khi a=2

Hệ quả 1: Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.

a+1a≥2,     ∀a>0.

Hệ quả 2: Nếu hai số dương có tổng không đổi thì tích của chúng lớn nhất khi hai số bằng nhau.

Hệ quả 3: Nếu hai số dương có tích không đổi thì tổng của chúng nhỏ nhất khi hai số bằng nhau.

2. Bất đẳng thức chứa dấu giá trị tuyệt đối

Ta có các tính chất cho trong bảng sau:

Điều kiện	Nội dung
|x| ≥0, |x| ≥x, |x| ≥−x
a > 0	|x| ≤a⇔−a≤x≤a
	|x| ≥a⇔x≤−ax≥a
|a| −|b| ≤ |a+b| ≤ |a|+|b|

3. Bất đẳng thức Bunhiacopxki

+ Bất đẳng thức Bunhiacopxki dạng cơ bản:

Dấu “=” xảy ra khi và chỉ khi

+ Bất đẳng thức Bunhiacopxki cho 2 bộ số:

Với hai bộ sốvàta có:

Dấu “=” xảy ra khi và chỉ khi

Với quy ước nếu một số nào đó (i = 1, 2, 3, …, n) bằng 0 thì tương ứng bằng 0

III. Các dạng bài tập bất đẳng thức

Dạng 1: Chứng minh bất đẳng thức nhờ định nghĩa

a. Phương pháp giải:

Để chứng minh A≥B (hoặc A > B), ta làm các bước sau:

Bước 1: xét hiệu A – B.

Bước 2: chứng minh A−B≥0 ( hoặc A – B > 0).

Sử dụng linh hoạt kiến thức ở phần lý thuyết để chứng minh ở bước 2.

Bước 3: kết luận.

Bước 4: xét A = B khi nào?

b. Ví dụ minh họa:

Ví dụ 1: Cho a, b > 0. Chứng minh rằng:ab+ba≥2 .

Hướng dẫn:

Ta có:

ab+ba−2=a2+b2−2abab=(a−b)2ab≥0

(do a, b > 0)

Vậy ab+ba≥2.

Dấu “=” xảy ra khi và chỉ khi a = b.

Ví dụ 2: Cho a, b, c là 3 số tuỳ ý, chứng minh rằng: a2+b2+c2 ≥ ab+bc+ca.

Hướng dẫn:

Xét biểu thức: M=a2+b2+c2–ab+bc+ca.

Suy ra:

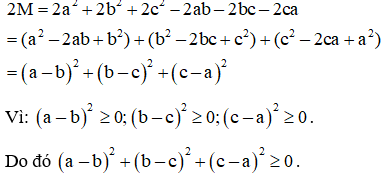
Suy ra 2a2+2b2+2c2−2ab–2bc–2ca≥0

hay a2+b2+c2–ab+bc+ca≥0

Vậy a2+b2+c2 ≥ ab+bc+ca.

Dấu “=” xảy ra khi và chỉ khi a = b = c.

Dạng 2: Sử dụng bất đẳng thức Cô-si

a. Phương pháp giải:

Một số chú ý khi sử dụng bất đẳng thức Cô-si:

- Khi áp dụng bất đẳng thức Cô-si thì các số phải là những số không âm

- Bất đẳng thức Cô-si thường được áp dụng khi trong bất đẳng thức cần chứng minh có tổng và tích

- Điều kiện xảy ra dấu “=” là các số bằng nhau

- Bất đẳng thức Cô-si còn có hình thức khác thường hay sử dụng:

Đối với hai số: x2+y2≥2xy; x+y≥2xy với mọi x;y≥0

Đối với ba số:abc≤a3+b3+c33 ; a+b+c≥3abc3 với mọi a;b;c≥0

b. Ví dụ minh họa:

Ví dụ 1: Cho ba số thực dương x, y, z. Chứng minh rằng:

xyz+yzx+zxy≥1x+1y+1z.

Hướng dẫn:

Vì x, y, z là các số thực dương suy ra xyz,yzx,zxy là các số dương. Áp dụng bất đẳng thức Cô-si, ta có:

xyz+yxz≥2.xyz.yxz=2z (1)

xyz+zxy≥2.xyz.zxy=2y (2)

zxy+yzx≥2.zxy.yzx=2x (3)

Cộng các vế của (1), (2) và (3) ta được

2xyz+yzx+zxy≥21x+1y+1z

Hay xyz+yzx+zxy≥1x+1y+1z

Dấu “=” xảy ra khi và chỉ khi x = y = z.

Ví dụ 2: Cho ba số thực dương a, b, c thỏa mãn a + b + c = 1. Chứng minh rằng: 1a+4b+9c≥36?

Hướng dẫn:

Áp dụng bất đẳng thức Cô-si cho hai số thực dương ta có:

1a+36a≥21a.36a=12 (1)

4b+36b≥24b.36b=24 (2)

9c+36c≥29c.36c=36(3)

Cộng các vế tương ứng của (1), (2), (3) ta được

1a+4b+9c+36(a+b+c)≥72⇒1a+4b+9c≥36

(do a + b + c = 1)

Dấu “=” xảy ra khi và chỉ khi 1a=36a; 4b=36b; 9c=36c và a + b + c = 1 hay a=16; b=13; c=12.

Dạng 3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đại lượng nhờ bất đẳng thức

a. Phương pháp giải:

Vận dụng các tính chất của bất đẳng thức, bất đẳng thức Cô-si, bất đẳng thức chứa dấu giá trị tuyệt đối,… để tìm giá trị lớn nhất, giá trị nhỏ nhất.

b. Ví dụ minh họa:

Ví dụ 1: Tìm giá trị nhỏ nhất của biểu thức P=x2+16x,  x>0.

Hướng dẫn:

Ta có: P=x2+16x =x2+8x+8x. Áp dụng bất đẳng thức Cô-si cho 3 số, ta có:

x2+8x+8x≥3x2.8x.8x3=12

Vậy giá trị nhỏ nhất của P là 12.

Dấu “=” xảy ra khi và chỉ khi x2=8x=8x⇔x=2.

Ví dụ 2: Trong các hình chữ nhật có chu vi bằng 300 m, hình chữ nhật có diện tích lớn nhất bằng bao nhiêu?

Hướng dẫn:

Giả sử hình chữ nhật có chiều dài và chiều rộng lần lượt là a, b (0 < a, b < 150) (đơn vị: mét)

Từ giả thiết, ta có a + b = 300 : 2 = 150 (m)

Diện tích hình chữ nhật là S=a.b (m2).

Áp dụng bất đẳng thức Cô-si, ta có:

a.b≤a+b2⇔a.b≤75⇔ab≤5625⇔S≤5625

Vậy hình chữ nhật có diện tích lớn nhất là 5625 m2.

Dấu bằng xảy ra

a=ba+b=150⇔a=b=75.

IV. Bài tập về Bất đẳng thức

1. Tự luận

Câu 1: Cho a, b là hai số tùy ý. Chứng minh rằng : a2+b22≥a+b22.

Hướng dẫn:

Xét hiệu:

a2+b22−a+b22

= 2a2+b24−a2+2ab+b24

=142a2+2b2−a2−b2−2ab

= 14a−b2≥0

Vậy a2+b22≥a+b22. Dấu “=” xảy ra khi a = b.

Câu 2: Cho a, b, c, d là các số thực, chứng minh rằng:

a2+b2+c2+d2+e2≥ab+c+d+e.

Hướng dẫn:

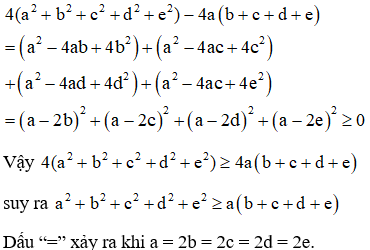
Câu 3: Chứng minh rằng:

b+cc+aa+b≥8abc ∀a,b,c≥0

Hướng dẫn:

Áp dụng bất đẳng thức Cô-si, ta có:

a+b≥2abb+c≥2bcc+a≥2ca⇒a+bb+cc+a≥8abc

Dấu “=” xảy ra ⇔a=b=c.

Câu 4: Chứng minh rằng: a2+8a2+4≥4

Hướng dẫn:

Ta có:

a2+8=(a2+4)+4≥2 (a2+4).4

( theo bất đẳng thức Cô-si)

Do đó:

a2+8a2+4≥2a2+4.4a2+4=4

Dấu “=” xảy ra ⇔a2+4=4⇔a=0

Câu 5: Cho a, b, c > 0 và a + b + c = 1. Chứng minh rằng:

1a2+2bc+1b2+2ac+1c2+2ab≥9(1)

Hướng dẫn:

Đặt x = a2+2bc; y = b2+2ac; z =c2+2ab ( do a, b, c > 0 nên x, y, z > 0)

Ta có:

x+y+z=a+b+c2=1

Với x + y + z = 1 và x, y, z > 0, theo bất đẳng thức Cô-si cho 3 số ta có:

x+y+z≥3xyz3.

và 1x+1y+1z≥31xyz3.

⇒x+y+z.1x+1y+1z≥9

Suy ra 1x+1y+1z≥9

hay 1a2+2bc+1b2+2ac+1c2+2ab≥9.

Câu 6: Tìm giá trị nhỏ nhất của hàm số y=4x4−3x2+9x2; x≠0.

Hướng dẫn:

Xét hàm số

y=4x4−3x2+9x2=4x2+9x2−3

Áp dụng bất đẳng thức Cô-si, ta có: 4x2+9x2≥24x2.9x2=12

⇒y≥9

Vậy giá trị nhỏ nhất của hàm số y=4x4−3x2+9x2 là 9 khi 4x2=9x2

⇔x2=32⇔x=±62

Câu 7: Cho x≥2. Tìm giá trị lớn nhất của hàm số fx=x−2x.

Hướng dẫn:

Ta có fx≥0 và fx2=x−2x2=1x−2x2

=18−21x−142≤18⇒0≤fx≤122=24.

Vậy giá trị lớn nhất của hàm số bằng 24 đạt được khi x=4

Câu 8: Tìm giá trị lớn nhất và giá trị nhỏ nhất m của hàm số y=6−2x+3+2x.

Hướng dẫn:

Tập xác định của hàm số D=−32;3.

Ta thấy y>0 ∀x∈−32;3.

Có:

y2=9+26−2x3+2x≥9 ∀x∈−32;3.

Suy ra y≥3;∀x∈−32;3.

Dấu bằng xảy ra khi x=−32x=3.

Vậy Min  yx∈−32;3=3.

Theo bất đẳng thức Cô-si ta có:

26−2x3+2x≤6−2x+3+2x=9

với  ∀x∈−32;3.

Suy ra:

y2≤18,∀x∈−32;3⇒y≤32,∀x∈−32;3

Dấu bằng xảy ra khi :

6−2x=3+2x⇔x=34

Vậy Max yx∈−32;3=32.

Câu 9: Cho các số thực a, b thỏa mãn ab>0. Tìm giá trị nhỏ nhất của biểu thức P=a2b2+b2a2−2ab−2ba−1.

Hướng dẫn:

Ta có:

P=a2b2+b2a2−2ab−2ba−1=a2b2−2ab+1+b2a2−2ba+1−3=ab−12+ba−12−3≥−3

Đẳng thức xảy ra khi và chỉ khi:

ab=1ba=1⇔a=b≠0.

Vậy giá trị nhỏ nhất của P là -3 khi a=b (a,b≠0).

Câu 10: Người ta dùng 100 m rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Biết một cạnh của hình chữ nhật là bức tường (không phải rào). Tính diện tích lớn nhất của mảnh vườn để có thể rào được?

Hướng dẫn:

Đặt cạnh của hình chữ nhật lần lượt là x, y (x, y > 0; y là cạnh của bức tường).

Ta có: 2x+y=100.

Diện tích hình chữ nhật là :

S=xy=2.x.y2≤C​osi2.x+y222=182x+y2=181002=1250

Vậy diện tích lớn nhất của mảnh vườn là 1250 m2 khi:

x=y2⇔y=2x⇒x=25 m; y=50 m.

2. Trắc nghiệm

Câu 1: Cho các bất đẳng thức a > b và c > d. Bất đẳng thức nào sau đây đúng

A. a−c>b−d.

B. a+c>b+d.

C. ac>bd.

D. ac>bd.

Hướng dẫn:

Chọn B.

Theo tính chất bất đẳng thức,a>bc>d⇔a+c>b+d

Câu 2: Suy luận nào sau đây đúng?

A. a>b>0c>d>0⇒ac>bd.

B. a>bc>d⇒a−c>b−d.

C. a>bc>d⇒ac>bd.

D. a>bc>d⇒ac>bd.

Hướng dẫn

Chọn A.

a>b>0c>d>0⇒ac>bd đúng theo tính chất nhân hai bất đẳng thức dương cùng chiều.

Câu 3: Bất đẳng thức nào sau đây đúng với mọi số thực a?

A. 6a>3a.

B. 3a>6a.

C. 6−3a>3−6a.

D. 6+a>3+a.

Hướng dẫn

Chọn D.

Ta có 6+a>3+a

⇔6+a−3−a>0

⇔3>0 đúng với mọi số thực a.

Câu 4: Cho a, b là các số thực bất kì. Trong các mệnh đề sau, mệnh đề nào sai?

A. a>b⇔a−b>0.

B. a>b>0⇒1a<1b.

C. a>b⇔a3>b3.

D. a>b⇔a2>b2.

Hướng dẫn

Chọn D.

Các mệnh đề A, B, C đúng.

Mệnh đề D sai. Ta có phản ví dụ: −2>−5 nhưng −22=4<25=−52.

Câu 5: Cho a > b khẳng định nào sau đây là đúng?

A. 2a<2b.

B. a>b−c,∀c∈ℝ.

C. −a<−b.

D. ac>cb,∀c∈ℝ.

Hướng dẫn

Chọn C.

Đáp án A sai ví dụ 2>0⇒2.2>2.0

Đáp án B sai với a = 3, b = 2, c = -2.

Đáp án C đúng vì −a<−b⇔a>b.

Đáp án D sai khi c≤0.

Câu 6: Trong các mệnh đề sau, mệnh đề nào sai?

A. a+b≤a+b.

B. x<a⇔−a<x<a,a>0.

C. a>b⇔ac>bc,∀c∈ℝ.

D. a+b≥2ab, a≥0,b≥0.

Hướng dẫn

Chọn C.

Các đáp án A, B đều đúng theo tính chất của bất đẳng thức chứa dấu giá trị tuyệt đối.

Đáp án D đúng theo bất đẳng thức Cô-si cho 2 số không âm a và b.

Đáp án C sai khi c < 0 (vì khi nhân 2 vế của một bất đẳng thức với một số âm thì ta được bất đẳng thức mới đổi chiều bất đẳng thức đã cho).

Câu 7: Cho hai số thực a và b thỏa mãn a + b = 4. Khẳng định nào sau đây đúng?

A. Tích a.b có giá trị nhỏ nhất là 2.

B. Tích a.b không có giá trị lớn nhất.

C. Tích a.b có giá trị lớn nhất là 4.

D. Tích a.b có giá trị lớn nhất là 2.

Hướng dẫn

Chọn C.

Với mọi số thực a và b ta luôn có:

a.b≤a+b24⇔a.b≤4.

Dấu “=” xảy ra ⇔a=b=2.

Câu 8: Giá trị nhỏ nhất của hàm số fx=2x+3x với x > 0 là:

A. 43.

B. 26.

C. 6.

D. 23.

Hướng dẫn

Chọn B.

Theo bất đẳng thức Cô-si ta có 2x+3x≥26 suy ra giá trị nhỏ nhất của f(x) bằng 26.

Câu 9: Tìm giá trị nhỏ nhất của biểu thức A=x−2+4−x.

A. 2.

B. 2.

C. 2−2

D. 0.

Hướng dẫn

Chọn B.

A=x−2+4−xcó tập xác định D=2; 4.

Ta có: A2=2+2x−24−x≥2

⇒A≥2, dấu bằng xảy ra khi x = 2 hoặc x = 4.

Câu 10: Cho các mệnh đề sau

ab+ba≥2  I;ab+bc+ca≥3  II ;

1a+1b+1c≥9a+b+c  III

Với mọi giá trị của a, b, c dương ta có:

A. (I) đúng và (II), (III) sai.

B. (II) đúng và (I), (III) sai.

C. (III) đúng và (I), (II) sai.

D. (I), (II), (III) đúng.

Hướng dẫn

Chọn D.

Với mọi a, b, c dương ta luôn có:

ab+ba≥2ab.ba⇔ab+ba≥2, dấu bằng xảy ra khi a = b. Vậy (I) đúng.

ab+bc+ca≥3ab.bc.ca3

⇔ab+bc+ca≥3, dấu bằng xảy ra khi a = b = c. Vậy (II) đúng.

a+b+c.1a+1b+1c≥3abc3.31abc3=9,

⇒1a+1b+1c≥9a+b+cdấu bằng xảy ra khi a = b = c. Vậy (III) đúng.

Xem thêm các dạng bài tập Toán lớp 10 có đáp án và lời giải chi tiết khác:

Bất phương trình bậc nhất và cách giải bài tập

Bất phương trình bậc hai và cách giải bài tập

Hệ bất phương trình bậc nhất một ẩn và cách giải bài tập

Bảng phân bố tần số và tần suất và cách giải bài tập

Biểu đồ lớp 10 và cách giải bài tập