Bát Giác – Wikipedia Tiếng Việt
Có thể bạn quan tâm

Trong hình học, một hình bát giác hay octagon (tiếng Hy Lạp ὀκτάγωνον oktágōnon, "tám góc") là một đa giác có tám cạnh. Một bát giác đều được thể hiện bằng biểu tượng Schläfli {8}. Mỗi chiều 135 độ.
Hình bát giác đều được ứng dụng nhiều trong nghệ thuật và kiến trúc.
Tính chất của bát giác
[sửa | sửa mã nguồn]
Cho bát giác A1A2···A2, gọi Cj với j=1,2,...,8, là tâm của các hình vuông đều dựng ra ngoài hoặc vào trong cạch AjAj+1. Khi đó trung điểm C1C5, C2C6, C3C7, C4C8 là các đỉnh của một tứ giác có hai đường chéo vuông góc và bằng nhau. Đây là kết quả mở rộng của định lý Van Aubel.[1]
Một số công thức của bát giác đều
[sửa | sửa mã nguồn]Tổng của tất cả góc của một hình bát giác đều nội bộ là 1080° và có nguồn gốc từ công thức:
Góc nội thất của hình bát giác đều
| Kích thước của một hình bát giác đều | ||
|---|---|---|
| Chiều dài cạnh | ||
| Diện tích | ||
| bán kính trong | ||
| bán kính chu vi | ||
| Đường chéo lớn | ||
| Đường chéo trung | ||
| Đường chéo nhỏ | ||
| Góc trong | ||
Xem thêm
[sửa | sửa mã nguồn]- Bát giác hồi hương
- Bát quái
- Tháp Bằng An
- Định lý Van Aubel
Hình ảnh
[sửa | sửa mã nguồn]-
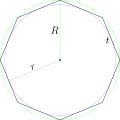 Một bát giác đều
Một bát giác đều -
 Một bát giác đều
Một bát giác đều -
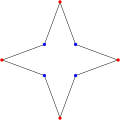 Bát giác lõm
Bát giác lõm -
 Bát giác lõm
Bát giác lõm -
 Một bát giác chéo phức tạp
Một bát giác chéo phức tạp -
 Sao bát giác
Sao bát giác -
 Thiết kế một hình bát giác
Thiết kế một hình bát giác -
 Vẽ hình bát giác bằng compa
Vẽ hình bát giác bằng compa -
-

-

-
-
 Đại hồi
Đại hồi -
 Một chiếc bàn bát giác
Một chiếc bàn bát giác -

-
Hình bát giác
-
 Gương bát quái
Gương bát quái -
Một chén hình bát giác
-
 Một bộ dĩa hoa lam thời Minh, thế kỷ 16
Một bộ dĩa hoa lam thời Minh, thế kỷ 16 -
 Hòm bát giác
Hòm bát giác -
 Lầu bát giác
Lầu bát giác -
 Tháp bát giác
Tháp bát giác -
Nhà bát giác (Octagon House) tại Watertown, WI.
-
McElroy Octagon House ở San Francisco
| |
|---|---|
|
Tham khảo
[sửa | sửa mã nguồn]- ^ "Dao Thanh Oai, Equilateral triangles and Kiepert perspectors in complex numbers,Forum Geometricorum, 15 (2015) 105--114" (PDF). Bản gốc (PDF) lưu trữ ngày 20 tháng 6 năm 2023. Truy cập ngày 20 tháng 6 năm 2015.
Bài viết liên quan đến hình học này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn. |
- x
- t
- s
Từ khóa » Tính Diện Tích Hình Bát Giác đều
-
Cách để Tính Diện Tích Của đa Giác đều - WikiHow
-
Hình Bát Giác đều? Cách Tính Diện Tích Hình Bát Giác đều, Góc Bằng ...
-
Diện Tích Hình Bát Giác
-
Cho Hình Bát Giác đều Có độ Dài Cạnh 3 Cm. Tính Diện Tích Bát Giác đó
-
Cách Tính Cạnh Hình Bát Giác đều - Quang An News
-
Cách Tính Cạnh Hình Bát Giác Đều, Cách Để Tính Diện Tích Của ...
-
Cách Tính Cạnh Hình Bát Giác đều - Xây Nhà
-
Công Thức Tính Diện Tích đa Giác đều N Cạnh - Mathvn
-
Diện Tích Và Chu Vi Của đa Giác đều - Phép Tính Online
-
Hình Bát Giác Là Gì? Xem Xong 5 Phút Hiểu Luôn. - Tintuctuyensinh
-
Đa Giác Đều - Công Thức, Cách Tính Diện Tích & Chu Vi
-
Bát Diện đều: Công Thức Tính Thể Tích Và Bài Tập - Toán Thầy Định
-
Tổng Diện Tích Các Mặt Khối Của Hình Bát Diện đều - Đáp Án Chuẩn
-
Cách Tính Cạnh Hình Bát Giác đều


































