Bất Phương Trình Bậc Nhất Một ẩn - Đại Số Toán 8
Có thể bạn quan tâm
Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Bất phương trình bậc nhất một ẩn lớp 8, tài liệu bao gồm 13 trang, tuyển chọn 9 ví dụ và 15 bài tập Bất phương trình bậc nhất một ẩn đầy đủ lý thuyết, phương pháp giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Tài liệu Bất phương trình bậc nhất một ẩn - Đại số toán 8 gồm các nội dung sau:
I. Phương pháp giải
- Tóm tắt lý thuyết ngắn gọn
II. Một số ví dụ
- Gồm 9 ví dụ minh họa đa dạng cho dạng bài Bất phương trình bậc nhất một ẩn có lời giải chi tiết
III. Bài tập vận dụng
- Gồm 15 bài tập vận dụng có lời giải chi tiết giúp học sinh rèn luyện cách giải các bài tập Bất phương trình bậc nhất một ẩn
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
I. Phương pháp giải
1. Bất phương trình ẩn x: có dạng A(x)>B(x) (hoặc A(x)<B(x);A(x)≥B(x);A(x)≤B(x)), trong đó Ax và Bx là hai biểu thức chứa biến x.
2. Bất phương trình bậc nhất một ẩn: có dạng ax+b>0 (hoặc ax+b<0;ax+b≥0;ax+b≤0) trong đó a và b là hai số đã cho, a≠0 .
3. Nghiệm của bất phương trình là giá trị của ẩn, khi thay vào bất phương trình được một khẳng định đúng. Tập hợp tất cả các nghiệm của một bất phương trình là tập nghiệm của nó. Giải một bất phương trình là tìm tập nghiệm của bất phương trình đó.
4. Hai bất phương trình tương đương: Có cùng tập nghiệm.
5. Quy tắc biến đổi bất phương trình:
a) Quy tắc chuyển vế: Khi chuyển vế một hạng tử của bất phương trình phải đổi dấu hạng tử đó.
b) Quy tắc nhân với một số: Khi nhân hai vế của bất phương trình với một số khác không ta phải: Giữ nguyên chiều bất phương trình nếu số đó dương, đổi chiều bất phương trình nếu số đó âm.
6. Bất phương trình dạng (hoặc đưa về dạng): ax+b>0(a≠0) có nghiệm x>-ba nếu a>0; x<-ba nếu a<0
Các bất phương trình ax+b<0;ax+b≥0;ax+b≤0(a≠0) giải tương tự.
II. Một số ví dụ
Ví dụ 1: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất một ẩn. Kiểm tra xem giá trị x=4 là nghiệm của bất phương trình nào trong các bất phương trình bậc nhất một ẩn.
a,2x+3y>6y+7 b, -5x+4<2-3x
c, -5y+8y+4<3-2,5y (y ần)
d, 8x-3≥1-6x+15x e, x2-6x+5≤0
Tìm cách giải: - Dựa vào định nghĩa, bất phương trình nào đưa được về dạng ax+b>0 (hoặc ax+b<0;ax+b≥0;ax+b≤0) trong đó a và b là hai số đã cho, a≠0. Có thể chỉ cần căn cứ bậc cao nhất của ẩn trong bất phương trình là bậc 1.
- Nghiệm của bất phương trình là giá trị của ẩn, khi thay vào bất phương trình được một khẳng định đúng. Do đó xét bất phương trình f(x)>g(x)(1) . Thay x=x0vào (1). Nếu f(x0)>g(x0) thì x=x0 là nghiệm của (1).
Nếu \[f\left( {{x_0}} \right) \le g\left( {{x_0}} \right)\] thì \[x = {x_0}\] không là nghiệm của (1).
(xét tương tự với các bất phương trình khác).
Giải
Các bất phương trình
b) \[ - 5x + 4 < 2 - 3x\] (ẩn x);
c) \[ - 5y + 8y + 4 < 3 - 2,5y\] (ẩn y);
d) \[8x - 3 \ge 1 - 6x + 15x\] (ẩn x);
là các bất phương trình bậc nhất một ẩn.
Do \[x = 4\] nên chỉ xét các bất phương trình ẩn x
Đặt \[f\left( x \right) = - 5x + 4;{\rm{ }}g\left( x \right) = 2 - 3x\]
\[h\left( x \right) = 8x - 3;{\rm{ }}p\left( x \right) = 1 - 6x + 15x\].
Ta có: * \[f\left( 4 \right) = - 5.4 + 4 = - 16;{\rm{ }}g\left( 4 \right) = 2 - 3.4 = - 10\].
\[f\left( 4 \right) < g\left( 4 \right)\] nên \[x = 4\] là nghiệm của bất phương trình \[ - 5x + 4 < 2 - 3x\].
* \[h\left( 4 \right) = 8.4 - 3 = 29;{\rm{ }}p\left( 4 \right) = 1 - 6.4 + 15.4 = 37\].
\[h\left( 4 \right) < p\left( 4 \right)\] nên \[x = 4\] không là nghiệm của bất phương trình \[8x - 3 \ge 1 - 6x + 15x\].
Ví dụ 2: Giải các bất phương trình bậc nhất một ẩn ở ví dụ 1 trên và biểu diễn nghiệm trên trục số.
* Tìm cách giải: Ta dùng các quy tắc biến đổi bất phương trình để giải.
Giải
* Giải bất phương trình: \[ - 5x + 4 < 2 - 3x\]
\[ \Leftrightarrow - 5x + 3x < 2 - 4 \Leftrightarrow - 2x < - 2\]
\[ \Leftrightarrow x > - 2:\left( { - 2} \right) \Leftrightarrow x > 1\].
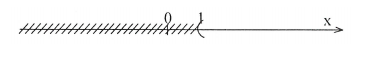
* Giải bất phương trình: \[8y - 5y + 4 < 3 + 2,5y\]
\[ \Leftrightarrow 8y - 5y - 2,5y < 3 - 4 \Leftrightarrow 0,5y < - 1\]
\[ \Leftrightarrow y < \left( { - 1} \right):0,5 \Leftrightarrow y < - 2\].
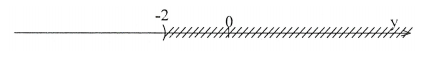
* Giải bất phương trình: \[8x - 3 \ge 1 - 6x + 15x\]
\[ \Leftrightarrow 8x + 6x - 15x \ge 1 + 3 \Leftrightarrow - x \ge 4\]
\[ \Leftrightarrow x \le 4:\left( { - 1} \right) \Leftrightarrow x \le - 4\].
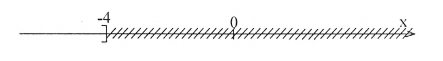
Ví dụ 3: Giải các bất phương trình:
a) \[5x - 7 > 3\left( {x - 2} \right) + 2x\];
b) \[4\left( {1,5x + 2,5} \right) < {\left( {x + 3} \right)^2} + \left( {5 - x} \right)\left( {x + 5} \right)\];
c) \[\frac{{x - 4}}{5} - x + 2 \le \frac{{x + 3}}{4} - \frac{{x - 2}}{3}\];
d) \[4x\left( {x - 1,25} \right) + \frac{{3\left( {1 - 3x} \right)}}{2} \ge {\left( {2x - 3} \right)^2}\].
* Tìm cách giải: Sử dụng các quy tắc biến đổi bất phương trình đưa các bất phương trình về dạng \[ax + b > 0\].
Giải
a) \[5x - 7 > 3\left( {x - 2} \right) + 2x \Leftrightarrow 5x - 7 > 3x - 6 + 2x\]
\[ \Leftrightarrow 5x - 3x - 2x > - 6 + 7 \Leftrightarrow 0x > 1\].
Bất phương trình vô nghiệm.
b) \[4\left( {1,5x + 2,5} \right) < {\left( {x + 3} \right)^2} + \left( {5 - x} \right)\left( {x + 5} \right)\]
\[ \Leftrightarrow 6x + 10 < {x^2} + 6x + 9 + 25 - {x^2} \Leftrightarrow 6x - 6x < 25 + 9 - 10\]
\[ \Leftrightarrow 0x < 24\] nghiệm đúng \[\forall x\].
Nghiệm của bất phương trình là \[x \in \mathbb{R}\].
c) \[\frac{{x - 4}}{5} - x + 2 \le \frac{{x + 3}}{4} - \frac{{x - 2}}{3}\]
\[ \Leftrightarrow 12\left( {x - 4} \right) - 60x + 120 \le 15\left( {x + 3} \right) - 20\left( {x - 2} \right)\]
\[ \Leftrightarrow 12x - 48 - 60x + 120 \le 15x + 45 - 20x + 40\]
\[ \Leftrightarrow 12x - 60x + 20x - 15x \le 45 - 120 + 40 + 48\]
\[ \Leftrightarrow - 43x \le 13 \Leftrightarrow x \ge - \frac{{13}}{{43}}\].
d) \[4x\left( {x - 1,25} \right) + \frac{{3\left( {1 - 3x} \right)}}{2} \ge {\left( {2x - 3} \right)^2}\]
\[ \Leftrightarrow 8x\left( {x - 1,25} \right) + 3\left( {1 - 3x} \right) \ge 2\left( {4{x^2} - 12x + 9} \right)\]
\[ \Leftrightarrow 8{x^2} - 10 + 3 - 9x \ge 8{x^2} - 24x + 18\]
\[ \Leftrightarrow 24x - 9x \ge 18 + 10 - 3 \Leftrightarrow 15x \ge 25 \Leftrightarrow x \ge \frac{5}{3}\].
Ví dụ 4: Tìm x sao cho: \[2\left( {3x - 4} \right) < 8x - 10 < 7x - 2\].
* Tìm cách giải: Giải bất phương trình kép này thực chất là giải đồng thời hai bất phương trình \[2\left( {3x - 4} \right) < 8x - 10\] và \[8x - 10 < 7x - 2\].
Giá trị của x thỏa mãn đồng thời cả hai bất phương trình là nghiệm.
Giải
\[2\left( {3x - 4} \right) < 8x - 10 < 7x - 2 \Leftrightarrow \left\{ \begin{array}{l}6x - 8 < 8x - 10\\8x - 10 < 7x - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x - 8x < 8 - 10\\8x - 7x < 10 - 2\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l} - 2x < - 2\\x < 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 2:\left( { - 2} \right)\\x < 8\end{array} \right. \Leftrightarrow 1 < x < 8\].
Ví dụ 5: Cho hai bất phương trình:
\[\frac{{x - 3}}{5} + \frac{{11 + x}}{4} > \frac{{3x - 5}}{2}{\rm{ }}\left( 1 \right)\] và \[5 + \frac{{x - 4}}{5} < x - \frac{{2x - 9}}{2} + \frac{{3x + 2}}{3}{\rm{ }}\left( 2 \right)\]
a) Tìm giá trị của x thỏa mãn hai bất phương trình.
b) Tìm giá trị nguyên của x thỏa mãn hai bất phương trình.
* Tìm cách giải: Yêu cầu của bài toán là tìm nghiệm và nghiệm nguyên chung của hai bất phương trình. Ta phải giải hai bất phương trình rồi tìm các giá trị nguyên của nghiệm trong khoảng nghiệm chung của hai bất phương trình.
Giải
Giải bất phương trình (1): \[\frac{{x - 3}}{5} + \frac{{11 + x}}{4} > \frac{{3x - 5}}{2}\]
\[ \Leftrightarrow 4\left( {x - 3} \right) + 5\left( {11 + x} \right) > 10\left( {3x - 5} \right)\]
\[ \Leftrightarrow 4x - 12 + 55 + 5x > 30x - 50 \Leftrightarrow 9x - 30x > - 50 - 55 + 12\]
\[ \Leftrightarrow - 21x > - 93 \Leftrightarrow x < \frac{{93}}{{21}}\]
Giải bất phương trình (2): \[5 + \frac{{x - 4}}{5} < x - \frac{{2x - 9}}{2} + \frac{{3x + 2}}{3}\]
\[ \Leftrightarrow 150 + 6\left( {x - 4} \right) < 30x - 15\left( {2x - 9} \right) + 10\left( {3x + 2} \right)\]
\[ \Leftrightarrow 150 + 6x - 24 < 30x - 30x + 135 + 30x + 20\]
\[ \Leftrightarrow 6x - 30x < - 150 + 24 + 135 + 20\]
\[ \Leftrightarrow - 24x < 29 \Leftrightarrow x > - \frac{{29}}{{24}}\].
a) Giá trị của x thỏa mãn hai bất phương trình là \[ - \frac{{29}}{{24}} < x < \frac{{93}}{{21}}\]
b) Giá trị nguyên của x thỏa mãn hai bất phương trình là:
\[x \in \left\{ { - 1;0;1;2;3;4} \right\}\].
Ví dụ 6: Cho \[A = \frac{{{x^2} + 6x + 9}}{{{x^3} + 27}}:\frac{{ - {x^3} + 3{x^2} + 9x - 27}}{{{x^2} - 6x + 9}}\]
Rút gọn biểu thức A rồi tìm giá trị của x để \[A < 0\].
* Tìm cách giải: Bài toán yêu cầu từ kết quả rút gọn A giải bất phương trình \[A < 0\]. Lưu ý ĐKXĐ của A và các hằng đẳng thức.
Giải
ĐKXĐ: \[x \ne \pm 3\]
\[A = \frac{{{{\left( {x + 3} \right)}^2}}}{{\left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right)}}.\frac{{{{\left( {x - 3} \right)}^2}}}{{\left( {{x^2} - 9} \right)\left( {3 - x} \right)}} = \frac{{ - 1}}{{{x^2} - 3x + 9}}\]
Do \[{x^2} - 3x + 9 = \left( {{x^2} - 2.x.\frac{3}{2} + \frac{9}{4}} \right) + \frac{{27}}{4} = {\left( {x - \frac{3}{2}} \right)^2} + \frac{{27}}{4} > 0,\forall x\].
Do đó \[A < 0\] với \[x \ne \pm 3\].
Ví dụ 7: Giải bất phương trình sau với a, b là các hằng số dương.
\[a - {a^2}x > b - {b^2}x\]
* Tìm cách giải: Bất phương trình bậc nhất có hệ số bằng chữ. Khi giải lưu ý biện luận cho hệ số của ẩn.
Giải
a) \[ \Leftrightarrow a - {a^2}x > b - {b^2}x \Leftrightarrow \left( {{b^2} - {a^2}} \right)x > b - a\]
\[ \Leftrightarrow \left( {b - a} \right)\left( {b + a} \right)x > b - a{\rm{ }}\left( 1 \right)\]
Nếu \[b > a\] thì \[b - a > 0\]. Nghiệm của bất phương trình là \[x > \frac{1}{{b + a}}\];
Nếu \[b < a\] thì \[b - a < 0\]. Nghiệm của bất phương trình là \[a < \frac{1}{{b + a}}\];
Nếu \[b = a\] thì (1) trở thành \[0x > 0\] bất phương trình vô nghiệm.
Ví dụ 8: Tìm giá trị của m để phương trình sau có nghiệm dương
\[\frac{{2\left( {x - m} \right)}}{{2 - m}} - \frac{{x - 2}}{{2 + m}} = \frac{{x + 2}}{{2 - m}} - \frac{{x + m}}{{2 + m}}{\rm{ }}\left( {m \ne \pm 2} \right){\rm{ }}\left( 1 \right)\]
* Tìm cách giải: Ta giải phương trình có hệ số bằng chữ lại nằm ở mẫu, do đó đặc biệt lưu ý ĐKXĐ và sau khi tìm nghiệm lập luận để có nghiệm dương.
Giải
(1) biến đổi thành \[2\left( {x - m} \right)\left( {2 + m} \right) - \left( {2 - m} \right)\left( {x - 2} \right) = \left( {x + 2} \right)\left( {2 + m} \right) - \left( {x + m} \right)\left( {2 - m} \right)\]
\[ \Leftrightarrow 4x + 2mx - 4m - 2{m^2} - 2x + mx + 4 - 2m = 2x + mx + 4 + 2m - 2x + mx - 2m + {m^2}\]
\[ \Leftrightarrow 2x + mx = 3{m^2} + 6m \Leftrightarrow x\left( {m + 2} \right) = 3m\left( {m + 2} \right)\]
Với \[m \ne - 2\] thì \[m + 2 \ne 0\] ta có \[x = 3m\]
Để \[x > 0\] thì \[3m > 0\] hay \[m > 0\].
Vậy với \[m > 0\] và \[m \ne - 2\] thì phương trình có nghiệm dương.
Ví dụ 9: Giải các bất phương trình:
a) \[\frac{{2x - 1016}}{{1000}} + \frac{{2x - 1000}}{{1016}} < \frac{{2x - 16}}{{2000}} + \frac{{2x - 1}}{{2015}}{\rm{ }}\left( 1 \right)\]
b) \[\frac{{5x - 100}}{{900}} + \frac{{5x - 200}}{{800}} \le \frac{{5x - 500}}{{250}}{\rm{ }}\left( 2 \right)\]
* Tìm cách giải: a) Thêm \[\left( { - 1} \right)\] vào mỗi hạng tử ở hai vế rồi quy đồng mẫu từng cặp ta thấy xuất hiện nhân tử chung \[2x - 2016\]. b) Thêm \[\left( { - 1} \right)\] vào mỗi hạng tử ở vế trái, thêm \[\left( { - 2} \right)\] vào vế phải rồi quy đồng mẫu từng cặp ta thấy xuất hiện nhân tử chung \[5x - 1000\]. Ta có cách giải sau:
Giải
a) \[\left( 1 \right) \Leftrightarrow \frac{{2x - 1016}}{{1000}} - 1 + \frac{{2x - 1000}}{{1016}} - 1 < \frac{{2x - 16}}{{2000}} - 1 + \frac{{2x - 1}}{{2015}} - 1\]
\[ \Leftrightarrow \frac{{2x - 2016}}{{1000}} + \frac{{2x - 2016}}{{1016}} < \frac{{2x - 2016}}{{2000}} + \frac{{2x - 2016}}{{2015}}\]
\[ \Leftrightarrow \left( {2x - 2016} \right)\left( {\frac{1}{{1000}} + \frac{1}{{1016}} - \frac{1}{{2000}} - \frac{1}{{2015}}} \right) < 0\]
Do \[\frac{1}{{1000}} + \frac{1}{{1016}} - \frac{1}{{2000}} - \frac{1}{{2015}} > 0\] nên \[2x - 2016 < 0 \Leftrightarrow 2x < 2016\]
\[ \Leftrightarrow x < 1008\].
b) \[\left( 2 \right) \Leftrightarrow \frac{{5x - 100}}{{900}} - 1 + \frac{{5x - 200}}{{800}} - 1 \le \frac{{5x - 600}}{{200}} - 2\]
\[ \Leftrightarrow \frac{{5x - 1000}}{{900}} + \frac{{5x - 1000}}{{800}} - \frac{{5x - 1000}}{{200}} \le 0 \Leftrightarrow \left( {5x - 1000} \right)\left( {\frac{1}{{900}} + \frac{1}{{800}} - \frac{1}{{200}}} \right) \le 0\]
Do \[\frac{1}{{900}} + \frac{1}{{800}} - \frac{1}{{200}} = - \frac{{19}}{{7200}} < 0\]
Nên \[5x - 1000 \ge 0 \Leftrightarrow x \ge 200\].
III. Bài tập vận dụng
22.1. Tìm các giá trị nguyên của x để biểu thức \[A = \frac{{x - 1}}{2} - \frac{{x - 2}}{3}\] có giá trị lớn hơn 4 nhưng nhỏ hơn 5.
Hướng dẫn giải – đáp số
Cách 1: Ta giải bất phương trình kép
\[4 < \frac{{x - 1}}{2} - \frac{{x - 2}}{3} < 5 \Leftrightarrow \left\{ \begin{array}{l}\frac{{x - 1}}{2} - \frac{{x - 2}}{3} > 4\\\frac{{x - 1}}{2} - \frac{{x - 2}}{3} < 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 23\\x < 29\end{array} \right.\]
Các giá trị nguyên của x thỏa mãn \[23 < x < 29\] là \[x \in \left\{ {24;25;26;27;28} \right\}\]
Cách 2: \[4 < \frac{{x - 1}}{2} - \frac{{x - 2}}{3} < 5 \Leftrightarrow 24 < 3\left( {x - 1} \right) - 2\left( {x - 2} \right) < 30\]
\[ \Leftrightarrow 24 < x + 1 < 30 \Leftrightarrow 23 < x < 29\] và cũng có kết quả trên.
22.2. Giải các bất phương trình:
a) \[3x - 2 > 5\left( {x - 2} \right) + 2\left( {3 - x} \right)\];
b) \[5{\left( {x + 2} \right)^2} < \left( {2x + 3} \right)\left( {2x - 3} \right) + {\left( {x - 5} \right)^2} + 30x\];
c) \[4\left( {2,5{x^2} + 1} \right) \ge 9\left( {x + 3} \right)\left( {x - 3} \right) + {\left( {2 - x} \right)^2} + 1\];
d) \[{x^3} \le 2x + 56\].
Hướng dẫn giải – đáp số
Sử dụng các quy tắc biến đổi bất phương trình đưa các bất phương trình về dạng \[ax + b > 0\].
a) \[3x - 2 > 5\left( {x - 2} \right) + 2\left( {3 - x} \right) \Leftrightarrow 0x > - 2\] nghiệm đúng \[\forall x\].
Nghiệm của bất phương trình là \[x \in \mathbb{R}\].
b) \[5{\left( {x + 2} \right)^2} < \left( {2x + 3} \right)\left( {2x - 3} \right) + {\left( {x - 5} \right)^2} + 30x \Leftrightarrow 0x < - 4\]
Bất phương trình vô nghiệm.
c) \[4\left( {2,5{x^2} + 1} \right) \ge 9\left( {x + 3} \right)\left( {x - 3} \right) + {\left( {2 - x} \right)^2} + 1 \Leftrightarrow 4x \ge - 80\]
\[ \Leftrightarrow x \ge - 20\]
d) Thêm vào hai vế \[ - 64\] làm xuất hiện dạng \[{x^3} - {4^3}\] ở vế trái và \[2\left( {x - 4} \right)\] ở vế phải.
Ta có \[{x^3} \le 2x + 56 \Leftrightarrow {x^3} - 64 \le 2x + 56 - 64\]
\[ \Leftrightarrow \left( {x - 4} \right)\left( {{x^2} + 4x + 16} \right) - 2\left( {x - 4} \right) \le 0 \Leftrightarrow \left( {x - 4} \right)\left( {{x^2} + 4x + 14} \right) \le 0\]
Do \[{x^2} + 4x + 14 = {\left( {x + 2} \right)^2} + 10 > 0,{\rm{ }}\forall x\] nên ta có \[x - 4 \le 0\] hay \[x \le 4\].
22.3. Giải bất phương trình:
\[\frac{{x + 1}}{2} + \frac{{x + 2}}{3} > \frac{{x + 3}}{4} + \frac{{x + 4}}{5}\]
Hướng dẫn giải – đáp số
\[\frac{{x + 1}}{2} + \frac{{x + 2}}{3} > \frac{{x + 3}}{4} + \frac{{x + 4}}{5}\]
\[ \Leftrightarrow 30\left( {x + 1} \right) + 20\left( {x + 2} \right) > 15\left( {x + 3} \right) + 12\left( {x + 4} \right)\]
\[ \Leftrightarrow 23x > 23 \Leftrightarrow x > 1\].
* Chú ý: d) Nhận xét: Nếu thêm \[\left( { - 1} \right)\] vào mỗi hạng tử ở hai vế rồi quy đồng từng cặp ta thấy xuất hiện nhân tử chung là \[\left( {x - 1} \right)\]. Do đó còn cách sau:
\[\frac{{x + 1}}{2} + \frac{{x + 2}}{3} > \frac{{x + 3}}{4} + \frac{{x + 4}}{5}\]
\[ \Leftrightarrow \left( {\frac{{x + 1}}{2} - 1} \right) + \left( {\frac{{x + 2}}{3} - 1} \right) > \left( {\frac{{x + 3}}{4} - 1} \right) + \left( {\frac{{x + 4}}{5} - 1} \right)\]
\[ \Leftrightarrow \left( {x - 1} \right)\left( {\frac{1}{2} + \frac{1}{3} - \frac{1}{4} - \frac{1}{5}} \right) > 0 \Leftrightarrow x > 1\] do \[\left( {\frac{1}{2} + \frac{1}{3} - \frac{1}{4} - \frac{1}{5}} \right) > 0\].
22.4. Tìm giá trị của x thỏa mãn bất phương trình:
a) \[\frac{{x + 2}}{3} - 5 > \frac{{2\left( {x - 1} \right)}}{4} - x{\rm{ }}\left( 1 \right)\] và \[\frac{{{x^2}}}{3} - \frac{{2x - 3}}{6} < \frac{{{{\left( {2x - 1} \right)}^2}}}{{12}} + x{\rm{ }}\left( 2 \right)\].
b) \[\frac{{2x - 1}}{5} - \frac{x}{2} \le \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{{10}}{\rm{ }}\left( 3 \right)\] và \[2x\left( {x - 5} \right) + x\left( {x - 2} \right) > 3\left( {x + 4} \right)\left( {x - 4} \right) - 12{\rm{ }}\left( 4 \right)\].
Hướng dẫn giải – đáp số
a) Giải bất phương trình (1) ta có \[x > 4,6\]. Giải bất phương trình (2) ta có \[x > \frac{5}{{12}}\]. Giá trị \[x > 4,6\] thỏa mãn cả hai bất phương trình.
b) Giải bất phương trình (3) ta có \[x \ge - 1\]. Giải bất phương trình (4) ta có \[x < 5\]. Giá trị \[ - 1 \le x < 5\] thỏa mãn cả hai bất phương trình.
22.5. Tìm số nguyên x thỏa mãn cả hai bất phương trình:
a) \[3\left( {2x - 5} \right) > 2\left( {6 - 7x} \right){\rm{ }}\left( 1 \right)\] và \[\frac{{2\left( {x - 1} \right)}}{3} \le \frac{{x + 1}}{5} + \frac{1}{{15}}{\rm{ }}\left( 2 \right)\]
b) \[\frac{{x - 1}}{3} - 1 \le \frac{{2x - 3}}{4}{\rm{ }}\left( 3 \right)\] và \[4\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) \ge \left( {4{x^2} + 3} \right)x - 16{\rm{ }}\left( 4 \right)\].
Hướng dẫn giải – đáp số
a) Giải bất phương trình (1) ta có \[x > \frac{{27}}{{20}}\]. Giải bất phương trình (2) ta có \[x \le 2\]. Giá trị \[x = 2\] thỏa mãn cả hai bất phương trình.
b) Giải bất phương trình (3) ta có \[x \ge - 3,5\]. Giải bất phương trình (4) ta có \[x \le 4\]. Vậy \[x \in \left\{ { - 3; - 2; - 1;0;1;2;3;4} \right\}\].
22.6. Tìm giá trị nguyên của x để \[3\left( {x - 1} \right) - 4 < \frac{{3x - 11}}{5} < \frac{{2 + 5x}}{4} - 2\].
Hướng dẫn giải – đáp số
Giải từng bất phương trình ta có:
\[3\left( {x - 1} \right) - 4 < \frac{{3x - 11}}{5} \Leftrightarrow 15x - 15 - 20 < 3x - 11 \Leftrightarrow 12x < 24 \Leftrightarrow x < 2\]
\[\frac{{3x - 11}}{5} < \frac{{2 + 5x}}{4} - 2 \Leftrightarrow 12x - 44 < 10 + 25x - 40 \Leftrightarrow - 13x < 14 \Leftrightarrow x > - \frac{{14}}{{13}}\]
Do đó \[ - \frac{{14}}{{13}} < x < 2\]. Các giá trị nguyên của x thỏa mãn là \[x \in \left\{ { - 1;0;1} \right\}\].
22.7. Cho biểu thức \[A = \left( {\frac{{2x}}{5} + \frac{5}{{2x - 5}}} \right):\left( {\frac{{4{x^2}}}{{125 - 20{x^2}}} + \frac{1}{{2x + 5}}} \right)\]
a) Rút gọn biểu thức A;
b) Tìm x để \[A \le - 2\];
c) Tìm x để \[A > ax\] với a là một hằng số.
Hướng dẫn giải – đáp số
Sau khi rút gọn biểu thức A ta giải bất phương trình \[A \le - 2\] và phương trình chứa tham số \[A > ax\]. Ta đặc biệt lưu ý ĐKXĐ của A và biện luận khi giải bất phương trình chứa tham số.
a) ĐKXĐ: \[x \ne \pm 2,5\]
\[A = \frac{{4{x^2} - 10x + 25}}{{5\left( {2x - 5} \right)}}.\frac{{5\left( {2x + 5} \right)\left( {5 - 2x} \right)}}{{4{x^2} - 10x + 25}} = - \left( {2x + 5} \right)\]
b) Để \[A \le - 2\] ta có: \[ - \left( {2x + 5} \right) \le - 2 \Leftrightarrow 2x + 5 \ge 2 \Leftrightarrow 2x \ge - 3\]
\[ \Leftrightarrow x \ge - 1,5\].
c) \[A > ax\] tức là \[ - 2x - 5 > ax \Leftrightarrow ax + 2x < - 5 \Leftrightarrow \left( {a + 2} \right)x < - 5\]
Nếu \[a > - 2\] thì \[x < \frac{{ - 5}}{{a + 2}}\]; Nếu \[a < - 2\] thì \[x > \frac{{ - 5}}{{a + 2}}\];
Nếu \[a = - 2\] ta có \[0x < - 5\] vô lý.
22.8. Tìm giá trị của a để nghiệm của phương trình \[\frac{{{a^2} - 4}}{{2x - 5}} = 2 + a\] là số dương nhưng nhỏ hơn 2.
Hướng dẫn giải – đáp số
ĐKXĐ: \[x \ne 2,5\] ta có \[\frac{{{a^2} - 4}}{{2x - 5}} = 2 + a\]
\[ \Leftrightarrow \left( {a - 2} \right)\left( {a + 2} \right) - \left( {2 + a} \right)\left( {2x - 5} \right) = 0 \Leftrightarrow \left( {a + 2} \right)\left( {a - 2x + 3} \right) = 0\]
Nếu \[a \ne - 2\] thì \[a - 2x + 3 = 0 \Leftrightarrow x = \frac{{a + 3}}{2}\]
\[x > 0\] thì \[a + 3 > 0 \Leftrightarrow a > - 3\]
\[x < 2\] thì \[\frac{{a + 3}}{2} < 2 \Leftrightarrow a + 3 < 4 \Leftrightarrow a < 1\].
Vậy để nghiệm của bất phương trình sau là số dương nhưng nhỏ hơn 2: \[ - 3 < a < 1\] và \[a \ne - 2\].
(Nếu \[a = - 2\] thì ta có \[0x = 0\] phương trình có vô số nghiệm do đó có vô số nghiệm dương trừ \[x = 2,5\]).
22.9. Giải các bất phương trình với \[a,b\] là các hằng số \[\left( {a \ne 0} \right)\].
a) \[a\left( {x - a} \right) > 5\left( {x - 5} \right)\]; b) \[\frac{{ax - b}}{a} + \left( {a + b + 1} \right)x > \frac{{2b}}{a}\].
Hướng dẫn giải – đáp số
a) \[a\left( {x - a} \right) > 5\left( {x - 5} \right) \Leftrightarrow ax - {a^2} > 5x - 25\]
\[ \Leftrightarrow \left( {a - 5} \right)x > \left( {a - 5} \right)\left( {a + 5} \right)\]
Nếu \[a > 5\] thì nghiệm của bất phương trình là \[x > a + 5\]
Nếu \[a < 5\] thì nghiệm của bất phương trình là \[x < a + 5\]
Nếu \[a = 5\] thì bất phương trình trở thành \[0x > 0\], vô nghiệm.
b) Biến đổi bất phương trình ta có:
\[x + \left( {a + b + 1} \right)x > \frac{b}{a} + \frac{{2b}}{a} \Leftrightarrow \left( {a + b + 2} \right)x > \frac{{3b}}{a}\]
* Nếu \[a + b + 2 > 0\] thì \[x > \frac{{3b}}{{a\left( {a + b + 2} \right)}}\]
* Nếu \[a + b + 2 < 0\] thì \[x < \frac{{3b}}{{a\left( {a + b + 2} \right)}}\]
* Nếu \[a + b + 2 = 0\] thì \[0x > \frac{{3b}}{a}\] khi ấy:
Nếu \[ab \ge 0\]: Vô nghiệm. Nếu \[ab < 0\]: Vô số nghiệm.
22.10. Giải bất phương trình:
\[\frac{{5x + 1015}}{{1000}} + \frac{{5x + 1000}}{{1015}} + \frac{{5x + 1}}{{2014}} > \frac{{5x - 1}}{{2016}} + \frac{{5x - 2}}{{2017}} + \frac{{5x - 10}}{{2025}}\]
Hướng dẫn giải – đáp số
Thêm 1 vào mỗi hạng tử ở hai vế rồi quy đồng mẫu từng cặp ta thấy xuất hiện nhân tử chung \[2x + 2015\]. Ta có cách giải:
\[\frac{{5x + 1015}}{{1000}} + \frac{{5x + 1000}}{{1015}} + \frac{{5x + 1}}{{2014}} > \frac{{5x - 1}}{{2016}} + \frac{{5x - 2}}{{2017}} + \frac{{5x - 10}}{{2025}}\]
\[ \Leftrightarrow \frac{{5x + 1015}}{{1000}} + 1 + \frac{{5x + 1000}}{{1015}} + 1 + \frac{{5x + 1}}{{2014}} + 1 > \frac{{5x - 1}}{{2016}} + 1 + \frac{{5x - 2}}{{2017}} + 1 + \frac{{5x - 10}}{{2025}} + 1\]
\[ \Leftrightarrow \left( {5x + 2015} \right)\left( {\frac{1}{{1000}} + \frac{1}{{1015}} + \frac{1}{{2014}} - \frac{1}{{2016}} - \frac{1}{{2017}} - \frac{1}{{2025}}} \right) > 0\]
Do \[\frac{1}{{1000}} + \frac{1}{{1015}} + \frac{1}{{2014}} - \frac{1}{{2016}} - \frac{1}{{2017}} - \frac{1}{{2025}} > 0\]
Nên \[5x + 2015 > 0 \Leftrightarrow 5x > - 2015 \Leftrightarrow x > - 403\].
22.11. Cho \[A = \frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{9.11}}\]
\[B = \left( {1 + \frac{1}{{1.3}}} \right)\left( {1 + \frac{1}{{2.4}}} \right)...\left( {1 + \frac{1}{{8.10}}} \right)\left( {1 + \frac{1}{{9.11}}} \right)\]
Tìm số nguyên x thỏa mãn \[2A < \frac{{2x}}{{11}} < B\].
Hướng dẫn giải – đáp số
\[2A = \frac{2}{{1.3}} + \frac{2}{{3.5}} + \frac{2}{{5.7}} + ... + \frac{2}{{9.11}} = 1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + \frac{1}{5} - \frac{1}{7} + ... + \frac{1}{9} - \frac{1}{{11}} = \frac{{10}}{{11}}\]
\[B = \left( {1 + \frac{1}{{1.3}}} \right)\left( {1 + \frac{1}{{2.4}}} \right)...\left( {1 + \frac{1}{{8.10}}} \right)\left( {1 + \frac{1}{{9.11}}} \right) = \frac{{{2^2}}}{{1.3}}.\frac{{{3^2}}}{{2.4}}.....\frac{{{9^2}}}{{8.10}}.\frac{{{{10}^2}}}{{9.11}} = \frac{{20}}{{11}}\]
\[2A < \frac{{2x}}{{11}} < B\] tức là \[\frac{{10}}{{11}} < \frac{{2x}}{{11}} < \frac{{20}}{{11}} \Leftrightarrow 10 < 2x < 20 \Leftrightarrow 5 < x < 10\]
Do đó \[x \in \left\{ {6;7;8;9} \right\}\].
22.12. Một đội bóng đá tham gia một giải đấu. Đội đấu 20 trận và được 41 điểm. Theo quy định của giải, mỗi trận thắng được 3 điểm, mỗi trận hòa được 1 điểm, mỗi trận thua 0 điểm. Gọi số trận thắng của đội đó là x, số trận hòa là y và số trận thua là z, tìm \[x,y,z\]. Biết rằng số trận thắng của đội đó là một số chẵn.
Hướng dẫn giải – đáp số
Ta lập các phương trình biểu thị tổng số trận và tổng số điểm, xét xem x bị chặn bởi hai giá trị nào. Từ đó tìm ra các giá trị của x và y, z.
* Gọi số trận thắng của đội đó là x, số trận hòa là y và số trận thua là z \[\left( {x,y,z \in \mathbb{N}} \right)\]. Ta có \[x + y + z = 20{\rm{ }}\left( 1 \right)\]; đồng thời \[3.x + 1.y + 0.z = 41{\rm{ }}\left( 2 \right)\].
Từ (2) ta có \[3x + y = 41\] suy ra \[3x \le 41 \Leftrightarrow x \le \frac{{41}}{3} = 13\frac{2}{3}\]
Từ (1) và (2) \[ \Rightarrow 2x - z = 21 \Rightarrow 2x \ge 21 \Leftrightarrow x \ge \frac{{21}}{2} = 10\frac{1}{2}\]
Như vậy \[10\frac{1}{2} \le x \le 13\frac{2}{3}\]. Do \[x \in \mathbb{N} \Rightarrow x = 11;12;13\].
Do x là số chẵn nên \[x = 12\]. Từ đó có \[3.12 + y = 41 \Rightarrow y = 5\] và \[z = 3\].
22.13. Ký hiệu \[\left[ a \right]\] (phần nguyên của a) là số nguyên lớn nhất không vượt quá a.
Tìm \[x \in \mathbb{Z}\] biết rằng \[\left[ {\frac{{8x - 3}}{5}} \right] = 2x + 1\].
Hướng dẫn giải – đáp số
Do \[\left[ a \right]\] là số nguyên lớn nhất không vượt quá a nên nếu \[\left[ a \right] = n\] thì n là số nguyên và \[0 \le a - n < 1\].
Vì thế \[\left[ {\frac{{8x - 3}}{5}} \right] = 2x + 1 \Leftrightarrow \left\{ \begin{array}{l}0 \le \frac{{8x - 3}}{5} - \left( {2x + 1} \right) < 1\\\left( {2x + 1} \right) \in \mathbb{Z}\end{array} \right.\]
Xét \[0 \le \frac{{8x - 3}}{5} - \left( {2x + 1} \right) < 1 \Leftrightarrow 0 \le 8x - 3 - 10x - 5 < 5\]
\[ \Leftrightarrow 0 \le - 2x - 8 < 5 \Leftrightarrow 8 \le - 2x < 13 \Leftrightarrow - 8 \ge 2x > - 13\]
\[ \Leftrightarrow - 7 \ge 2x + 1 > - 12\]
Do \[2x + 1 \in \mathbb{Z}\] và \[2x + 1\] là số lẻ nên \[2x + 1 = - 7 \Leftrightarrow x = - 4\].
\[2x + 1 = - 9 \Leftrightarrow x = - 5;{\rm{ }}2x + 1 = - 11 \Leftrightarrow x = - 6\].
Vậy \[x \in \left\{ { - 4; - 5; - 6} \right\}\]
22.14. Giải bất phương trình \[\frac{{x + 1}}{{2002}} - 2 > \frac{{x + 4}}{{1999}} + \frac{{x + 5}}{{1998}} + \frac{{x + 7}}{{1996}}\].
(Đề thi chọn học sinh giỏi lớp 8 huyện Thường Tín – Hà Tây (cũ) năm học 2002 – 2003)
Hướng dẫn giải – đáp số
\[\frac{{x + 1}}{{2002}} - 2 > \frac{{x + 4}}{{1999}} + \frac{{x + 5}}{{1998}} + \frac{{x + 7}}{{1996}}\]
\[ \Leftrightarrow \frac{{x + 1}}{{2002}} + 1 > \left( {\frac{{x + 4}}{{1999}} + 1} \right) + \left( {\frac{{x + 5}}{{1998}} + 1} \right) + \left( {\frac{{x + 7}}{{1996}} + 1} \right)\]
\[ \Leftrightarrow \frac{{x + 2003}}{{2002}} > \frac{{x + 2003}}{{1999}} + \frac{{x + 2003}}{{1998}} + \frac{{x + 2003}}{{1996}}\]
\[ \Leftrightarrow \left( {x + 2003} \right)\left( {\frac{1}{{2002}} - \frac{1}{{1999}} - \frac{1}{{1998}} - \frac{1}{{1996}}} \right) > 0\]
Do \[\frac{1}{{2002}} - \frac{1}{{1999}} - \frac{1}{{1998}} - \frac{1}{{1996}} < 0\] nên \[x + 2003 < 0 \Leftrightarrow x < - 2003\].
22.15. Giải bất phương trình \[x + \left| {x - 1} \right| > 5\].
(Thi vào lớp 10 Quốc học Huế, năm 2003 – 2004)
Hướng dẫn giải – đáp số
* Với \[x \ge 1\] thì \[\left| {x - 1} \right| = x - 1\]. Bất phương trình trở thành \[x + x - 1 > 5 \Leftrightarrow 2x > 6 \Leftrightarrow x > 3\] (thỏa mãn).
* Với \[x < 1\] thì \[\left| {x - 1} \right| = 1 - x\]. Bất phương trình trở thành \[x + 1 - x > 5 \Leftrightarrow 0x > 4\] vô nghiệm.
Vậy nghiệm của bất phương trình là \[x > 3\].
Xem thêmTừ khóa » Giải Bất Phương Trình Bậc Nhất Một ẩn
-
Giải Bất Phương Trình Bậc Nhất Một Ẩn Lớp 8 - Kiến Guru
-
Bất Phương Trình Bậc Nhất Một ẩn
-
Bất Phương Trình Bậc Nhất Một ẩn - Toán 8
-
Giải Bất Phương Trình Bậc Nhất Một ẩn
-
Giải Toán 8 Bài 4: Bất Phương Trình Bậc Nhất Một ẩn
-
Bất Phương Trình Bậc Nhất Một ẩn - Lý Thuyết Và Cách Giải Bài Tập
-
Bất Phương Trình Bậc Nhất Một ẩn – Lý Thuyết & Bài Tập - I Toán - Itoan
-
2 Cách Giải Bất Phương Trình Bậc Nhất Một ẩn (có Ví Dụ)
-
Giải Toán 8 Bài 4. Bất Phương Trình Bậc Nhất Một ẩn
-
Chuyên đề: Bất Phương Trình Bậc Nhất Một ẩn - Toán Lớp 8
-
Chuyên đề Bất Phương Trình Bậc Nhất Một ẩn - Toán THCS
-
Bất Phương Trình Bậc Nhất Một ẩn Là Gì? - TopLoigiai
-
Bất Phương Trình Bậc Nhất Một ẩn
-
Bất Phương Trình Bậc Nhất Một ẩn - Bài 4 - Toán Học 8 - YouTube