Bất Phương Trình Logarit - Tự Học 365

Bất phương trình logarit

Thông hiểu (40.8%)

Nhận biết (34.7%)

Vận dụng (20.4%)

Vận dụng cao (4.1%)

• 1 Làm xong biết đáp án, phương pháp giải chi tiết.
• 2 Học sinh có thể hỏi và trao đổi lại nếu không hiểu.
• 3 Xem lại lý thuyết, lưu bài tập và note lại các chú ý
• 4 Biết điểm yếu và có hướng giải pháp cải thiện

Lựa chọn loại câu hỏi bạn muốn làm Làm tất cả Làm bài dễ Làm bài khó

Bạn sẽ không thể làm bài nếu chưa đăng nhập. Đăng nhập ngay !

Danh sách câu hỏi

Bất phương trình \(\log_{{\frac{4}{{25}}}}(x + 1) \ge \log_{{\frac{2}{5}}}x\) tương đương với bất phương trình nào dưới đây?

Bất phương trình \({\log _2}\left( {3x - 2} \right) > {\log _2}\left( {6 - 5x} \right)\) có tập nghiệm là:

Giải bất phương trình $\log_{2}\left( {3x-1} \right) \ge 3$.

Để giải bất phương trình \(\ln \dfrac{{2x}}{{x - 1}} > 0\,\,\,\left( * \right)\), một học sinh lập luận qua ba bước như sau:

Bước 1: Điều kiện \(\dfrac{{2x}}{{x - 1}} > 0 \Leftrightarrow \left[ \begin{array}{l}x < 0\\x > 1\end{array} \right.\,\,\,\,\left( 1 \right)\)

Bước 2: Ta có: \(\ln \dfrac{{2x}}{{x - 1}} > 0 \Leftrightarrow \ln \dfrac{{2x}}{{x - 1}} > \ln 1 \Leftrightarrow \dfrac{{2x}}{{x - 1}} > 1\,\,\,\,\left( 2 \right)\)

Bước 3: \(\left( 2 \right) \Leftrightarrow 2x > x - 1 \Leftrightarrow x > - 1\,\,\,\,\left( 3 \right)\)

Kết hợp (3) và (1) ta được: \(\left[ \begin{array}{l} - 1 < x < 0\\x > 1\end{array} \right.\)

Vậy tập nghiệm của bất phương trình là \(\left( { - 1;0} \right) \cup \left( {1; + \infty } \right)\)

Hỏi lập luận trên là đúng hay sai ? Nếu sai thì sai từ bước nào ?

Giải bất phương trình \({\log _{\frac{1}{3}}}(x + {9^{500}}) > - 1000\)

Tập nghiệm của bất phương trình ${\log _{\frac{1}{2}}}\left( {2x - 1} \right) > - 1$ là

Nghiệm của bất phương trình ${\log _{\frac{1}{2}}}\left( {x - 3} \right) \ge 2$.

Số nguyên nhỏ nhất thỏa mãn $\log_{2}\left( {5x-3} \right) > 5$ là:

Tập nghiệm của bất phương trình ${\log _{0,5}}x > {\log _{0,5}}2$ là:

Trong phim Cube của đạo diễn Vincenzo Natali thực hiện năm 1997, có một căn phòng âm thanh.Trong căn phòng đó, cứ có bất kỳ âm thanh nào phát ra với mức cường độ âm thanh trên \(50dB\) thì có một bộ phận trong căn phòng sẽ phát ra khí độc giết chết toàn bộ sự sống trong đó. Biết rằng mức cường độ âm thanh được tính theo công thức \(L = 10\log \dfrac{I}{{{I_0}}}\) (đơn vị: \(dB\)), trong đó \({I_0} = {10^{ - 12}}W/{m^2}\) là cường độ âm chuẩn, \(I\) là cường độ âm. Tính giá trị lớn nhất \({I_{\max }}\) của cường độ âm \(I\) để căn phòng an toàn.

Tìm tập nghiệm \(S\) của bất phương trình \({\log _{\frac{1}{2}}}\left( {x - 1} \right) > {\log _{\frac{1}{2}}}\left( {5 - 2x} \right)\).

Tìm tập nghiệm S của bất phương trình ${\log _{\frac{1}{2}}}\left( {x - 3} \right) \ge {\log _{\frac{1}{2}}}4$.

Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\) nghiệm đúng với mọi giá trị \(x \in \left[ {1;64} \right]\).

Tập nghiệm của bất phương trình $\ln\left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0$ là:

Tập nghiệm của bất phương trình ${\log _{\sqrt 3 }}x + {\log _{\sqrt[4]{3}}}x + {\log _{\sqrt[6]{3}}}x + ... + {\log _{\sqrt[{16}]{3}}}x < 36$ là:

Tập nghiệm của bất phương trình $\log\left( {{x^2} + 25} \right) > \log\left( {10x} \right)$ là:

Tập nghiệm của bất phương trình $3{\log _2}\left( {x + 3} \right) - 3 \le {\log _2}{\left( {x + 7} \right)^3} - {\log _2}{\left( {2 - x} \right)^3}$ là $S = \left( {a;{\rm{ }}b} \right)$. Tính $P = b - a$.

Tập nghiệm của bất phương trình $({2^{{x^2} - 4}} - 1).\ln {x^2} < 0$ là:

Số nghiệm nguyên của phương trình \(\left( {x - 3} \right)\left( {1 + logx} \right) < 0\) là:

Giải bất phương trình \({\log _3}({2^x} - 3) < 0\)

Giải bất phương trình sau ${\log _{\frac{1}{5}}}\left( {3x - 5} \right) > {\log _{\frac{1}{5}}}\left( {x + 1} \right)$

Bất phương trình ${\log _4}\left( {x + 7} \right) > {\log _2}\left( {x + 1} \right)$ có bao nhiêu nghiệm nguyên?

Nghiệm của bất phương trình ${\log _2}(x + 1) + {\log _{\frac{1}{2}}}\sqrt {x + 1} \le 0$ là :

Bất phương trình ${\log _{\frac{1}{2}}}\left( {3x - 2} \right) > \dfrac{1}{2}{\log _{\frac{1}{2}}}{\left( {22 - 5x} \right)^2}$ có bao nhiêu nghiệm nguyên?

Với \(m\) là tham số thực dương khác $1$. Hãy tìm tập nghiệm \(S\) của bất phương trình

\({\log _m}(2{x^2} + x + 3) \le {\log _m}(3{x^2} - x)\). Biết rằng \(x = 1\) là một nghiệm của bất phương trình.

Gọi $a$ là số thực lớn nhất để bất phương trình ${x^2} - x + 2 + a\ln \left( {{x^2} - x + 1} \right) \ge 0$ nghiệm đúng với mọi $x \in R.$ Mệnh đề nào sau đây đúng?

Tìm tập hợp nghiệm $S$ của bất phương trình: \({\log _{\frac{\pi }{4}}}({x^2} + 1) < {\log _{\frac{\pi }{4}}}(2x + 4)\)

Tập nghiệm của bất phương trình \({\log _{0,8}}\left( {{x^2} + x} \right) < {\log _{0,8}}\left( { - 2x + 4} \right)\) là:

Giải bất phương trình \({\log _{0,7}}\left( {{{\log }_6}\dfrac{{{x^2} + x}}{{x + 4}}} \right) < 0\)

Tập xác định của hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) là:

Tập hợp nghiệm của bất phương trình ${\log _{\frac{1}{3}}}\left( {{x^2} - 2x + 1} \right) < {\log _{\frac{1}{3}}}\left( {x - 1} \right)$ là:

Tập nghiệm của bất phương trình ${\log _{0,3}}x > {\log _{0,3}}3$ là:

Bất phương trình \({\log _4}\left( {{x^2} - 3x} \right) > {\log _2}\left( {9 - x} \right)\) có bao nhiêu nghiệm nguyên?

Xác định tập nghiệm $S$ của bất phương trình $\ln{x^2} > \ln\left( {4x - 4} \right)$

Tìm tập nghiệm S của bất phương trình ${\log _{x + 1}}\left( { - 2x} \right) > 2$

Tìm tập nghiệm S của bất phương trình \({\log _3}\left( {2x + 3} \right) < {\log _3}\left( {1 - x} \right)\)

Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}(x) > {\log _2}({x^2} - x) - 1$

Tập nghiệm của bất phương trình ${\log _2}\left( {{x^2} - 3x + 1} \right) \le 0$ là:

Tập nghiệm của bất phương trình \({\log _{\dfrac{1}{3}}}\left( {x - 1} \right) + {\log _3}\left( {11 - 2x} \right) \ge 0\) là

Tập nghiệm của phương trình \({\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1\) là

Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {{{\log }_4}\dfrac{{2x + 1}}{{x - 1}}} \right) > 1$

Giải bất phương trình: $\log _2^2x - 4033{\log _2}x + 4066272 \le 0$ .

Tập nghiệm của bất phương trình ${\log _2}x \le {\log _x}2$ là:

Tập nghiệm của bất phương trình ${\log _3}x \le {\log _{\frac{1}{3}}}(2x)$ là nửa khoảng $(a;b{\rm{]}}$. Giá trị của ${a^2} + {b^2}$ bằng

Tập nghiệm của bất phương trình ${\log _{\dfrac{1}{3}}}(x - 1) + {\log _3}(11 - 2x) \ge 0$ là

Tập nghiệm của bất phương trình $2017{\log _2}x \le {4^{{{\log }_2}9}}$ là

Tìm tập nghiệm S của bất phương trình $2{\log _3}\left( {4x - 7} \right) \le {\log _3}\left( {18x + 9} \right).$

Tập nghiệm của bất phương trình\({\log _2}\left( {x\sqrt {{x^2} + 2} + 4 - {x^2}} \right) + 2x + \sqrt {{x^2} + 2} \le 1\) là \(\left( { - \sqrt a ; - \sqrt b } \right]\). Khi đó \(ab\) bằng

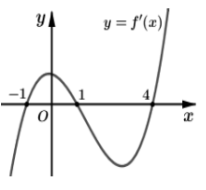
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị \(f'\left( x \right)\) như hình vẽ bên. Bất phương trình \({\log _5}\left[ {f\left( x \right) + m + 2} \right] + f\left( x \right) > 4 - m\) đúng với mọi \(x \in \left( { - 1;4} \right)\) khi và chỉ khi

× Close

báo lỗi

Vấn đề em gặp phải là gì? Đề bài sai Lời giải sai Lời giải khó hiểu Lỗi khác

Hãy viết chi tiết giúp Tự Học 365

Gửi Hủy bỏ

× Close

Note

Lưu note Hủy bỏ

×

Đăng ký

Năm sinh 20012002200320042005200620072008200920102011201220132014201520162017201820192020 hoặc Đăng nhập nhanh bằng: (*) Khi bấm vào đăng ký tài khoản, bạn chắc chắn đã đoc và đồng ý với Chính sách bảo mật và Điều khoản dịch vụ của Tự Học 365.