Biểu đồ Bode – Wikipedia Tiếng Việt

Trong kỹ thuật điện và điều khiển tự động, một biểu đồ Bode /'boʊdi/ là một đồ thị đáp ứng tần số của hệ thống. Nó thường là một kết hợp của một biểu đồ Bode biên độ, thể hiện biên độ của đáp ứng tần số, và một biểu đồ pha Bode, thể hiện sự lệch pha. Cả hai đại lượng trên được vẽ theo trục ngang tỉ lệ với logarit bậc 10 của tần số.

Đối với nhiều bài toán thực tế, các biểu đồ Bode chi tiết có thể xấp xỉ với các đoạn thẳng là tiệm cận của các đáp ứng chính xác. Hiệu quả của mỗi điều kiện của một hàm truyền nhiều yếu tố có thể được xấp xỉ bởi một tập hợp các đường thẳng trên biểu đồ Bode. Điều này cho phép một giải pháp đồ họa của hàm đáp ứng tần số tổng thể. Trước khi máy tính kỹ thuật số phổ biến, phương pháp đồ họa được sử dụng rộng rãi để làm giảm nhu cầu tính toán tẻ nhạt; một giải pháp đồ họa có thể được sử dụng để xác định phạm vi khả thi của các tham số cho một thiết kế mới.

Tổng quan

[sửa | sửa mã nguồn]

Trong nhiều đóng góp quan trọng của ông về lý thuyết mạch và lý thuyết điều khiển tự động, kỹ sư Hendrik Wade Bode, trong khi làm việc tại Bell Labs ở Mỹ trong những năm 1930, đã phát minh ra một phương pháp đơn giản nhưng chính xác để vẽ đồ thị độ lợi và độ dịch chuyển pha. Những biểu đồ này được mang tên ông, biểu đồ độ lợi Bode biểu đồ pha Bode. "Bode" được phát âm là /'boʊdi/ boh-dee (Hà Lan: ['boːdə]).[1][2]

Bode đã phải đối mặt với các vấn đề về thiết kế bộ khuếch đại ổn định với thông tin phản hồi để sử dụng trong các mạng điện thoại. Ông đã phát triển các kỹ thuật thiết kế đồ họa của biểu đồ Bode để hiển thị biên độ độ lợi và biên độ pha cần thiết để duy trì sự ổn định dưới sự biến đổi đặc tính mạch gây ra trong quá trình sản xuất hoặc trong quá trình hoạt động. [3] Các nguyên tắc phát triển đã được áp dụng để thiết kế các bài toán của cơ cấu servo và hệ thống điều khiển phản hồi khác. Biểu đồ Bode là một ví dụ về phân tích trong miền tần số.

Trục biên độ của biểu đồ Bode thường được biểu diễn theo decibel của công suất, bởi các quy tắc 20 log: 20 lần so với thông thường (cơ số 10) logarit của biên độ. Với biên độ theo logarit, biểu đồ Bode nhân với các biên độ đơn giản hóa việc thêm khoảng cách trên đồ thị (theo decibel), vì

Một biểu đồ Bode là một đồ thị của pha theo tần số, cũng được vẽ theo trục logarit của tần số, thường sử dụng trong liên kết với biểu đồ biên độ, để ước lượng một tín hiệu cần được dịch chuyển pha bao nhiêu. Ví dụ một tín hiệu được miêu tả bởi:  A sin ⁡ ( ω t ) {\displaystyle A\sin(\omega t)}  có thể bị suy giảm nhưng không dịch chuyển pha. Nếu hệ thống suy giảm nó bởi một hệ số x {\displaystyle x}  và dịch chuyển pha nó bởi  − Φ {\displaystyle -\Phi }  đầu ra tín hiệu của hệ thống sẽ là  ( A x ) sin ⁡ ( ω t − Φ ) {\displaystyle ({\frac {A}{x}})\sin(\omega t-\Phi )} . Dịch chuyển pha  Φ {\displaystyle \Phi }  thường là một hàm tần số.

Pha cũng có thể được thêm trực tiếp từ các giá trị đồ họa, một thực tế rõ ràng khi pha được xem là phần ảo của hàm phức logarit của một độ lợi phức.

Trong hình 1(a), các biểu đồ Bode được thể hiện cho hàm bộ lọc thông cao một cực:

Trong đó f là tần số theo Hz, và f1 là vị trí cực theo Hz, f1 = 100 Hz như trong hình. Sử dụng các quy tắc cho số phức, biên độ của hàm này là

và pha là:

Cần phải cẩn thận rằng các tiếp tuyến nghịch đảo được thiết lập để đưa về độ, chứ không phải là radian. Trên biểu đồ biên độ Bode, decibel được sử dụng, và độ lớn được vẻ là:

Trong hình 1(b), Các biểu đồ Bode dùng để thể hiện hàm bộ lọc thông thấp một cực:

Cũng thể hiện trong hình 1(a) và 1(b) là xấp xỉ tuyến tính để các biểu đồ Bode được sử dụng trong phân tích bằng tay, và được mô tả sau này.

Độ lớn và pha biểu đồ Bode hiếm khi có thể được thay đổi độc lập với nhau - thay đổi các đáp ứng biên độ của hệ thống sẽ thay đổi các đặc tính pha và ngược lại. Đối với hệ thống tối thiểu pha các đặc tính pha và biên độ có thể thu được qua lại với việc sử dụng biến đổi Hilbert.

Nếu hàm truyền là một hàm phân thức với các cực thực và zero, thì biểu đồ Bode có thể được xấp xỉ bằng các đường thẳng. Những xấp xỉ tiệm cận này được gọi là biểu đồ Bode đường thẳng hoặc biểu đồ Bode chưa được chỉnh sửa và rất hữu dụng bởi chúng có thể được vẽ bằng tay theo một vài quy tắc đơn giản. Các biểu đồ đơn giản thậm chí có thể được dự đoán mà không vẽ chúng.

Xấp xỉ này có thể được thực hiện bằng cách điều chỉnh giá trị ở mỗi tần số cắt. Biểu đồ được sau đó được gọi là một biểu đồ Bode đã chỉnh sửa.

Các quy tắc để vẻ biểu đồ Bode bằng tay

[sửa | sửa mã nguồn]

Những tiền đề của một biểu đồ Bode là người ta có thể xem xét một hàm theo công thức:

như là một tổng các logarit của các cực và zero của nó:

Ý tưởng này được sử dụng một cách rõ ràng trong phương pháp để vẽ sơ đồ pha. Phương pháp này để vẽ biểu đồ biên độ ngầm sử dụng ý tưởng này, nhưng do logarit của biên độ của mỗi cực hay zero luôn luôn bắt đầu từ zero và chỉ có một thay đổi tiệm cận (các đường thẳng), phương pháp này có thể được đơn giản hóa.

Biểu đồ biên độ tuyến tính hóa

[sửa | sửa mã nguồn]

Decibel biên độ thường được thực hiện bằng công thức d B = 20 log 10 ⁡ ( X ) {\displaystyle \mathbf {dB} =20\log _{10}(X)}  để định nghĩa. Một hàm truyền cho trước có dạng

trong đó  x n {\displaystyle x_{n}}  và  y n {\displaystyle y_{n}}  là các hằng số,  s = j ω {\displaystyle s=\mathrm {j} \omega } , a n , b n > 0 {\displaystyle a_{n},b_{n}>0} , và  H {\displaystyle H}  là hàm truyền:

• Tại mỗi giá trị của s trong đó ω = x n {\displaystyle \omega =x_{n}} (một zero), tăng độ dốc của đường thẳng bằng  20 ⋅ a n d B {\displaystyle 20\cdot a_{n}\,\mathrm {dB} }  trên mỗi decade.
• tại mỗi giá trị của s trong đó  ω = y n {\displaystyle \omega =y_{n}} (một cực), giảm độ dốc của đường thẳng bằng  20 ⋅ b n d B {\displaystyle 20\cdot b_{n}\,\mathrm {dB} }  trên mỗi decade.
• Giá trị ban đầu của đồ thị phụ thuộc vào các biên. Điểm đặt ban đầu được lập bằng cách đặt tần số góc ban đầu  ω {\displaystyle \omega }  vào hàm và tìm | H ( j ω ) | {\displaystyle |H(\mathrm {j} \omega )|} .
• Độ dốc ban đầu phụ thuộc vào số và bậc của zero và cực mà các giá trị bên dưới điểm ban đầu, và được tính bằng cách sử dụng hai nguyên tắc đầu tiên.

Để xử lý các đa thức bậc hai tối giản,  a x 2 + b x + c {\displaystyle ax^{2}+bx+c}  có thể, trong nhiều trường hợp, có thể xấp xỉ bằng  ( a x + c ) 2 {\displaystyle ({\sqrt {a}}x+{\sqrt {c}})^{2}} .

Lưu ý rằng các zero và cực xảy ra khi   ω {\displaystyle \omega }  bằng với một x n {\displaystyle x_{n}}  hoặc  y n {\displaystyle y_{n}}  xác định. Điều này là bởi hàm đang tìm là biên độ của  H ( j ω ) {\displaystyle H(\mathrm {j} \omega )} , và do nó là một hàm phức,  | H ( j ω ) | = H ⋅ H ∗ {\displaystyle |H(\mathrm {j} \omega )|={\sqrt {H\cdot H^{*}}}} . Vì vậy tại bất kỳ nơi nào mà có một zero hoặc cực bao gồm đơn thức  ( s + x n ) {\displaystyle (s+x_{n})} , biên độ của đơn thức đó là ( x n + j ω ) ⋅ ( x n − j ω ) = x n 2 + ω 2 {\displaystyle {\sqrt {(x_{n}+\mathrm {j} \omega )\cdot (x_{n}-\mathrm {j} \omega )}}={\sqrt {x_{n}^{2}+\omega ^{2}}}} .

Biểu đồ biên độ đã qua chỉnh sửa

[sửa | sửa mã nguồn]

Để chỉnh sửa một đồ thị biên độ tuyến tính hóa:

• Tại mỗi zero, đặt một điểm  3 ⋅ a n   d B {\displaystyle 3\cdot a_{n}\ \mathrm {dB} } trên đường thẳng,
• tại mỗi cực, đặt một điểm  3 ⋅ b n   d B {\displaystyle 3\cdot b_{n}\ \mathrm {dB} } dưới đường thẳng,
• vẽ một đường cong đi ngang qua những điểm này sử dụng các đoạn thẳng tiếp tuyến(các đoạn thẳng tiếp xúc đường cong).

Ghi chú rằng phương pháp điều chỉnh này không đi kèm với cách xử lý giá trị phức  x n {\displaystyle x_{n}}  hoặc  y n {\displaystyle y_{n}} . Trong trường hợp của một đa thức tối giản, cách tốt nhất để sửa đồ thị là tính toán thực sự biên độ của hàm truyền tại cực hoặc zero tương ứng với đa thức tối giản, và đánh dấu chấm trên hoặc dưới đường thẳng tại cực hoặc zero đó.

Biều đồ pha tuyến tính hóa

[sửa | sửa mã nguồn]

Cho trước một hàm truyền có cùng công thức như trên:

ý tưởng là vẽ các đồ thị riêng biệt cho mỗi cực và zero, sau đó chồng chúng lên. Các đồ thị pha thực tế được cho bởi  − arctan ⁡ ( I m [ H ( s ) ] R e [ H ( s ) ] ) {\displaystyle -\arctan \left({\tfrac {\mathrm {Im} [H(s)]}{\mathrm {Re} [H(s)]}}\right)} .

Để vẻ biểu đồ pha, với mỗi cực và zero:

• nếu A {\displaystyle A}  là dương, đường thẳng bắt đầu (với độ dốc bằng zero) tại  0 deg {\displaystyle 0\deg }
• nếu A là âm, đường thẳng bắt đầu (với độ dóc bằng zero) tại  180 deg {\displaystyle 180\deg }
• nếu tổng các số của các zero không ổn định và cực là lẻ, cộng 180 độ vào đó
• tại mỗi  ω = | x n | {\displaystyle \omega =|x_{n}|} (đối với các zero ổn định – Re ⁡ ( z ) < 0 {\displaystyle \operatorname {Re} (z)<0} ), tăng độ dốc lên  45 ⋅ a n {\displaystyle 45\cdot a_{n}}  độ trên mỗi decade, bắt đầu một decade trước ω = | x n | {\displaystyle \omega =|x_{n}|} (ví dụ: | x n | 10 {\displaystyle {\frac {|x_{n}|}{10}}} )
• Tại mỗi  ω = | y n | {\displaystyle \omega =|y_{n}|} (đối với các cực ổn định – Re ⁡ ( p ) < 0 {\displaystyle \operatorname {Re} (p)<0} ), giảm độ dốc xuống  45 ⋅ b n {\displaystyle 45\cdot b_{n}}  độ trên mỗi decade trước  ω = | y n | {\displaystyle \omega =|y_{n}|} (E.g.: | y n | 10 {\displaystyle {\frac {|y_{n}|}{10}}} )
• các cực và zero "không ổn định" (góc phần tư thứ nhất) ( Re ⁡ ( s ) > 0 {\displaystyle \operatorname {Re} (s)>0} ) có hành vi đối ngược nhau
• giảm độ dốc xuống khi pha thay đổi bởi  90 ⋅ a n {\displaystyle 90\cdot a_{n}}  độ (đối với một zero) hoặc  90 ⋅ b n {\displaystyle 90\cdot b_{n}}  độ (đối với một cực),
• Sau khi vẽ một đường thẳng cho mỗi cực hay zero, chồng các đường thẳng với nhau để có được biểu đồ pha cuối cùng; đó là, biểu đồ pha cuối cùng là xếp chồng của biểu đồ pha trước đó.

Ví dụ

[sửa | sửa mã nguồn]

Một bộ lọc RC thông thấp thụ động (độ lợi băng thông đơn vị), ví dụ có hàm truyền sau đây thể hiện trong miền tần số:

Từ hàm truyền ta có thể xác định được tần số cắt  f c {\displaystyle f_{\mathrm {c} }} (theo Hertz) là tại tần số

hoặc (tương đương) tại ω c = 1 R C {\displaystyle \omega _{\mathrm {c} }={1 \over {RC}}}  trong đó  ω c = 2 π f c {\displaystyle \omega _{\mathrm {c} }=2\mathrm {\pi } f_{\mathrm {c} }}  là tần số cắt góc theo radian trên giây.

Hàm truyền này viết theo tần số góc trở thành:

Phương trình trên là dạng chuẩn hóa của hàm truyền. Biểu đồ Bode được thể hiện trong hình 1(b) ở trên, và xây dựng đường thẳng xấp xỉ được thảo luận trong phần tiếp theo.

Biểu đồ biên độ

[sửa | sửa mã nguồn]

Biên độ (theo decibel) của hàm truyền ở trên (được chuẩn hóa và chuyển đổi sang dạng tần số góc), cho bởi biểu diễn độ lợi decibel  A v d B {\displaystyle A_{\mathrm {vdB} }} :

sau đó vẽ với tần số đầu vào ω {\displaystyle \omega }  trên một thang chia logarit, có thể được xấp xỉ bởi hai đường thẳng và nó tạo thành biểu đồ biên độ Bode tiếp tuyến (xấp xỉ) của hàm truyền đó:

• Đối với các tần số góc dưới  ω c {\displaystyle \omega _{\mathrm {c} }}  nó là một đường nằm ngang tại 0 dB vì tại các tần số thấp biểu thức  ω ω c {\displaystyle {\omega \over {\omega _{\mathrm {c} }}}}  rất nhỏ và có thể bỏ qua, làm cho phương trình độ lợi decibel ở trên bằng với zero,
• Đối với các tần số góc trên  ω c {\displaystyle \omega _{\mathrm {c} }}  nó là một đường thẳng với một độ dóc bằng −20 dB trên một decade vì tại các tần số cao biểu thức  ω ω c {\displaystyle {\omega \over {\omega _{\mathrm {c} }}}}  vượt lên trên và biểu thức độ lợi decibel ở trên được đơn giản bằng  − 20 log ⁡ ω ω c {\displaystyle -20\log {\omega \over {\omega _{\mathrm {c} }}}}  là một đường thẳng với độ dóc bằng  − 20 d B {\displaystyle -20\,\mathrm {dB} }  trên một decade.

Hai đường thẳng này gặp nhau ở tần số cắt. Từ biểu đồ này, có thể thấy rằng đối với các tần số thấp hơn tần số cắt, mạch điện có một sự suy giảm đến 0 dB, tương ứng với một độ lợi băng thông đơn vị, tức là biên độ của đầu ra bộ lọc bằng với biên độ của đầu vào. Tần số cao hơn tần số cắt đang suy yếu - tần số càng cao, độ suy giảm càng lớn.

Biểu đồ pha

[sửa | sửa mã nguồn]

Biểu đồ pha Bode được vẽ bằng góc pha của hàm truyền được cho bởi

đối với  ω {\displaystyle \omega } , trong đó  ω {\displaystyle \omega }  và  ω c {\displaystyle \omega _{\mathrm {c} }}  lần lượt là các tần số góc đầu vào cắt. Đối với các tần số đầu vào nhỏ hơn nhiều tần số cắt, tỉ số  ω ω c {\displaystyle {\omega \over {\omega _{\mathrm {c} }}}}  sẽ rất nhỏ và do đó góc pha sẽ gần với zero hơn. Khi tỉ số đó tăng thì giá trị tuyệt đối của pha sẽ tăng và trở thành –45 độ khi  ω = ω c {\displaystyle \omega =\omega _{\mathrm {c} }} . Khi tỉ số đó tăng đối với các tần số đầu vào lớn hơn nhiều so với tần số cắt, góc pha sẽ tiến gần tiệm cận −90 độ. Thang đo tần số cho biểu đồ pha được tính theo logarit.

Biểu đồ dạng chuẩn hóa

[sửa | sửa mã nguồn]

Trục tần số nằm ngang, ở cả biểu đồ pha và biểu đồ biên độ, có thể được thay bởi tỉ số tần số dạng chuẩn hóa (vô hướng)  ω ω c {\displaystyle {\omega \over {\omega _{\mathrm {c} }}}} . Trong trường hợp biểu đồ đó là dạng chuẩn hóa và các đơn vị của tần số không còn được dùng vì tất cả các tần số đầu vào bây giờ được biểu diễn là bội số của tần số cắt  ω c {\displaystyle \omega _{\mathrm {c} }} .

Một ví dụ với cực và zero

[sửa | sửa mã nguồn]

Hình 2-5 minh hoạ thêm cách dựng biểu đồ Bode. Ví dụ này với cả một cực và một zero cho thấy cách sử dụng xếp chồng như thế nào. Để bắt đầu, các thành phần được trình bày riêng.

Hình 2 cho thấy biểu đồ biên độ Bode cho một zero và một cực thông thấp, và so sánh hai biểu đồ đó với các biểu đồ Bode đường thẳng. Các biểu đồ Bode đường thẳng nằm ngang phía trên vị trí cực (zero) và sau đó giảm (tăng) ở 20 dB/decade. Thứ hai Hình 3 không giống nhau cho biểu đồ pha. Các biểu đồ pha đều nằm ngang so với một tần số là tích của 10 dưới vị trí cực (zero) và sau đó giảm (tăng) ở 45°/decade cho đến khi tần số đó bằng 10 lần so với vị trí cực (zero). Các biểu đồ sau đó là một lần nữa cuối cùng nằm ngang ở tần số cao hơn, tổng thay đổi pha bằng 90°.

Hình 4 và Hình 5 cho thấy làm thế nào để xếp chồng (thêm vào đơn giản) cho biểu đồ một cực và zero. Các biểu đồ Bode đường thẳng lại được so sánh với các biểu đồ chính xác. Zero đã được chuyển đến tần số cao hơn so với cực để thực hiện một ví dụ thú vị hơn. Lưu ý trong hình 4 là độ giảm 20 dB/decade của cực bị hãm bởi 20 dB/decade độ tăng của zero dẫn đến một biểu đồ biên độ nằm ngang với các tần số trên vị trí zero. Lưu ý trong hình 5 trong biểu đồ pha là đường thẳng xấp xỉ là gần đúng trong khu vực mà cả cực và zero đều ảnh hưởng đến pha. Cũng lưu ý trong hình 5 là dãi tần số mà pha thay đổi trong biểu đồ đường thẳng được giới hạn tới tần số là một tích số của mười ở trên và dưới vị trí cực (zero). Nơi pha của cực và zero đều có mặt, biểu đồ pha đường thẳng là nằm ngang vì độ dốc 45°/decade của cực bị hãm bởi độ tăng 45°/decade xếp chồng lên của zero trong phạm vi giới hạn của tần số nơi cả hai đều đóng góp tích cực vào pha.

• Example with pole and zero
• Figure 2: Biểu đồ biên độ Bode cho zero và cực thông thấp, đồ thị dược dán nhãn "Bode" là đồ thị Bode đường thẳng
• Figure 3: Biểu đồ pha Bode cho zero và cực thông thấp; đồ thị dán nhãn "Bode" là đồ thị Bode đường thẳng.
• Figure 4: Biểu đồ biên độ Bode cho cực-zero kết hợp; vị trí của zero cao hơn 10 lần trong hình 2&3; đồ thị được dán nhãn "Bode" là độ thị Bode đường thẳng
• Figure 5: đồ thị pha Bode cho cực-zero kết hợp; vị trí của zero cao gấp 10 lần trong hình 2&3; đồ thị dán nhãn "Bode" là đồ thị Bode đường thẳng.

Biên độ độ lợi và biên độ pha

[sửa | sửa mã nguồn]

Biểu đồ Bode được sử dụng để đánh giá sự ổn định của các bộ khuếch đại phản hồi âm bằng cách tìm độ lợi và biên độ pha của bộ khuếch đại. Khái niệm về độ lợi và biên độ pha được dựa trên biểu thức độ lợi cho một bộ khuếch đại phản hồi âm được cho bởi

Trong đó AFB là độ lợi của bộ khuếch đại với vòng phản hồi (độ lợi vòng kín), β là hệ số phản hồi và AOL độ lợi không phản hồi (độ lợi vòng hở). Độ lợi AOL là một hàm phức của tần số, với cả biên độ và pha.[note 1] Kiểm tra quan hệ này chỉ ra khả năng độ lợi vô cùng (nghĩa là không ổn định) nếu tích βAOL = −1. (Đó là, biên độ βAOL là đơn vị và pha của nó là −180°, được gọi là Tiêu chuẩn ổn định Barkhausen). Các biểu đồ Bode được sử dụng để xác định xem một bộ khuyết đại kín như thế nào để thỏa mãn điều kiện này.

Chìa khóa để xác định được điều này là 2 tần số. Đầu tiên, được ký hiệu là f180, là tần số mà độ lợi vòng hở đổi dấu. Thứ hai, được ký hiệu là f0 dB, là tần số mà biên độ của tích | β AOL | = 1 (theo dB, biên độ 1 là 0 dB). Do đó, tần số  f180 được xác định bởi điều kiện:

trong đó các trục dọc thể hiện biên độ của một số phức (ví dụ,   | a + j b | = [ a 2 + b 2 ] 1 2 {\displaystyle |a+\mathrm {j} b|=\left[a^{2}+b^{2}\right]^{\frac {1}{2}}} ), và tần số f0 dB được xác định bởi điều kiện:

Một biện pháp xấp xỉ đối với độ không ổn định là biên độ độ lợi. Biểu đồ pha Bode xác định tần số nơi mà pha của βAOL tiến tới −180°, thể hiện ở đây là tần số f180. Sử dụng tần số này, biểu đồ biên độ Bode tìm được biên độ của βAOL. Nếu |βAOL|180 = 1, bộ khuếch địa là không ổn định, như đã nói ở trên. Nếu |βAOL|180 < 1, bất ổn định sẽ không xảy ra, và khoảng cách theo dB của biên độ của |βAOL|180 với |βAOL| = 1 được gọi là biên độ đô lợi. Bởi vì độ lớn của một là 0 dB, biên độ độ lợi đơn giản là công thức tương đương: 20 log 10 ⁡ ( | β A O L | 180 ) = 20 log 10 ⁡ ( | A O L | 180 ) − 20 log 10 ⁡ ( β − 1 ) {\displaystyle 20\log _{10}(|\beta A_{\mathrm {OL} }|_{180})=20\log _{10}(|A_{\mathrm {OL} }|_{180})-20\log _{10}(\beta ^{-1})} .

Một biện pháp ước lượng xấp xỉ tương đương cho độ bất ổn định là biên độ pha. Biểu đồ biên độ Bode xác định tần số nơi biên độ của |βAOL| tiến tới bằng độ lợi của hàm đơn vị, thể hiện là tần số  f0 dB. Sử dụng tần số này, biểu đồ pha Bode tìm ra pha của βAOL. Nếu pha của  βAOL(f0 dB) > −180°, điều kiện bất ổn định không thể thỏa mãn tại bất kỳ tần số nào (bởi vì biên độ của nó sẽ < 1 khi f = f180), và khoảng cách của pha tại f0 dB theo độ trên −180° được gọi là biên độ pha.

Nếu vấn đề ổn định chỉ đơn giản là có hoặc không là tất cả những gì ta cần, bộ khuếch đại là ổn định nếu f0 dB < f180. Tiêu chuẩn này là đủ để dự đoán độ ổn định chỉ đối với các bộ khuếch địa thỏa mãn vài giới hạn trên vị trí cực và zero của chúng (các hệ thống cực tiểu pha). Mặc dù những giới hạn này thường được đáp ứng, nếu chúng không phải là biện pháp khác phải sử dụng, như biểu đồ Nyquist.[4][5] Độ lợi và biên độ pha tối ưu có thể được tính toán bằng cách sử dụng lý thuyết nội suy Nevanlinna–Pick.[6]

Các ví dụ sử dụng biểu đồ Bode

[sửa | sửa mã nguồn]

Hình 6 và 7 mô tả hành vi độ lợi và thuật ngữ. Đối với một bộ khuếch đại 3 cực, Hình 6 so sánh biểu đồ Bode cho độ lợi mà không cần phản hồi (độ lợi vòng hở) AOL với độ lợi phản hồi AFB (độ lợi vòng kín). Xem bộ khuếch đại phản hồi âm để biết thêm chi tiết.

Trong ví dụ này, AOL = 100 dB tại các tần số thấp, và 1 / β = 58 dB. Tại các tần số cao, AFB ≈ 58 dB.

Bởi vì độ lợi vòng hở AOL được vẽ và tích β AOLthì không, điều kiện AOL = 1 / β quyết định f0 dB. Độ lợi phản hồi tại các tần số thấp và đối với AOL lớn là AFB ≈ 1 / β (xem tại công thức cho độ lợi hồi tiếp tại phần đầu của bài này cho trường hợp độ lợi AOLlớn), vì vậy một cách để tìm ra f0 dB là tìm xem chỗ giao cắt độ lợi phản hồi với độ lợi vòng hở. (Tần số f0 dB cần thiết để tìm biên độ pha sau này.) 

Gần giao điểm của 2 độ lợi này tại f0 dB, tiêu chuẩn Barkhausen hầu như được thỏa mãn trong ví dụ này, và bộ khuếch đại phản hồi cho thấy một đỉnh độ lợi lớn (có lẽ là vô cùng nếu β AOL = −1). Tiến tới tần số độ lợi đơn vị f0 dB, độ lợi vòng hở đủ nhỏ là AFB ≈ AOL (kiểm tra công thức ở phần đầu của bài này cho trường hợp AOLnhỏ).

Hình 7 mô tả so sánh pha tương ứng: pha của bộ khuếch đại phản hồi thì gần như zero ra đến tần số f180 nơi độ lợi vòng hở có một pha là −180°. Trong vùng lân cận này, pha của bộ khuếch đại phản hồi giảm bất ngờ xuống gần như giống với pha của bộ khuếch đại phản vòng hở (Nhắc  lại, AFB ≈ AOL đối với AOLnhỏ.)

So sánh với các điểm ký hiệu trong hình 6 và hình 7, dường như tần số độ lợi đơn vị  f0 dB và tần số đảo pha f180 rất gần nhau trong bộ khuếch đại này, f180 ≈ f0 dB ≈ 3.332 kHz, nghĩa là biên độ độ lợi và biên độ pha gần như bằng zero. Bộ khuếch đại này là ổn định đường biên.

Hình 8 và hình 9 mô tả biên độ độ lợi và biên độ pha cho một lượng phản hồi khác β. Hệ số phản hồi được chọn nhỏ hơn trong hình 6 hoặc 7, di chuyển điều kiện | β AOL | = 1 tới tần số thấp hơn. Trong ví dụ này, 1 / β = 77 dB, và tại các tần số thấp hơn ta vẫn có AFB ≈ 77 dB.

Hình 8 hiển thị biểu đồ độ lợi. Từ hình 8, giao điểm của 1 / β và AOL xảy ra tại f0 dB = 1 kHz. Lưu ý rằng đỉnh của độ lợi AFB gần f0 dB gần như biến mất.[note 2][7]

Hình 9 là biểu đồ pha. Sử dụng giá trị của f0 dB = 1 kHz tìm thấy ở trên từ biểu đồ biên độ trong hình 8, pha vòng hở tại f0 dB là −135°, là một biên độ pha của 45° trên −180°.

Sử dụng hình 9, đối với một pha −180° giá trị của f180 = 3.332 kHz (kết quả tương tự được tìm thấy sớm hơn, tất nhiên[note 3]). Độ lợi vòng hở từ hình 8 tại f180 là 58 dB, và 1 / β = 77 dB, vì vậy biên độ độ lợi là 19 dB.

Độ ổn định không là tiêu chuẩn duy nhất cho độ jđápp ứng của bộ khuếch đại, và trong nhiều ứng dụng, một đòi hỏi khắt khe hơn độ ổn định là độ đáp ứng bước tốt. Là một quy tắc dựa trên kinh nghiệm, đáp ứng bước tốt yêu cầu một biên độ pha ít nhất là 45°, và thường xuyên chủ trương là biên độ vượt quá  70°, đặc biệt nơi biến thiên bộ phận theo dung sai sản xuất là một vấn đề.[7] Xem thêm tại thảo luận về biên độ pha trong bài đáp ứng bước.

• Examples
• = 1 xảy ra tại gần như f = f180°.
• = 1.
• Figure 8: Độ lợi của bộ khuếch đại phản hồi AFB theo dB và bộ khuếch đại vòng hở tương ứng AOL. Trong ví dụ này, 1 / β = 77 dB. Biên độ độ lơi trong bộ khuếch đại này là 19 dB.
• Figure 9: Pha của bộ khuếch đại phản hồi AFB theo độ và bộ khuếch đại vòng hở tương ứng AOL. Biên độ pha trong bộ khuếch đại này là 45°.

Chương trình/thiết bị vẽ biểu đồ Bode (Bode plotter)

[sửa | sửa mã nguồn]

Bode plotter là một thiết bị điện tử tương tự như một dao động ký, trong đó tạo ra một biểu đồ Bode, hoặc một đồ thị, của độ lợi điện áp hoặc độ dịch chuyển pha của một mạch điện theo tần số trong một hệ thống điều khiển phản hồi hoặc một bộ lọc. Một ví dụ của thiết bị này được thể hiện trong hình 10. Nó đặc biệt hữu dụng trong việc phân tích và kiểm trả các bộ lọc và độ ổn định của các hệ thống điều khiển phản hồi, thông qua việc đo lường các tần số cắt và độ lợi và biên độ pha.

Điều này giống hệt với chức năng được thực hiện bởi một thiết bị phân tích mạng vector, nhưng thiết bị phân tích mạng thường được sử dụng ở tần số cao hơn nhiều.

Đối với các mục đích giáo dục/nghiên cứu, vẽ biểu đồ Bode cho các hàm truyển giúp hiểu hơn và nhận được kết quả nhanh hơn (xem liên kết ngoài).

Các biểu đồ có liên quan

[sửa | sửa mã nguồn]

Hai biểu đồ liên quan hiển thị cùng một dữ liệu trong các hệ tọa độ khác nhau là biểu đồ Nyquist và biểu đồ Nichols. Đây là những biểu đồ tham số, với tần số là đầu vào và biên độ và pha của đáp ứng tần số là đầu ra. Biểu đồ Nyquist thể hiện những thông số đó trong hệ tọa độ cực, với biên độ ánh xạ theo bán kính và pha với argument (góc). Biểu đồ Nichols thể hiện những thông số này theo tọa độ hình chữ nhật, trên thang chia logarit.

• Related Plots
• Một biểu đồ Nyquist.
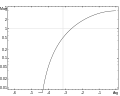• Một biểu đồ Nichols cùng đáp ứng.

Xem thêm

[sửa | sửa mã nguồn]

• Xử lý tín hiệu analog
• Biên độ pha
• Tích phân độ nhạy Bode
• Electrochemical impedance spectroscopy

Ghi chú

[sửa | sửa mã nguồn]

1. ^ Ordinarily, as frequency increases the magnitude of the gain drops and the phase becomes more negative, although these are only trends and may be reversed in particular frequency ranges.
2. ^ The critical amount of feedback where the peak in the gain just disappears altogether is the maximally flat or Butterworth design.
3. ^ The frequency where the open-loop gain flips sign f180 does not change with a change in feedback factor; it is a property of the open-loop gain.

Tham khảo

[sửa | sửa mã nguồn]

1. ^ Van Valkenburg, M. E. University of Illinois at Urbana-Champaign, "In memoriam: Hendrik W. Bode (1905-1982)", IEEE Transactions on Automatic Control, Vol.
2. ^ “Vertaling van postbode, NL>EN”. mijnwoordenboek.nl. Truy cập ngày 7 tháng 10 năm 2013.
3. ^ David A. Mindell Between Human and Machine: Feedback, Control, and Computing Before Cybernetics JHU Press, 2004 ISBN 0801880572, pp. 127-131
4. ^ Thomas H. Lee (2004). The design of CMOS radio-frequency integrated circuits . Cambridge UK: Cambridge University Press. tr. §14.6 pp. 451–453. ISBN 0-521-83539-9.
5. ^ William S Levine (1996). The control handbook: the electrical engineering handbook series . Boca Raton FL: CRC Press/IEEE Press. tr. §10.1 p. 163. ISBN 0-8493-8570-9.
6. ^ Allen Tannenbaum (1981). Invariance and Systems Theory: Algebraic and Geometric Aspects. New York, NY: Springer-Verlag. ISBN 9783540105657.
7. ^ a b Willy M C Sansen (2006). Analog design essentials. Dordrecht, The Netherlands: Springer. tr. 157–163. ISBN 0-387-25746-2.

Liên kết ngoài

[sửa | sửa mã nguồn]

• Explanation of Bode plots with movies and examples Lưu trữ 2005-04-23 tại Wayback Machine
• How to draw piecewise asymptotic Bode plots
• Summarized drawing rules Lưu trữ 2007-02-22 tại Wayback Machine (PDF)
• Bode plot applet - Accepts transfer function coefficients as input, and calculates magnitude and phase response
• Circuit analysis in electrochemistry
• Tim Green: Operational amplifier stability Lưu trữ 2012-02-13 tại Wayback Machine[1] Lưu trữ 2012-02-13 tại Wayback Machine Includes some Bode plot introduction
• Gnuplot code for generating Bode plot: DIN-A4 printing template (pdf)
• Hàm MATLAB để tạo một biểu đồ Bode của một hệ thống Lưu trữ 2017-04-05 tại Wayback Machine (tiếng Anh)
• MATLAB Tech Talk videos explaining Bode plots and showing how to use them for control design
• Insert the poles and zeros and this website will draw the asymptotic and accurate Bode plots
• Mathematica function for creating the Bode plot