Bồi Dưỡng HSG Toán 9 Chuyên đề 1: Hệ Thức Lượng Trong Tam Giác ...

Trang chủ » Hệ Thức Lượng Trong Tam Giác Vuông Nâng Cao 9 » Bồi Dưỡng HSG Toán 9 Chuyên đề 1: Hệ Thức Lượng Trong Tam Giác ...

Có thể bạn quan tâm

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông được VnDoc sưu tầm và đăng tải. Hy vọng với tài liệu này các bạn học sinh sẽ có thêm nhiều tài liệu ôn tập, củng cố thêm kiến thức, chuẩn bị tốt cho kì thi HSG và ôn thi vào lớp 10 sắp tới. Chúc các bạn học tốt, mời các bạn tham khảo.

Ngoài ra chúng tôi xin giới thiệu đến bạn đọc một số tài liệu hay và đặc sắc khác trong chương trình lớp 9:

  • Tổng hợp các chuyên đề bồi dưỡng học sinh giỏi lớp 9 môn Toán
  • Tổng hợp đề thi vào lớp 10 được tải nhiều nhất
  • Bộ đề thi vào lớp 10 môn Toán
  • 40 Đề thi Toán vào lớp 10 chọn lọc
  • Môn thi thứ tư vào lớp 10

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông

  • Chủ đề 1: Hệ thức về cạnh và đường cao trong tam giác vuông
  • Chủ đề 2: Tỉ số lượng giác của góc nhọn
  • Chủ đề 3: Hệ thức về góc và cạnh trong tam giác vuông

Chủ đề 1: Hệ thức về cạnh và đường cao trong tam giác vuông

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông

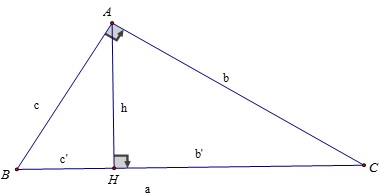
Cho ΔABC, góc A bằng 900, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:

+ BH = c' được gọi là hình chiếu của AB xuống BC

+ CH = b' được gọi là hình chiếu của AC xuống BC

Khi đó, ta có:

1) AB2 = BH.BC hay c2 = a.c'

AC2 = CH.BC hay b2 = a.b'

2) AH2 = CH.BH hay h2 = b'.c'

3) AB.AC = AH.BC hay b.c = a.h

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông

5) AB2 + AC2 = BC2 hay b2 + c2 = a2 (Định lý Pytago)

Ví dụ. Cho tam giác ABC vuông tại A , đường cao AH . Biết AB:AC = 3:4 và AB + AC = 21cm .

a) Tính các cạnh của tam giác ABC .

b) Tính độ dài các đoạn AH,BH,CH .

Hướng dẫn giải

Hình vẽ minh họa

a). Theo giả thiết: AB:AC = 3:4 ,

suy ra \frac{AB}{3} = \frac{AC}{4} = \frac{AB + AC}{3 + 4} = 3 .

Do đó AB = 3.3 = 9(cm) ; AC = 3.4 = 12(cm) .

Tam giác ABC vuông tại A , theo định lý Pythagore ta có:

BC^{2} = AB^{2} + AC^{2} = 9^{2} + 12^{2} = 225 , suy ra BC = 15cm .

b) Tam giác ABC vuông tại A , ta có AH.BC = AB.AC , suy ra AH = \frac{AB.AC}{BC} = \frac{9.12}{15} = 7,2(cm) .

AH^{2} = BH.HC .

Đặt BH = x(0 < x < 9) thì HC = 15 - x , ta có:

(7,2)^{2} = x(15 - x) \Leftrightarrow x^{2} - 15x + 51,84 = 0

\Leftrightarrow x(x - 5,4) = 9,6(x - 5,4) = 0

\Leftrightarrow (x - 5,4)(x - 9,6) = 0 \Leftrightarrow x = 5,4 hoặc x = 9,6 (loại)

Vậy BH = 5,4cm . Từ đó HC = BC - BH = 9,6(cm) .

Chú ý: Có thể tính BH như sau:

AB^{2} = BH.BC suy ra BH = \frac{AB^{2}}{BC} = \frac{9^{2}}{15} = 5,4(cm) .

Chủ đề 2: Tỉ số lượng giác của góc nhọn

1. Định nghĩa

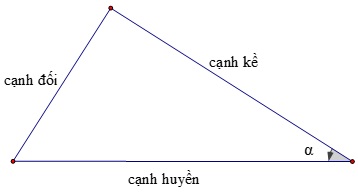
Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông

2. Định lí

Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.

3. Một số hệ thức cơ bản

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông

4. So sánh các tỉ số lượng giác

a) Cho α,β là hai góc nhọn. Nếu α < β thì

* sinα < sinβ; tanα < tanβ

*cosα > cosβ; cotα > cotβ

b) sinα < tanα; cosα < cotα

Ví dụ: Cho tam giác ABC với các đỉnh A,B,C và các cạnh đối diện với các đỉnh tương ứng là: a,b,c .

a. Tính diện tích tam giác ABC theo a

b. Chứng minh: a^{2} + b^{2} + c^{2} \geq 4\sqrt{3}S

Hướng dẫn giải

Hình vẽ minh họa

a) Ta giả sử góc A là góc lớn nhất của tam giác ABC \Rightarrow B,C là các góc nhọn.

Suy ra chân đường cao hạ từ A lên BC là điểm H thuộc cạnh BC .

Ta có: BC = BH + HC . Áp dụng định lý

Pi ta go cho các tam giác vuông AHB,AHC ta có:

AB^{2} = AH^{2} + HB^{2},AC^{2} = AH^{2} + HC^{2}

Trừ hai đẳng thức trên ta có:

c^{2} - b^{2} = HB^{2} - HC^{2}

= (HB +HC)(HB - HC) = a.(HB - HC)

\Rightarrow HB - HC = \frac{c^{2} - b^{2}}{a} ta cũng có: HB + HC = a \Rightarrow BH = \frac{a^{2} + c^{2} - b^{2}}{2a} .

Áp dụng định lý Pitago cho tam giác vuông AH B

\Rightarrow AH^{2} = c^{2} - \left(\frac{a^{2} + c^{2} - b^{2}}{2a} \right)^{2}

= \left( c - \frac{a^{2} +c^{2} - b^{2}}{2a} \right)\left( c + \frac{a^{2} + c^{2} - b^{2}}{2a}\right)

= \left\lbrack \frac{(a + c)^{2} - b^{2}}{2a}\right\rbrack.\left\lbrack \frac{b^{2} - (a - c)^{2}}{2a} \right\rbrack

= \frac{(a + b + c)(a + c - b)(b + a - c)(b + c -a)}{4a^{2}}

Đặt 2p = a + b + c thì AH^{2} = \frac{16p(p - a)(p - b)(p - c)}{4a^{2}}

\Rightarrow AH = 2\frac{\sqrt{p(p - a)(p - b)(p - c)}}{a} .

Từ đó tính được S = \frac{1}{2}BC.AH = \sqrt{p(p - a)(p - b)(p - c)}

b). Từ câu a) ta có: S = \sqrt{p(p - a)(p - b)(p - c)} .

Áp dụng bất đẳng thức Cô si ta có:

(p - a)(p - b)(p - c) \leq \left( \frac{p - a + p - b + p - c}{3} \right)^{3} = \frac{p^{3}}{27} .

Suy ra S \leq \sqrt{p.\frac{p^{3}}{27}} = \frac{p^{2}}{3\sqrt{3}} . Hay S \leq \frac{(a + b + c)^{2}}{12\sqrt{3}} .

Mặt khác ta dễ chứng minh được: (a + b + c)^{2} \leq 3\left( a^{2} + b^{2} + c^{2} \right)

Suy ra S \leq \frac{3\left( a^{2} + b^{2} + c^{2} \right)}{12\sqrt{3}} \Leftrightarrow a^{2} + b^{2} + c^{2} \geq 4\sqrt{3}S

Dấu bằng xảy ra khi và chỉ khi tam giác ABC đều.

Chủ đề 3: Hệ thức về góc và cạnh trong tam giác vuông

1. Các hệ thức

Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề

b) Cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề

 

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông

b = a.sinB = a.cosC

c = a.sinC = a.cosB

b = c.tanB = c.cotC

c = b.tanB = b.cotC

Ví dụ. Biết \sin\alpha = \frac{5}{13} . Tính \cos\alpha,tan\alpha và \cot\alpha .

Hướng dẫn giải

Cách 1. Xét \Delta ABC vuông tại A .

Đặt \widehat{B} = \alpha . Ta có: \sin\alpha = \frac{AC}{BC} = \frac{5}{13}

suy ra \frac{AC}{5} = \frac{BC}{13} = k , do đó: AC = 5k,BC = 13k .

Tam giác ABC vuông tại A nên:

AB^{2} = BC^{2} - AC^{2} = (13k)^{2} - (5k)^{2} = 144k^{2} , suy ra AB = 12k .

Vậy \cos\alpha = \frac{AB}{BC} = \frac{12k}{13k} = \frac{12}{13} ; \tan\alpha = \frac{AC}{AB} = \frac{5k}{12k} =\frac{5}{12};cot\alpha = \frac{AB}{AC} = \frac{12k}{5k} =\frac{12}{5}

Cách 2. Ta có \sin\alpha = \frac{5}{13} suy ra sin^{2}\alpha = \frac{25}{169} , mà sin^{2}\alpha + cos^{2}\alpha = 1

Do đó cos^{2}\alpha = 1 - sin^{2}\alpha = 1 - \frac{25}{169} = \frac{144}{169} , suy ra \cos\alpha = \frac{12}{13} .

\tan\alpha = \frac{\sin\alpha}{\cos\alpha} = \frac{5}{13}:\frac{12}{13} = \frac{5}{13}.\frac{13}{12} = \frac{5}{12} ; \cot\alpha = \frac{\cos\alpha}{\sin\alpha} = \frac{12}{13}:\frac{5}{13} = \frac{12}{13}.\frac{13}{5} = \frac{12}{5} .

Ở cách giải thứ nhất ta biểu thị độ dài các cạnh của tam giác ABC theo đại lượng k rồi sử dụng định nghĩa tỉ số lượng giác của góc nhọn để tính \cos\alpha,tan\alpha,cot\alpha . Ở cách giải thứ hai, ta sử dụng giả thiết \sin\alpha = \frac{5}{13} để tính sin^{2}\alpha rồi tính \cos\alpha từ sin^{2}\alpha + cos^{2}\alpha = 1 . Sau đó ta tính \tan\alpha và \cot\alpha qua \sin\alpha và \cos\alpha .

2. Giải tam giác vuông

Là tìm tất cả các yếu tố còn lại của một tam giác vuông khi biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông)

Ví dụ. Cho tam giác ABC có AB = 16,AC = 14 và \widehat{B} = 60^{0}.

a) Tính độ dài cạnh BC.

b) Tính diện tích tam giác ABC.

Hướng dẫn giải

Hình vẽ minh họa

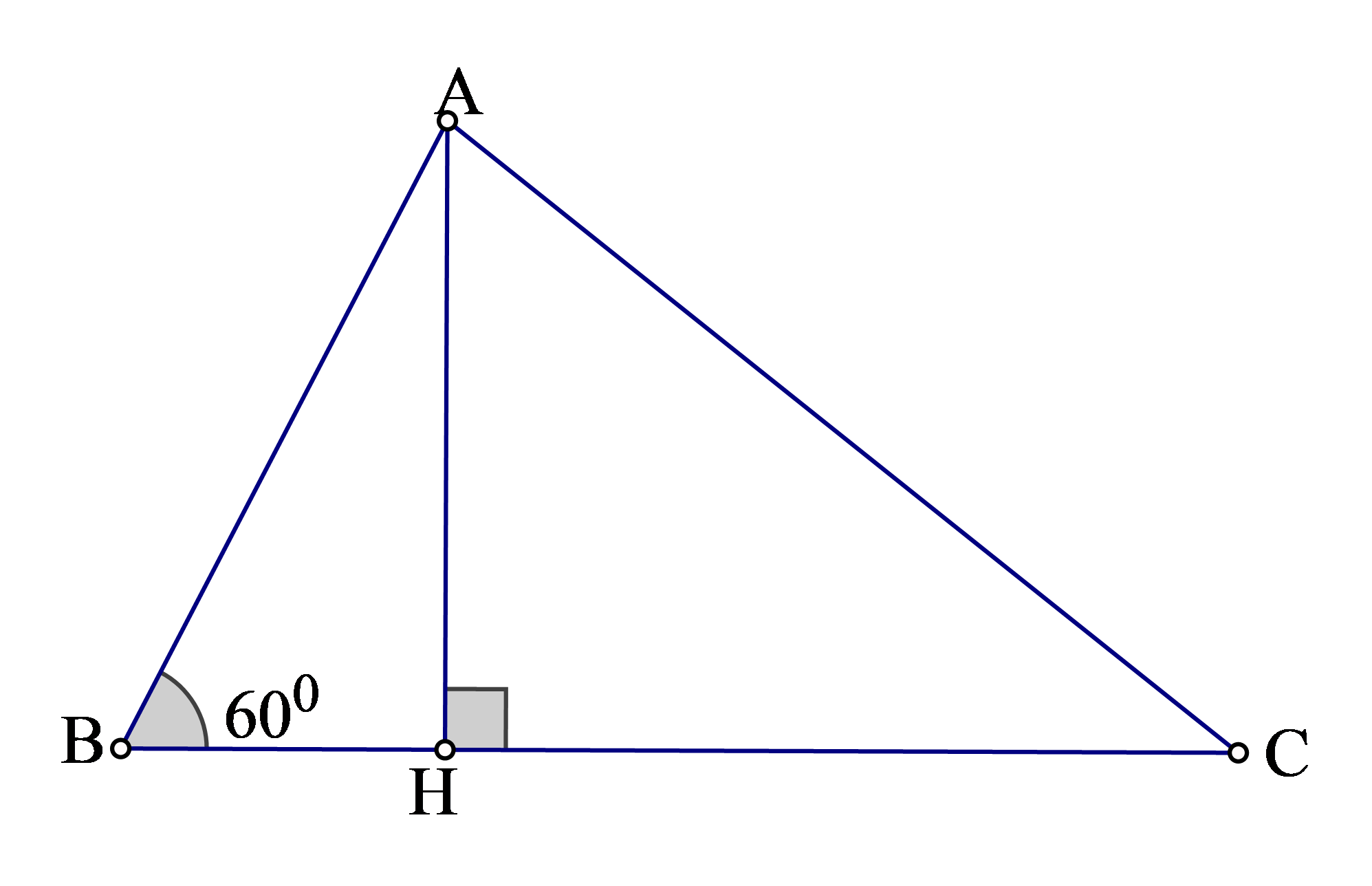
a) Kẻ đường cao AH.

Xét tam giác vuông ABH, ta có:

BH = AB.cosB = AB.cos60^{0} = 16.\frac{1}{2} = 8

AH = AB.sinB = AB.sin60^{0} = 16.\frac{\sqrt{3}}{2} = 8\sqrt{3}.

Áp dụng định lý Pythagore vào tam giác vuông AHC ta có:

HC^{2} = AC^{2} - AH^{2} = 14^{2} - \left( 8\sqrt{3} \right)^{2} = 196 - 192 = 4.

Suy ra HC = 2.

Vậy BC = CH + HB = 2 + 8 = 10.

b) Cách 1. S_{ABC} = \frac{1}{2}BC.AH = \frac{1}{2}.10.8\sqrt{3} = 40\sqrt{3} (đvdt)

Cách 2. S_{ABC} = \frac{1}{2}BC.BA.sinB = \frac{1}{2}.10.16.\frac{\sqrt{3}}{2} = 40\sqrt{3} (đvdt)

----------------------------------------------------------------------

Mời các bạn làm bài tập nâng cao: Bồi dưỡng HSG Toán 9: Bài tập nâng cao chuyên đề 1

Bồi dưỡng HSG Toán 9 chuyên đề 1: Hệ thức lượng trong tam giác vuông được VnDoc đã chia sẻ trên đây. Khi giải các bài toán liên quan đến cạnh và đường cao trong tam giác vuông, ngoài việc nắm vững các kiến thức về định lý Talet chúng ta cần nắm thêm về các trường hợp đồng dạng của tam giác từ đó chuẩn bị tốt cho kì thi HSG lớp 9 sắp tới. Chúc các bạn học tốt, mời các bạn tham khảo

  • Chủ đề 1: Căn bậc hai và các bài toán liên quan
  • Chủ đề 2: Bất đẳng thức
  • Chủ đề 3: Phương trình
  • Chủ đề 4: Hàm số bậc nhất - hàm số bậc hai
  • 8 Chuyên đề Toán nâng cao ôn thi lớp 10 và thi học sinh giỏi lớp 9
  • Bồi dưỡng HSG Toán 9 chuyên đề 2: Đường tròn

Từ khóa » Hệ Thức Lượng Trong Tam Giác Vuông Nâng Cao 9